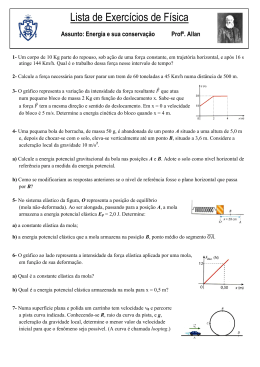
PROVA G2 FIS 1026 – 07/10/2010
MEC•NICA NEWTONIANA B
Gabarito
NOME:_______________________________
No:_________
TURMA:_______
QUEST‚O
VALOR
1
4,0
2
3,0
3
3,0
TOTAL
10,0
GRAU
REVIS‚O
Dados:
g = 10,0 m/s 2 = 1000 cm/s2
K = ƒ m v 2; W = ∫ F . ds;
W total = ΔK;
p = mv;
W cons = - ΔU;
Fmed = ΔP / Δt;
Wmola = ƒ k xi2 - ƒ k xf2
 F ext = Macm ;
Mvcm =  pi;
Rcm =  mi ri /  mi
∫ Asn ds = A s(n+1)/ (n+1)
Col. el†stica: Pa = Pd e K1a + K2a = K1d + K2d ou v 1a - v 2a = -(v 1d - v 2d)
Col. el†stica unidimensional:
Obs.: os cÄlculos devem ser feitos com 2 nÅmeros significativos
A duraÇÉo da prova Ñ de 1 hora e 50 minutos.
Respostas sem justificativa nÉo serÉo computadas.
Esta prova tem 4 folhas, contando com a capa. Confira.
1
(1a questão - 4,0 pontos) A pista de
obst†culos mostrada na figura ser†
percorrida por um carro de massa
m = 100 kg. Os planos inclinados s‡o
idˆnticos, formam o ‰ngulo de 45o
m
10
com a horizontal e tˆm comprimentos
totais OB = CD = 20 m. A forŠa
m
10
vari†vel F(s) = Fo[s(10 – s)+1] (N) ‹
paralela ao plano inclinado e atua
entre os pontos O e A (OA = 10 m),
empurrando o carro para cima a partir do repouso na origem O. Na equaŠ‡o que define
a forŠa, s ‹ a dist‰ncia medida ao longo do plano inclinado a partir da origem O
(0 m ≤ s ≤10 m).
a) Determine o trabalho realizado pela forŠa sobre o carro no intervalo OA em funŠ‡o
do par‰metro Fo.
J
b) Sabendo que o carro atinge o ponto B com velocidade de m•dulo vB = 20 m/s e que
n‡o existe atrito no trecho OB, determine o valor do par‰metro Fo, usando conceitos de
energia.
Como a variaŠ‡o da energia mec‰nica do sistema (carro) entre os pontos O (inicial) e B
(final) ‹ igual ao trabalho W F, tem-se
Como
fornece
,
,
e W F foi calculado em (a), a equaŠ‡o acima
c) Determine o valor da dist‰ncia X para que, ap•s se deslocar no ar no trecho BC, o
carro tenha vetor velocidade tangente ao segundo plano inclinado no ponto C.
O carro se movimenta como um proj‹til no ar entre os pontos B e C, conservando sua
energia mec‰nica. Como os pontos B e C tˆm a mesma altura (hC = hB ) e a velocidade
horizontal de um proj‹til ‹ constante (v Cx = vBx), tem-se
Portanto v C = vB = 20 m/s (em m•dulo) e vCy = - v By . Como vCy = vBy – gt, tem-se
Finalmente
d) Sabe-se que o coeficiente de atrito cin‹tico entre o trecho CDE da pista e o carro ‹
 c = 0,5 e deseja-se que o carro percorra 20 m no trecho horizontal DE da pista at‹
parar, comprimindo a mola ideal de 1 m. Determine o valor da constante el†stica da
mola, usando conceitos de energia.
2
Como a variaŠ‡o da energia mec‰nica do sistema (carro+mola) entre os pontos B
(inicial) e E (final) se deve ao atrito no trecho CDE, tem-se
Como
,
,
e
, a equaŠ‡o acima fornece
N/m
(2a questÉo - 3,0 pontos) a) Um biscoito de massa M se movimenta numa mesa
horizontal sem atrito, numa trajet•ria retilŽnea com velocidade V = 3i+4j (m/s).
Repentinamente o biscoito explode em dois pedaŠos: um de massa m1=0,3 M e outro
de massa m2=0,7 M. Logo ap•s a explos‡o, o pedaŠo de massa m1 se movimenta com
velocidade v 1 = -3i+4j (m/s). Calcule o vetor velocidade v2 da massa m2.
ConservaŠ‡o do momento linear: MV = m1v 1 + m2v 2.
Ent‡o: M(3i+4j) = 0,3M(-3i+4j)+0,7Mv 2  (3i+4j)=(-0,9i+1,2j)+0,7v 2 
v 2 = [3,9i+2,8j]/0,7 = 5,57i+4j (m/s)
b) Duas bolas de chiclete batem numa colis‡o perfeitamente inel†stica, formando uma
bolota de chiclete de massa M. As velocidades antes da colis‡o s‡o v1 = 1i+1j (m/s) e
v 2 = -2i-5j (m/s). Ap•s a colis‡o a velocidade da bolota ‹ V = -1i-3j (m/s). Calcule os
quocientes m1/M e m2/M.
ConservaŠ‡o do momento linear: m1v 1 + m2v 2 = MV
Por componentes: eixo X  m1 – 2m2 = -M ; eixo Y  m1 - 5m2 = -3M
Assim, subtraindo X – Y teremos: 3m2 = 2M  m2/M = 2/3. Substituindo em X ou Y ou
lembrando que m1 + m2 = M teremos que m1/M = 1/3.
c) Duas bolas de sinuca colidem elasticamente. Elas se movimentam numa mesa
horizontal sem atrito. As duas bolas tˆm massas iguais. As velocidades antes da
colis‡o s‡o v 1a = 1,4142i (m/s) e v 2a = 1,00j (m/s). Logo depois da colis‡o a velocidade
da bola 1 ‹ v1d = 0,4142i + 1,31j. Calcule o vetor velocidade v2d da bola 2 e a energia
cin‹tica Kd do sistema logo depois da colis‡o. Assuma a massa de cada bola igual a
200 g.
ConservaŠ‡o do momento linear: m1 v1a + m2 v2a = m1 v1d + m2 v2d
ConservaŠ‡o da energia cin‹tica: ƒ m1v 1a2 + ƒ m2v 2a2 = ƒ m1v 1d2 + ƒ m2v 2d2
x: 1,4142 i = 0,4142 i + v2dx  v 2dx = 1i y: 1 j = 1,31 j + v 2dy  v 2dy = -0,31 j
v 2d = (1i-0,31j) m/s
Ka = Kd = ƒ m1v 1a2 + ƒ m2v 2a2 = 0,3 J.
3
(3a questÉo - 3,0 pontos) Considere o trilho sem atrito mostrado na figura abaixo.
A
m1
H =5,0m
=,05,0m
L
0
m2
θ
B
Um bloco de massa m1 = 5,0 kg ‹ solto com velocidade inicial de 36 km/h no ponto A.
No ponto B ele colide elasticamente com o bloco de massa m2 = 104 g. O bloco de
massa m2 percorre o trilho e alcanŠa uma rampa de inclinaŠ‡o θ = 30o e comprimento L
at‹ uma mola relaxada de constante el†stica k = 1,0 N/cm. Observe atentamente as
unidades nos campos de resposta e determine:
a) A altura m†xima h alcanŠada pelo bloco de massa m1 AP•S a colis‡o.
4
b) O comprimento mŽnimo L da rampa para que o bloco de massa m2 n‡o alcance a
mola.
c) Se L = 500 cm, determine a compress‡o m†xima da mola.
5