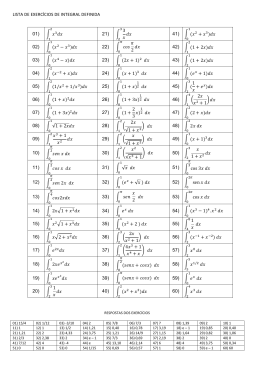
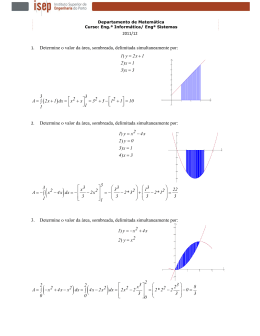
Integrais Imediatos – (a,b,c são constantes)
x6
x2
x6
+ 4 + 8x + C = + 2x 2 + 8x + C
6
2
2
1)
5
5
∫ (3x + 4x + 8)dx = 3∫ x dx + 4 ∫ xdx + ∫ 8dx = 3
2)
dx
x −3+1
x −2
1
−3
=
x
dx
=
+
C
=
+C = − 2 +C
∫ x3 ∫
−3 + 1
−2
2x
3)
4
4
∫ ax dx = a ∫ x dx = a
x 4 +1
1
+ C = ax 5 + C
4 +1
5
4)
 2a b

− 2 + 3c  dx =
x x

∫ 
∫
2a
b
1
dx + ∫ − 2 dx + ∫ 3c dx = 2a ∫ dx − b ∫ x −2 dx + 3c ∫ 1dx
x
x
x
= 2a ln x − b
x −2 +1
b
+ 3cx + C = 2a ln x + + 3cx + C
−2 + 1
x
5)
∫ (5x − 2)
235
1
1 (5x − 2) 235 +1
(5x − 2)236
235
dx = ∫ 5(5x − 2) dx =
+C =
+C
5
5 ( 235 + 1)
1180
u = 5x − 2
u'= 5
6)
10
∫ (8x + 3) dx =
1
(8x + 3)11
10
8
(
8x
+
3
)
dx
=
+C
8∫
88
u = 8x + 3
u'= 8
7)
3
2
6
3
∫ (2x − 4) dx = ∫ (4x − 16 x + 16 )dx =
8)
25
∫ (6 x − 2) dx =
9)
2
∫ (x +
4x7
− 4x 4 + 16 x + C
7
1
(6 x − 2) 26
25
6
(
6
x
−
2
)
dx
=
+C
6∫
156
1
x3 1
2
−2
)
dx
=
(
x
+
x
)
dx
=
− +C
∫
x2
3 x
1 +1
− 1 +1
3
1
1
1
x 2
x 2
x 2 x 2
2 3
−1
10) ∫ ( x +
)dx = ∫ ( x 2 + x 2 )dx =
+
+C =
+
+C =
x +2 x +C
3
1
1 +1
3
x
− 1 +1
2
2
2
2
(
2 + 5x dx = ∫ ( 2 + 5x ) 2 dx =
1
11)
∫
12)
∫t
13)
∫ (1 − x)
14)
∫ (2t
2
) (
)
1
1
2
5 ( 2 + 5x ) 2 dx =
(2 + 5x)3 + C
∫
5
15
2
dt = 2 ∫ t −2 dt = − + C
t
2
x dx = ∫ ( x − x x ) dx = ∫ ( x
+ 1) 2 dt = ∫ (4t 4 + 4t 2 + 1) dt =
2
1
2
3
− x 2 ) dx =
2 3 2 5
x −
x +C
3
5
4 5 4 3
t + t +t +C
5
3
15)
(
)
− x2
( −3 )
x3 − x2 − 3
x3
−2
dx
=
+
∫ x2
∫ x 2 x 2 + x 2 dx = ∫ x − 1 − 3x dx =
x2
x −1
x2
1
x 3 − 2x 2 + 6
= − x−3
+C = − x+3 +C =
+C
2
−1
2
x
2x
16)
17)
x 3 + 5x 2 − 4
4
x3 + 10x 2 + 8
dx
=
x
+
5
−
dx
=
+C
∫ x2
∫
x2
2x
∫
t3
a +t
4
(
dt = ∫ t 3 a 4 + t 4
4
)
−1
dt =
2
(
1
4t 3 a 4 + t 4
∫
4
)
−1
2
dt =
1 4 4
a +t +C
2
18)
2
∫
2
( a 3 − x 3 )3
x
2
3
1
3
u=a −x
−
1
2
2
dx = ∫ x 3 (a 3 − x 3 )3 dx = −
2
2
3
2 − 31 23
3 23
3 3
3 4
−
x
(
a
−
x
)
dx
=
−
(
a
−
x
) +C
∫
2
3
8
2
3
2
1
2 −1
2 −
u ' = − x3 = − x 3
3
3
19)
∫ 3ay dy = a ∫ 3 y dy = ay
20)
∫
2
2
3
+C
axdx = ∫ a xdx = a ∫ xdx =
2x ax
+C
3
3
1
1
1 1
1
2
2
21) ∫ ( 2x +
)dx = ∫ ( 2 x +
)dx = (2x) + (2x) + C
3
2x
2 x
22)
3x
∫
1− x
2
(
dx = 3 ∫ x 1 − x 2
)
1
2
dx = 3
(
1
−2x 1 − x 2
∫
−2
)
1
2
dx = − 3 1 − x 2 + C
(a + bt )2
1
11
(a + bt )3
2
2
23) ∫
dt = ∫ (a + bt ) dt =
b(a + bt ) dt =
+C
2
2
2b∫
6b
24)
( a − x )2
1 1
2
dx = −2 ∫ −
( a − x ) 2 dx = − ( a − x )3 + C
∫
2 x
3
x
u= a− x = a−x
1
2
1 −1
1
u'= − x 2 = −
2
2 x
25)
(
∫
)
x (3x − 2)dx = ∫ 3x x − 2 x dx =
6 52 4 32
x − x +C
5
3
26)
3
−
2
3
2
1
−
1
1
2
3
3
∫ t (1 + 2t ) dt = 6 ∫ 6t (1 + 2t ) 3 dt = 2 (1 + 2t ) 3 + C
u = 1 + 2t 3
2
u ' = 6t 2
27)
∫(
28)
∫
3
a − x ) 2 dx = ∫ (a − 2 a x + x)dx = ax −
(
1 − x 2 x dx = ∫ x 1 − x 2
)
1
3
dx =
4
1
x ax + x 2 + C
3
2
(
1
−2x 1 − x 2
−2 ∫
)
1
3
4
3
dx = − (1 − x 2 ) 3 + C
8
29)
∫
x ( a − x ) 2 dx = ∫ x (a − 2 a x + x)dx = ∫ (a x − 2 ax + x x )dx =
=
2 32
2 5
ax − x 2 a + x 2 + C
3
5
30)
x2 + 1
∫
x 3 + 3x
(
)(
dx = ∫ x 2 + 1 x 3 + 3x
=
(
)
−1
)(
2
1
3x 2 + 3 x 3 + 3x
∫
3
dx =
)
−1
2
(
)(
)
1
1
3 x 2 + 1 x 3 + 3x − 2 dx =
∫
3
dx =
2 3
x + 3x + C
3
u = x 3 + 3x
u ' = 3x 2 + 3
31)
2 + ln x
1
1
ln 2 x
dx
=
2
dx
+
xdx
=
=
2
x
+
+C
ln
ln
∫ x
∫x ∫x
2
u = ln x
1
x
u'=
−
3
32)
2
2 2
∫ (a + b x ) 2 x dx =
33)
∫ (2t
2
3
−
1
1
2
2
2 2
2
2b
x
(
a
+
b
x
)
dx = −
+C
2 ∫
2b
b2 a 2 + b2 x 2
+ 1) 2 dt = ∫ (4t 4 + 4t 2 + 1)dt =
4 5 4 3
t + t +t +C
5
3
1
1 a6 x
a6 x
6x
34) ∫ a dx = ∫ 6a dx =
+C =
+C
6
6 ln a
ln a6
6x
35)
∫ (e
x
+ 1)3 e x dx = ∫ e x (e x + 1)3 dx =
1 x
(e + 1)4 + C
4
u = ex + 1
u ' = ex
36)
2x
∫ 2 dx =
1
1 22 x
22 x
2x
2
2
dx
=
+
C
=
+C
2∫
2 ln 2
ln 4
( )
37)
1
1
a 3 x −6 x
3 x 2 −6 x
3 x 2 −6 x
∫ a ( x − 1) dx = 6 ∫ 6 ( x − 1) a dx = 6 ∫ (6 x − 6 ) a dx = 6 ln a + C
u = 3x 2 − 6 x
u ' = 6x −6
2
3 x 2 −6 x
38)
∫e
4x
dx =
1
1
4e4 x dx = e4 x + C
∫
4
4
39)
∫e
5 x2
xdx =
2
2
1
1
10xe5 x dx = e5 x + C
∫
10
10
40)
2x
dx = ln( x 2 + 3) + C
+3
u = x2 + 3
u ' = 2x
∫x
2
41)
∫ 4x
x
2
+1
dx =
(
)
(
1
8x
1
dx = ln 4x 2 + 1 + C = ln  4x 2 + 1
2
∫
8 4x + 1
8

)
1
8
 + C = ln 8 4x 2 + 1 + C


u = 4x 2 + 1
u ' = 8x
42)
x2
1
9x 2
1
dx
=
dx = ln(3x 3 + 4) + C
3
∫ 3x3 + 4
∫
9 3x + 4
9
3
u = 3x + 4
u ' = 9x 2
43)
(
)
x
1
2x
1
dx = ∫ 2
dx = ln x 2 + 4 + C = ln x 2 + 4 + C
+4
2 x +4
2
2
u = x +4
∫x
2
u ' = 2x
ex
1
be x
1
44) ∫
dx = ∫
dx = ln(a + be x ) + C
x
x
a + be
b a + be
b
45)
x+2
∫ x + 1 dx = ∫
x +1+1
x +1
1
1
dx = ∫
+
dx = ∫ 1 +
dx = x + ln( x + 1) + C
x +1
x +1 x+1
x +1
46)
3
5
x+
x+4
1 x+4
1
1
5 1
∫ 2x + 3 dx = 2 ∫ 3 dx = 2 ∫ 32 + 2 3 dx = 2 ∫ 1 + 2 3 dx =
x+
x+
x+
x+
2
2
2
2
1
5
3 
x 5 2x + 3
x 5
=  x + ln( x + )  + C = + ln(
) + C = + ( ln(2x + 3) − ln 2 ) + C =
2
2
2 
2 4
2
2 4
x 5
= + ln(2x + 3) + C
2 4
47)
e2 x
1 2e 2 x
1
dx
=
dx = ln(e 2 x + 1) + C
2x
∫ e2 x + 1
∫
2 e +1
2
48)
(e x + 2)
x
∫ e x + 2x dx = ln(e + 2x) + C
1
1
ex
1 1
49) ∫ 2 dx = − ∫ − 2 e x dx = − e x + C
x
x
3
1 1
50) ∫ (1 + t ) t dt = − ∫ −t (1 + t ) dt = −  1 +  + C
3
t
−1 2 −2
−2
−1 2
51)
∫
1+ x
1
dx = ∫
1+ x
x
x
(
u = 1+ x = 1+ x
u'=
1
)
1
2
dx = 2 ∫
1
2 x
(
1+ x
)
1
2
3
4
dx = (1 + x ) 2 + C
3
2
1 − 12
1
x =
2
2 x
− x2
2
1
1 2
−2xe − x dx = − e − x + C
∫
2
2
52)
∫ xe
53)
∫ x (e
54)
∫ a e dx = ∫ ( ae )
55)
∫ sen5x dx = 5 ∫ 5sen5x dx = − 5 cos 5x + C
x2
dx = −
+ 2) dx = ∫ ( xe x + 2x) dx =
2
x x
1
2
1
1 2
2xe x dx + ∫ 2x dx = e x + x 2 + C
∫
2
2
( ae ) + C = a x e x + C = a x e x + C
ln ( ae )
ln e + ln a
1 + ln a
x
x
dx =
1
56)
∫ x sen ( 3x ) dx = 12 ∫ 12x sen ( 3x ) dx =
57)
∫ sen(2x + 1) dx = 2 ∫ 2sen(2x + 1) dx = − 2 cos(2x + 1) + C
3
1
4
3
4
1
−
( )
1
cos 3x 4 + C
12
1
58)
∫
sen x
1
dx = 2 ∫
sen x dx = − 2 cos x + C
x
2 x
u= x=x
u'=
1
2
1 − 12
1
x =
2
2 x
1
1
59)
∫ cos ( 8x ) dx = 8 ∫ 8 cos ( 8x ) dx = 8 sen ( 8x ) + C
60)
∫ cos(2x + 4) dx = 2 ∫ 2 cos(2x + 4) dx = 2 sen(2x + 4) + C
1
1
61)
∫
cos x
1
cos xdx = 2sen x + C
dx = 2 ∫
x
2 x
u= x=x
u'=
62)
1
2
1 − 12
1
x =
2
2 x
1
∫ cos(3x − 1) dx = 3 ∫ 3 cos(3x − 1) dx =
1
sen(3x − 1) + C
3
63)
∫ tg (5x
2
(
)
1
1
1
10x tg (5x 2 ) dx =
− ln cos(5x 2 ) + C = ln cos −1 (5x 2 ) + C =
∫
10
10
10
1
1
1
= ln
+ C = ln sec(5x 2 ) + C
2
10 cos(5x )
10
) x dx =
1
1
64)
∫ cot g (5x + 2) dx = 5 ∫ 5 cot g (5x + 2) dx = 5 ln sen(5x + 2) + C
65)
∫ cot g (5x) dx = 5 ∫ 5 cot g (5x) dx =
1
1
ln sen(5x) + C
5
senx + cos x
senx cos x
dx = ∫
+
dx = ∫ ( tgx + 1 ) dx = x + ln sec x + C
cos x
cos x cos x
66)
∫
67)
∫ sec x.senx = ∫
68)
∫ sec ( 2x ) dx
dx
dx
1
senx
cos x
=∫
cos x
dx = ∫ cot gx dx = ln senx + C
senx
1
1
2 sec ( 2x ) dx = ln sec ( 2x ) + tg ( 2x ) + C
∫
2
2
=
69)
∫
sec x
1
dx = 2 ∫
sec x dx = 2 ln sec x + tg x + C
x
2 x
u= x=x
u'=
1
2
1 − 12
1
x =
2
2 x
1
1
3 cos sec(3x) dx = ln cos sec 3x − cot g3x + C
∫
3
3
70)
∫ cos sec(3x) dx
=
71)
∫ sec ( 4x ) dx
1
1
4 sec2 ( 4x ) dx = tg ( 4x ) + C
∫
4
4
2
=
72)
tg 2 ( x )
1
2
2
1
sen 2 ( x )
1
2
2
2
∫ sen ( x ) dx = ∫ sen ( x ) tg ( x ) dx = ∫ sen ( x ) cos ( x ) dx = ∫ cos ( x ) dx =
= ∫ sec ( x ) dx = tg ( x ) + C
2
2
73)
∫ sec ( 2ax ) dx
74)
∫ cos ( 3x )
2
dx
2
=
=
1
1
2a sec 2 ( 2ax ) dx =
tg ( 2ax ) + C
∫
2a
2a
1
1
3 sec2 ( 3x ) dx = tg ( 3x ) + C
∫
3
3
75)
( 1 − cos x )
dx
1 − cos x
1 − cos x
dx = ∫
dx =
2
x
sen 2 x
∫ 1 + cos x = ∫ (1 + cos x )(1 − cos x ) dx = ∫ 1 − cos
(
)
1
cos x
−
dx = ∫ cos sec 2 ( x ) − cot g ( x ) cos sec ( x ) dx =
2
sen x sen 2 x
= − cot g ( x ) + cos sec ( x ) + C
=∫
76)
dx
1
1
∫ sen ( 5x ) = ∫ cos sec ( 5x ) dx = 5 ∫ 5 cos sec ( 5x ) dx = − 5 cot g ( 5x ) + C
77)
∫ sec(2x).tg ( 2x ) dx
2
2
2
=
1
1
2 sec(2x).tg ( 2x ) dx = sec ( 2x ) + C
∫
2
2
78)
(
)
2
2
2
∫ ( tg ( 2x ) + sec ( 2x ) ) dx = ∫ tg ( 2x ) + 2tg ( 2x ) sec ( 2x ) + sec ( 2x ) dx =
(
)
= ∫ −1 + sec2 ( 2x ) + 2tg ( 2x ) sec ( 2x ) + sec2 ( 2x ) dx =

 2

sen ( 2x )
sen ( 2x ) 
1
2

 dx =
= ∫  sec ( 2x ) − 1 + 2
 dx = ∫  sec ( 2x ) − 1 + 2
2
cos
2x
cos
2x

(
)
(
)
cos ( 2x ) 



(
)
= ∫ sec2 ( 2x ) − 1 + 2sen ( 2x ) cos −2 ( 2x ) dx = ∫ sec2 ( 2x ) dx − ∫ 1dx + ∫ 2sen ( 2x ) cos −2 ( 2 x ) dx =
Cálculos auxiliares
(cos−1 ( 2x )) = −1cos−2 ( 2x ) (cos ( 2x ))' = −1cos−2 ( 2x ) ( −2sen ( 2x )) =
'
= cos −2 ( 2x ) ( 2sen ( 2x ) ) = 2sen ( 2x ) cos −2 ( 2x )
logo,
∫ sec
2 2x dx − 1dx + 2sen 2x cos −2 2x dx =tg 2x − x + cos −1 2x + C =
( )
( )
( )
( )
( )
∫
∫
= tg ( 2x ) − x + sec ( 2x ) + C
79)
∫ (tg ( 2x ) − 1)
2
dx = ∫ (tg 2 ( 2x ) − 2tg ( 2x ) + 1) dx = ∫ (sec 2 ( 2x ) − 1 − 2tg ( 2x ) + 1) dx =
=
1
1
2 sec2 ( 2x ) dx − ∫ 2tg ( 2x ) dx = tg ( 2x ) + ln cos ( 2x ) + C
∫
2
2
sen ( 4x )
2sen ( 2x ) cos ( 2x )
80)
∫ cos ( 2x ) dx = ∫
81)
∫ cos
82)
∫ cos sec(2x) cot g ( 2x ) dx
83)
∫ sen x cos x dx = ∫ cos x sen x dx
cos ( 2x )
dx = ∫ 2sen ( 2x ) dx = − cos ( 2x ) + C
senx
senx 1
dx = ∫
dx = ∫ tgx sec x dx = sec x + C
2
x
cos x cos x
2
=
1
1
2 cos sec(2x) cot g ( 2x ) dx = − cos sec ( 2x ) + C
∫
2
2
2
=
1
sen 3 x + C
3
84)
∫
(1 + cos x )
1
1 + cos x
dx = ∫
dx = ∫
dx =
1 − cos x
(1 − cos x )(1 + cos x )
1 − cos 2 x
=∫
1 + cos x
1
cos x
dx = ∫
dx + ∫
dx = ∫ cos sec2 xdx + ∫ cos xsen−2 xdx =
2
2
2
sen x
sen x
sen x
= ∫ cos sec 2 xdx + ∫ cos xsen −2 xdx = − cot gx −
1
+ C = − cot gx − cos sec x + C
cos x
85)
∫
1
1 − senx
1 − senx
1 − senx
dx = ∫
dx = ∫
dx = ∫
dx =
1 + senx
( 1 + senx )( 1 − senx )
1 − sen2 x
cos2 x
 1
senx 
1
senx
= ∫
−
dx = ∫
dx − ∫
dx =

2
2
2
2
cos x
cos x
 cos x cos x 
1 senx
= ∫ sec2 xdx − ∫
dx = ∫ sec2 xdx − ∫ sec x tgxdx = tgx − sec x + C
cos x cos x
86)
∫
1 − cos x .senx dx = ∫ senx ( 1 − cos x ) 2 dx =
1
3
2
(1 − cos x) 2 + C
3
u = 1 − cos x
u ' = senx
87)
( )
∫ sen ( x ) dx = ∫ cot g ( x ) cos sec ( x ) dx =
cos x
3
2
1
− cos sec2 ( x ) + C
2
88)
∫e
3 cos( 2 x )
sen ( 2x ) dx =
u = 3 cos ( 2x )
1
1 3 cos 2 x
3 cos 2 x
6 sen ( 2x ) e ( ) dx = − e ( ) + C
∫
6
6
u ' = −6 sen ( 2x )
89)
∫e
senx
cos x dx = ∫ cos x e senx dx = e senx + C
u = senx
u ' = cos x
90)
∫e
tgx
sec 2 x dx = ∫ sec 2 x etgx dx = etgx + C
u = tgx
u ' = sec 2 x
91)
∫e
cos( 2 x )
sen ( 2x ) dx = −
u = cos ( 2x )
1
1
−2sen ( 2x ) ecos( 2 x ) dx = − ecos( 2 x ) + C
∫
2
2
u ' = −2sen ( 2x )
92)
senx
∫ 1 − cos x dx = ln 1 − cos x + C
u = 1 − cos x
u ' = senx
93)
∫
sec ( 2x ) tg ( 2x )
3 sec ( 2x ) − a
u = 3 sec ( 2x ) − a
dx =
u ' = 6 sec ( 2x ) tg ( 2x )
1 6 sec ( 2x ) tg ( 2x )
1
dx = ln 3 sec 2x − a + C
∫
6
3 sec ( 2x ) − a
6
94)
sec ( x ) tg ( x )
∫ a + b sec ( x )
dx =
u = a + b sec ( x )
1 b sec ( x ) tg ( x )
1
dx = ln a + b sec ( x ) + C
∫
b a + b sec ( x )
b
u ' = b sec ( x ) tg ( x )
95)
sec2 x
∫ 1 + tgx dx = ln 1 + tgx + C
u = 1 + tgx
u ' = sec2 x
96)
∫
cos ( ax )
b + sen ( ax )
dx =
1
2
a cos ( ax ) b + sen ( ax ) dx =
b + senax + C
∫
a
a
u = b + sen ( ax )
u ' = a cos ( ax )
97)
sec2 x
∫ 1 + tg 2 x dx = arctg (tgx) + C
98)
(1 + x )3
1
(1 + x )4
3
dx
=
2
(
1
+
x
)
dx
=
+C
∫ x
∫2 x
2
u= x=x
u'=
1
2
1 − 12
1
x =
2
2 x
99)
∫ (t
2
t −2
1
dt = ∫ 2 ( t − 2 ) (t 2 − 4t + 3) −3 dt =
3
− 4t + 3)
2
1
−1
= ∫ ( 4t − 4 ) (t 2 − 4t + 3)−3 dt = 2
+C
2
4 (t − 4t + 3) 2
u = t 2 − 4t + 3
u ' = 2t − 4
100)
xdx
3
x2 3
=
arctg
+C
∫ x4 + 3 6
3
101)
∫ 9x
dx
1  3x − 4 
=
ln 
+C
24  3x + 4 
− 16
2