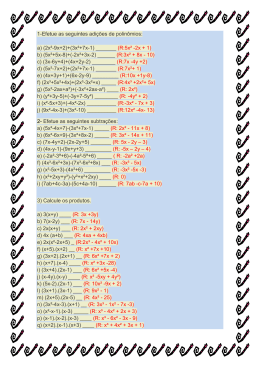
Questão
02
UNICAMP 2ª Fase
Curso e
Colégio
2º dia 12/01/15
Seja 𝑎 um número real positivo e considere as funções afins 𝑓(𝑥)=𝑎𝑥+3𝑎 e 𝑔(𝑥)=9−2𝑥, definidas para todo número
real 𝑥.
a) Encontre o número de soluções inteiras da inequação 𝑓(𝑥)𝑔(𝑥)>0.
b) Encontre o valor de 𝑎 tal que 𝑓(𝑔(𝑥))= 𝑔(𝑓(𝑥)) para todo número real 𝑥.
Curso e
Colégio
RESPOSTA
a)
b)
a>0
f(g(x)) = f(9 – 2x)
a (x+3) (9-2x)>0
f(g(x)) = a (9 – 2x) + 3ª (I)
x + 3 = 0 → x = -3
g(f(x)) = g(ax + 3a)
9 - 2x = 0 → x = 9/2
g(f(x)) = 9 – 2(ax + 3ª) (II)
Igualando (I) e (II)
9ª – 2ax + 3a = 9 – 2ax – 6a
S={xϵR / -3<x<9/2}
18a = 9
a = 1/2
A inequação a (x+3) (9-2x) > 0 possui 7 soluções
inteiras, ou seja, { -2, -1, 0, 1, 2, 3, 4}