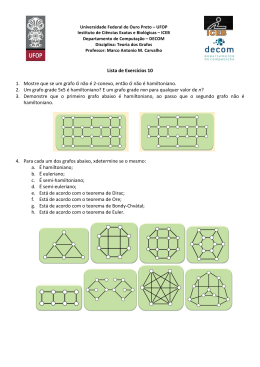
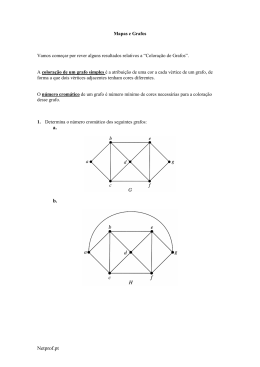
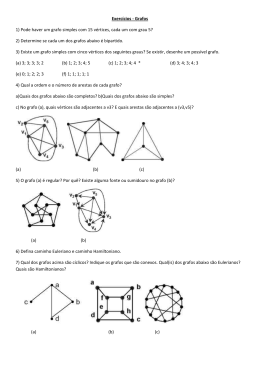
Teoria dos Grafos 2ª Lista - Período 2005.1 1. Considere a figura abaixo que mostra a planta baixa de uma casa. É possível identificar portas que dividem os diversos cômodos da casa e portas que dão acesso à parte externa da casa. Utilize a teoria dos grafos para determinar se é possível começar do lado de fora da casa, entrar na casa e visitar cada cômodo uma única vez (sem deixar a casa) e, finalmente sair da casa. Se sim, mostre uma rota possível. Caso não seja possível, justifique a sua conclusão. 2. Todo grafo completo possui um ciclo Euleriano? Justifique a sua resposta. 3. Todo grafo Euleriano é Hamiltoniano. Se esta afirmação é verdadeira, justifique a sua resposta. Se for falsa, apresente um contra-exemplo. 4. Considere o grafo definido pela matriz de adjacências abaixo. a. Mostre sua representação gráfica. b. Ele é um grafo Euleriano? Se sim, encontre um ciclo Euleriano. Caso contrário, indique como transformá-lo em um grafo Euleriano. A B C D E F G A 0 1 1 0 1 0 1 B 1 0 1 1 0 1 0 C 1 1 0 1 0 1 0 D 0 1 1 0 1 0 1 E 1 0 0 1 0 1 1 F 0 1 1 0 1 0 1 G 1 0 0 1 1 1 0 5. Qual a diferença entre grafo completo e grafo conexo? Existe relação entre esses dois tipos de grafos? 6. Todo grafo Euleriano simples com um número par de vértices tem um número par de arestas. 7. Um grafo é bipartido se e somente se ele não contém ciclos de comprimento ímpar. 8. Para cada uma das seqüências abaixo, determinar se existe uma grafo cuja seqüência de graus é a especificada. Se existir, mostre sua representação gráfica e sua representação por matriz de adjacências. a. 2, 3, 4, 4, 4 b. 1, 2, 3, 4, 5, 5
Baixar