Universidade Tecnológica Federal do Paraná
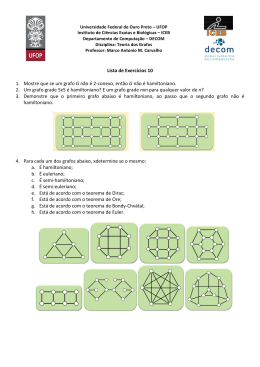
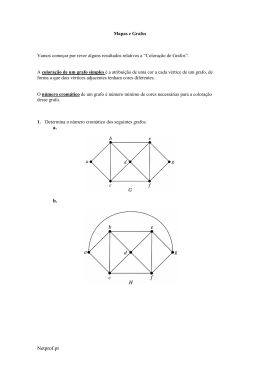
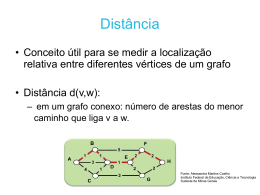
Professor Murilo V. G. da Silva
Notas de aula – Projeto e Análise de Algoritmos
MATERIAL OPCIONAL 4 (AVANÇADO)
1
Probabilidade a serviço da computação: Como mostrar a existência
de uma estrutura combinatória sem saber nada sobre ela
No nosso curso vimos vários algoritmos probabilı́sticos e algumas provas de existência que puderam ser
transformadas em algoritmos probabilı́sticos. Vamos mostar agora uma prova de existência que, embora não
nos forneça algoritmos probabilı́sticos como vimos com o caso do Corte Mı́nimo ou do MaxSAT, vale a pena se
estudada por tratar-se de um resultado importante em teoria dos grafos. A primeira pessoa a provar tal teorema
foi o famoso matemático Paul Erdös.
Provaremos que existem grafos com cintura1 e número cromático arbitrariamente altos. Formalmente o teorema é enunciado assim:
Teorema: ∀k ≥ 2, existe um grafo G tal que χ(G) > k e γ(G) > k
Prova: A ideia principal por trás desta prova é construir um espaço amostral finito e discreto, onde cada
elemento é um grafo com n vértices. O ponto chave é definir uma distribuição de probabilidades neste espaço
de maneira que um grafo com as propriedades desejadas tenha probabilidade maior do que zero para algum n
“grande”. Com isso concluı́mos que tal grafo existe, mesmo que não saibamos nada sobre ele.
ˆ Seja V = {v1 , v2 , ..., vn } e seja 0 ≤ p ≤ 1 um número fixo, mas que será escolhido mais adiante.
ˆ Seja Ω = G(n, p) = {“todos os grafos sobre V com cada aresta aparecendo com probabilidade p”}
7
Exemplo 1: No espaço de probabilidade Ω = G(7, p) os elementos são os 2(2) grafos com os 7 vértices
7
v1 , ..., v7 . O grafo K7 ∈ Ω tem a probabilidade P r(K7 ) = p(2) associada a ele (que é probabilidade de que
a a primeira aresta apareça e a segunda aresta e a terceira aresta... Já no caso do grafo de 7 vértices sem
7
nenhuma aresta tem probabilidade é (1 − p)(2) .
n
Exemplo 2: Kn ∈ Ω e P r(Kn ) = p( 2 )
n
Exemplo 3: H ∈ Ω e P r(H) = pm (1 − p)( 2 )−m , onde m = |E(H)|
Exemplo 4: Digamos que fixamos o valor p = 1, então no nosso espaço amostral G(n, 1) consiste de todos os
grafos com n vértices. Neste caso temos que P r(Kn ) = 1 e que todos os demais grafos tem probabilidade
zero. Em geral, se fixarmos p próximo de 1, grafos mais densos terão probabilidade maior de aparecer e se
fixarmos p próximo de zero, grafos mais esparsos. O ponto chave é escolher n e p de maneira que o grafo
desejado G tenha probabilidade maior do que zero, mesmo que não saibamos nada sobre G!
Em nossa prova temos que provar que o número cromático é “alto” (lembre que queremos que para qualquer
k dado, a χ(G) ≥ k) e que a cintura do grafo também é grande (≥ k). Vamos dividir nossa prova em três partes.
Na primeira, mostraremos que α(G) é pequeno, pois isso implica χ(G) é grande (pense a respeito). Na segunda
parte vamos mostrar que o grafo tem “poucos” ciclos pequenos, o que nos será útil para provar que existem
grafos sem nenhum ciclo pequeno (≤ k). Na terceira parte juntamos os resultados da primeira e segunda parte
para terminar a prova do teorema.
Primeira parte da prova: α(G) é pequeno
ˆ Fato 1: χ(G) ≥
α(G)
n
para qualquer grafo G.
Seja R ⊆ V tal que |R| = r e seja Ir o evento que α(G[R]) = r
1A
cintura de um grafo é o tamanho de seu menor ciclo
1
r
ˆ Fato 2: P r(Ir ) = (1 − p)(2)
r
Portanto P r(α(G) ≥ r) ≤ nr (1 − p)(2) . A partir daı́:
r
r
r−1
ˆ P r(α(G) ≥ r) ≤ nr (1 − p)(2) ≤ nr (1 − p)(2) = (n(1 − p) 2 )r ≤ (ne−p(r−1)/2 )r
Agora vamos olhar para o k (do enunciado do teorema) para fixar p do nosso G(n, p).
k
ˆ Seja p = n− k+1 .
1
Antes de seguir em frente observe o seguinte: Como n k+1 cresce mais rápido que ln n, temos que para um
1
n
n suficientemente grande n k+1 ≥ 6k ln n. Disto temos que p ≥ 6k lnnn . Em particular, fazendo r = d 2k
e, temos
pr
≥
3
ln
n
o seguinte fato que será útil adiante:
n.
1
2
n
e) <
Afirmação 1: Para n ≥ n1 , P r(α(G) ≥ d 2k
Vimos anteriormente que P r(α(G) ≥ r) ≤ (ne−p(r−1)/2 )r . Para mostrar a Afirmação 1, vamos nos focar
apenas em ne−p(r−1)/2 (e ignorar o expoente) e mostrar que isso pode ser tão pequeno quanto se queira, ou
seja, tende a zero. Vamos a contarada:
ne−p(r−1)/2 = ne−
pr
2
p
1
3
1
1
e 2 ≤ ne− 2 ln n e 2 = n− 2 e 2 =
e 21
n
1
2
Como ( ne ) converge para zero quando n vai para o infinito, provamos a Afirmação 1. Isso finaliza a primeira
parte da prova, onde querı́amos mostrar que α é pequeno.
Segunda parte da prova: O grafo tem poucos ciclos pequenos
Vamos agora provar que existem poucos ciclos pequenos (ciclos com ≤ k vértices). Lembramos que idealmente não queremos nenhum ciclo ≤ k, mas daremos conta disto no fim da demonstração.
Seja 3 ≤ i ≤ k e seja I ⊆ V ; |I| = i. Temos que:
ˆ O número possı́veis de ciclos em I é
(i−1)!
2 ;
ˆ O número total de i-ciclos possı́veis é
n (i−1)!
i
2
e a probabilidade de cada ciclo é pi ;
Seja X a v.a. que conta o número de ciclos ≤ k e seja XC um v.a. indicadora de um dado ciclo C.
ˆ Com isso E[XC ] = pi , onde i é o tamanho do ciclo;
Pela linearidade da esperança temos:
E[X] =
k X
n (i − 1)!
i=3
i
2
k
pi ≤
1X i i
1
n p ≤ (k − 2)nk pk
2 i=3
2
Usando a desigualdade de Markov temos:
P r(X ≥
1
n
E[X]
(np)k
)≤
≤ (k − 2)
= (k − 2)n− k+1
2
n/2
n
1
Como (k − 2)n− k+1 tende a zero quando n → ∞, então para n ≥ n2 , P r(X ≥
n
2)
≤ 21 .
Terceira parte da prova: Colocando tudo junto
Estamos quase lá. Para n ≥ max(n1 , n2 ), existe um grafo H com n vértices tal que α(H) <
menos do que n2 ciclos de tamanho ≤ k. Para fechar a prova faça o seguinte:
2
n
2k
e H contém
ˆ Remova um vértice de cada ciclo de H. Seja G o grafo resultante;
ˆ Obviamene γ(G) > k;
ˆ Como |V (G)| >
n
2
e G satisfaz α(G) ≤ α(H) <
χ(G) ≥
n
2k
temos:
n
n
n/2
≥
>
=k
α(G)
2α(G)
n/k
Assim a prova do teorema está finalizada. 2
3