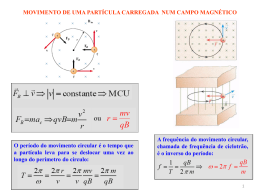
Quando um ímã é dividido ao meio  resulta em dois novos ímãs, cada um com um
pólo norte e um pólo sul porque não é possível separar o pólo norte do pólo sul
1
SUMÁRIO DO ESTUDO SOBRE O MAGNETISMO
1. Introdução:
Anteriormente falamos sobre a história do
magnetismo e dos propriedades dos imanes
2. Linhas do Campo magnético no imane
3. Definição de campo magnético e força magnética
4. Força magnética sobre: i) uma partícula carregada com velocidade
num campo magnético, ii) um condutor com corrente eléctrica num
campo magnético.
5. Fontes do campo magnético: campo magnético criado por uma
corrente num condutor (lei de Biot-Savart, lei Ampère), magnetismo na
matéria.
6. Campo eléctrico devido à um
campo magnético variável (lei de
Faraday).
2
2. Linhas do Campo magnético no imane
O campo magnético é um campo vectorial, similar ao campo eléctrico
O campo magnético B é tangente, em cada ponto, às linhas de campo magnético
Uma pequena bússola pode ser utilizada para traçar as
linhas do campo magnético de uma barra imanada.
3
PADRÕES DE CAMPO MAGNÉTICO AO REDOR DE UMA BARRA IMANADA EVIDENCIADOS POR
LIMALHAS DE FERRO
Íman de barra
4
3. Definição de campo magnético e força magnética
FORÇA MAGNÉTICA
A existência
 de campo magnético em algum ponto do espaço pode ser determinada medindo-se
a força FB que actua sobre uma partícula de teste apropriada colocada nesse ponto.
A partícula de teste será uma partícula electricamente carregada, (como um protão) e terá uma
velocidade.
Verificou-se que
- A força magnética é proporcional à carga q da partícula, bem como à velocidade da partícula.
- O módulo e a direcção da força magnética sobre a partícula
dependem da direcção relativa entre o vector velocidade da partícula
e o vector campo magnético

FB
- Quando uma partícula carregada se desloca paralelamente ao vector
campo magnético, a força magnética sobre a carga é nula.
- Quando o vector velocidade faz um ângulo  com o campo
magnético,
a força magnética age numa direcção perpendicular

a v e a B isto
 é, a força magnética é perpendicular ao plano
formado por v e B .  Figura (a)
5
- A força magnética sobre uma carga negativa tem direcção oposta à força sobre uma carga
positiva que se desloca na mesma direcção.  Figura (b)
- Se o vector velocidade fizer um ângulo  com o campo magnético, o valor da força
magnética será proporcional a sin .
Esses resultados mostram que a força magnética sobre uma
partícula é mais complicada do que a força eléctrica:


Fe  qE
Podemos resumir de uma maneira compacta escrevendo a
força magnética na forma

 
FB  qv  B
Módulo da força magnética
FB  q vB sin 
Módulo do campo magnético
FB
B
q v sin

Unidade do campo magnético B no SI é o tesla: 1 T = 1 N s/C m
6
REGRA DA MÃO DIREITA PARA DETERMINAR A DIRECÇÃO DA FORÇA MAGNÉTICA

 
FB  qv  B
FB  q vB sin 90  q vB

FB  q vB sin 0  0
7
4. Força magnética sobre: i) uma partícula carregada com velocidade num
campo magnético, ii) um condutor com corrente eléctrica num campo
magnético.
(a) A força eléctrica que actua sobre
uma carga positiva é paralela ao campo
eléctrico (E) e faz com que a trajectória
dessa carga seja uma curva no plano
horizontal.
MOVIMENTO DE UMA PARTÍCULA CARREGADA
NUM CAMPO MAGNÉTICO
(b) A força magnética é perpendicular tanto
ao vector velocidade (v) como ao campo
magnético (B), fazendo com que a trajectória
da partícula seja uma curva no plano
vertical.
8
MOVIMENTO DE UMA PARTÍCULA CARREGADA NUM CAMPO MAGNÉTICO
 entrando na página
 saindo da página
9
Duas cargas de mesma massa mas de diferentes cargas positivas
10
MOVIMENTO DE UMA PARTÍCULA CARREGADA NUM CAMPO MAGNÉTICO
O período do movimento circular é o tempo que
a partícula leva para se deslocar uma vez ao
longo do perímetro do círculo:
A frequência do movimento circular,
chamada de frequência de ciclotrão,
é o inverso do período:
11
Se uma partícula carregada se deslocar no campo magnético uniforme com uma
velocidade que faz um ângulo arbitrário  em relação ao campo magnético, a sua
trajectória é uma hélice

 
FB  qv  B
FB
FB  q vB sin 
B

+q
v
Não existe componente de força na direcção

paralela a B  a componente da velocidade
nesta direcção permanece constante.
v  v y  vz
2
A força magnética

B
perpendicular a
2
sobre
a
partícula
é
Resulta que a trajectória da partícula é helicoidal
12
Exemplo
Quando uma partícula carregada se move em espiral num campo magnético não uniforme, que é
forte em ambas as extremidades e fraco no meio, ela fica aprisionada e se desloca para frente e
para trás numa trajectória espiral em torno das linhas de campo.
Desta maneira, electrões e protões ficam aprisionados pelo campo magnético terrestre não
uniforme, formando os cinturões de radiação de Van Allen
13
Partículas de alta energia aprisionadas no campo
magnético da Terra (descobertos por James Van
Allen em 1958, a partir das primeiras observações
da Terra feitas por satélite, os cinturões marcam o
início da investigação moderna em física
espacial).
Aurora Boreal. Luminescência visível
resultante da excitação de átomos e
moléculas
da
atmosfera,
quando
bombardeados por partículas carregadas
expelidas do Sol e deflectidas pelo campo
geomagnético.
14
APLICAÇÕES DO MOVIMENTO DE PARTÍCULAS CARREGADAS NUM CAMPO
MAGNÉTICO
FILTRO DE VELOCIDADES
Uma partícula carregada positivamente entra numa região do
espaço entre as placas de um condensador onde existem um
campo eléctrico e um campo magnético perpendicular (como o
produzido por um imane).
A força total que actua sobre a partícula é :

  
F  qE  qv  B
 Força de Lorentz
As forças eléctrica e magnética são invertidas. As duas forças se equilibram (e,
portanto, a partícula não sofre desvio) e desloca-se numa linha recta horizontal
qE  qvB
E
 v
B
15
Somente as partículas que têm essa velocidade
v
E
B
não são desviadas.
Cargas com velocidades maiores são desviadas para cima e com velocidades menores,
desviadas para baixo.
16
ESPECTRÔMETRO DE MASSA
Com o espectrómetro de massa determina-se massas atómicas com grande precisão
De acordo com o esquema da figura, uma fonte produz
íões com carga eléctrica q=Ze (positiva) e massa M de
velocidades variadas.
Os iões entram num filtro de velocidade. Atravessam
o filtro apenas os iões para os quais a força
magnética e a força eléctrica se cancelam
mutuamente, isto é, iões com velocidade
v
E
B
Saindo do filtro, os iões entram numa região onde existe apenas o campo magnético uniforme, de
forma que percorrem trajectórias circulares de raio R sob o efeito da força magnética, que faz o
papel de força centrípeta. Assim:
mv 2
 qvB 0
r

m rB 0

q v
ou
m rB 0 B

q
E
17