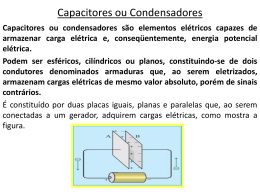
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Capacitores e Dielétricos
Um capacitor é um sistema elétrico formado por dois condutores
separados por um material isolante, ou pelo vácuo.
Imaginemos uma configuração como a de um capacitor em que os
dois condutores estejam inicialmente descarregados (com carga
líquida nula). O processo chamado de carregamento de um capacitor
consiste em transferir elétrons de um dos condutores para o outro de
maneira que, no fim do processo, um dos condutores esteja com
carga líquida positiva +Q e o outro condutor esteja com carga
líquida negativa −Q. Note que a carga líquida total do sistema
formado pelos dois condutores continua nula.
Após o carregamento de um capacitor, dizemos que ele armazena ou
possui carga Q.
Note que entre os dois condutores de um capacitor carregado existe
um campo elétrico ‫ܧ‬ሬԦ que aponta do condutor com carga +Q para o
condutor com carga −Q. Consequentemente, o condutor com carga
+Q está a um potencial maior que o condutor com carga −Q.
1
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Nos diagramas de circuitos elétricos, representa-se um capacitor
pelo símbolo abaixo:
.
Uma maneira de carregar um capacitor é ligar fios metálicos aos
condutores e conectá-los aos terminais opostos de uma bateria.
Espera-se até que as cargas +Q e −Q se estabeleçam nos dois
condutores e depois desconectam-se os fios da bateria. Como as
cargas não podem passar de um condutor para outro, a carga
armazenada no capacitor permanece constante. A voltagem Vab entre
os condutores (Va − Vb) permanece constante e é igual à voltagem da
bateria.
Capacitor de placas planas e paralelas
Consideremos um capacitor cujos condutores sejam placas metálicas
planas e paralelas carregadas com cargas +Q e −Q. Vamos supor que
as placas têm área A e estejam separadas por uma distância d.
2
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Se a distância d for muito menor que a área das placas, podemos
tratá-las, aproximadamente e longe das bordas, como se fossem
planos infinitos. Neste caso, como visto em aulas anteriores, o
campo elétrico entre as placas é uniforme, aponta da placa carregada
positivamente para a carregada negativamente e seu módulo vale
ߪ
(1)
‫ = ܧ‬ห‫ܧ‬ሬԦ ห = ,
ߝ଴
onde σ é a densidade superficial de carga nas placas do capacitor,
ܳ
.
‫ܣ‬
A diferença de potencial entre as duas placas é
ߪ=
ି
ሬԦ = ‫݀ܧ‬,
ܸ = ܸା − ܸି = න ‫ܧ‬ሬԦ ∙ ݀ℓ
ା
(2)
(3)
o que implica que, substituindo (1) em (3):
ܸ=
ߪ݀ ܳ݀
=
.
ߝ଴ ߝ଴ ‫ܣ‬
(4)
A diferença de potencial entre as placas é proporcional à carga Q
armazenada.
Este resultado vale para qualquer capacitor: a diferença de potencial
V entre dois condutores, de qualquer forma, carregados com carga Q
é proporcional a Q.
Invertendo a equação (4), podemos escrever Q em função de V:
3
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
ܳ=
ߝ଴ ‫ܣ‬
ܸ.
݀
(5)
‫≡ܥ‬
ߝ଴ ‫ܣ‬
݀
(6)
Define-se
como a capacitância do capacitor (como vimos, esta relação vale
para qualquer capacitor). Portanto, a relação entre a carga
armazenada num capacitor e a diferença de potencial entre os
condutores é
ܳ = ‫ܸܥ‬.
(7)
A unidade de capacitância é o farad (F), em homenagem a Michael
Faraday (veja a aula 3).
஼
1 farad = 1 F = 1 = 1
௏
ୡ୭୳୪୭୫ୠ
୴୭୪୲
.
Quanto maior for a capacitância de um capacitor, maior a carga Q
armazenada no capacitor para uma mesma diferença de potencial.
A equação (6) nos permite escrever as unidades da constante ε0 em
termos do farad:
ሾߝ଴ ሿ = ሾ‫ ܥ‬ሿ
ou
ሾ݀ ሿ F
= ,
ሾ‫ܣ‬ሿ m
ε0 = 8,85 × 10−12 F/m.
4
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Capacitor esférico
Um capacitor esférico é formado por uma esfera condutora interna
de raio ra e uma casca esférica condutora concêntrica de raio rb. As
duas estão separadas pelo vácuo. A esfera interna tem carga +Q
distribuída por sua superfície externa e a casca esférica externa tem
carga −Q distribuída por sua superfície interna (figura abaixo).
Para calcular a capacitância desse capacitor, vamos usar a relação
(7), que é válida para qualquer capacitor:
‫=ܥ‬
ܳ
.
ܸ
(8)
Para determinar V, precisamos determinar o campo elétrico ‫ܧ‬ሬԦ entre a
esfera e a casca esférica.
Tomemos uma superfície gaussiana de raio r entre a esfera e a casca
esférica. O fluxo elétrico por essa superfície vale Q/ε0:
5
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Φா = ර ‫ܧ‬ሬԦ ∙ ݀‫ܣ‬Ԧ =
ܳ
.
ߝ଴
Por simetria, ‫ܧ‬ሬԦ é constante em módulo ao longo dessa superfície
gaussiana. Ele também aponta na direção radial, que coincide com a
direção de ݀‫ܣ‬Ԧ. Logo
Φா = ‫ܧ = ܣܧ‬4ߨ‫ ݎ‬ଶ =
ܳ
.
ߝ଴
Então,
‫=ܧ‬
1 ܳ
.
4ߨߝ଴ ‫ ݎ‬ଶ
O campo elétrico entre a esfera e a casca esférica é igual ao de uma
carga puntiforme +Q colocada no centro delas. Como o campo
elétrico é o mesmo de uma carga puntiforme no centro, o potencial
elétrico também o será:
ܸ=
1 ܳ
.
4ߨߝ଴ ‫ݎ‬
Portanto, a diferença de potencial entre a esfera de raio ra e a casca
esférica de raio rb é
ܸ௔௕ = ܸ௔ − ܸ௕ =
=
ܳ
ܳ
ܳ
1 1
−
=
൬ − ൰
4ߨߝ଴ ‫ݎ‬௔ 4ߨߝ଴ ‫ݎ‬௕ 4ߨߝ଴ ‫ݎ‬௔ ‫ݎ‬௕
ܳ ‫ݎ‬௕ − ‫ݎ‬௔
.
4ߨߝ଴ ‫ݎ‬௔ ‫ݎ‬௕
A capacitância do capacitor esférico é então
‫=ܥ‬
ܳ
‫ݎ‬௔ ‫ݎ‬௕
= 4ߨߝ଴
.
ܸ௔௕
‫ݎ‬௕ − ‫ݎ‬௔
(9)
6
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Um caso particular da equação (9) ocorre para o caso em que a casca
esférica de raio rb está muito longe da esfera de raio ra. Se a
distância entre elas for tão grande que se possa aproximar rb → ∞, a
capacitância do sistema torna-se
‫ݎ‬௔ ‫ݎ‬௕
‫ = ܥ‬4ߨߝ଴
= 4ߨߝ଴ ‫ݎ‬௔ ,
‫ݎ‬௕
(10)
ou seja, a capacitância depende apenas do raio da esfera interna.
Podemos então definir a capacitância de uma esfera condutora de
raio R como:
‫ = ܥ‬4ߨߝ଴ ܴ.
(11)
As linhas de força entre a esfera de raio R e a casca esférica de raio
“infinito” se estendem até o “infinito”.
Por exemplo, se pudermos tratar a Terra como uma esfera condutora
esférica, sua capacitância vale (o raio da Terra é R ≅ 6,37 × 103 km)
CTerra ≅ 7,1 × 10−4 F = 710 µF.
Este é um valor bastante grande. Tão grande que podemos supor, em
geral, que quando se escoa uma quantidade de carga ∆Q para a Terra
a alteração no seu potencial é desprezível (veja abaixo)
Δܸ =
Δܳ
.
‫ܥ‬
É por isso que a Terra é um bom “terra”.
7
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Capacitor cilíndrico
Um capacitor cilíndrico é formado por um cilindro condutor de raio
ra e densidade linear de carga λ1 circundado por uma casca cilíndrica
condutora coaxial de raio interno rb e densidade linear de carga −λ
(veja a figura abaixo).
Para calcular a diferença de potencial entre os cilindros, lembremos
que p potencial em um ponto externo a um cilindro carregado a uma
distância r do centro vale
ܸ=
‫ݎ‬଴
ߣ
ln ,
2ߨߝ଴ ‫ݎ‬
onde r0 é uma distância arbitrária onde V = 0. Podemos usar esta
expressão aqui porque a carga elétrica sobre a casca cilíndrica
externa não contribui para o potencial no interior do cabo coaxial.
1
Para relacionar a densidade linear de carga λ com a densidade superficial de carga σ, mais usual quando se
trata de superfícies, basta lembrar que a carga total em um comprimento L do cilindro é Q = λ L = σA =
2πraLσ. Isto nos dá: λ = 2πraσ.
8
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Vamos escolher r0 = rb, o raio da parte de dentro da casca cilíndrica
externa. Então, o potencial em ra será
ܸ௔௕ = ܸ (ܽ) − ܸ (ܾ) =
ߣ
‫ݎ‬௕
ߣ
‫ݎ‬௕
ln − 0 =
ln .
2ߨߝ଴ ‫ݎ‬௔
2ߨߝ଴ ‫ݎ‬௔
(12)
Essa diferença é positiva, pois V(a) > V(b).
Para calcular a capacitância, vamos usar a fórmula C = Q/Vab. A
carga Q é dada por Q = λL, de maneira que
‫=ܥ‬
2ߨߝ଴ ‫ܮ‬
‫ݎ‬௕ .
ln ቀ ቁ
‫ݎ‬௔
(13)
A capacitância por unidade de comprimento é, então
‫ܥ‬
2ߨߝ଴
=
.
‫ ܮ‬ln ቀ‫ݎ‬௕ ቁ
‫ݎ‬௔
(14)
Note que, assim como nos casos dos capacitores de placas planas
paralelas e esférico, a capacitância do capacitor cilíndrico depende
apenas das dimensões do capacitor.
Substituindo ε0 = 8,85 × 10−12 F/m = 8,85 pF/m em (14), obtemos
uma expressão útil para a capacitância por unidade de comprimento:
‫ ܥ‬55,6 pF/m
=
‫ݎ‬௕ .
‫ܮ‬
ln ቀ ቁ
‫ݎ‬௔
(15)
9
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Capacitores em série e em paralelo
A figura (a) abaixo mostra o diagrama de circuitos para um arranjo
de capacitores denominado de arranjo em série. Em um arranjo
desse tipo, dois ou mais capacitores são conectados um após o outro
(em série) por fios condutores. Os terminais do circuito estão ligados
aos polos de uma bateria, de maneira que a diferença de potencial
entre eles é V.
A placa superior do capacitor de capacitância C1 acumula carga +Q.
Portanto, a placa inferior desse capacitor possui carga −Q. Os
elétrons que se acumulam nessa placa vieram da placa superior do
segundo capacitor (com capacitância C2). Desta forma, a placa
superior desse segundo capacitor também tem carga +Q e a placa
inferior tem carga −Q.
Quando capacitores são conectados em série, cada um deles possui a
mesma carga.
10
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
A partir deste resultado, podemos escrever que as diferenças de
potencial entre os pontos a e c e c e b na figura são:
ܸ௔௖ = ܸଵ =
ܳ
‫ܥ‬ଵ
e
ܸ௖௕ = ܸଶ =
ܳ
.
‫ܥ‬ଶ
Isto implica que
ܸ௔௕ = ܸ = ܸଵ + ܸଶ = ܳ ൬
1
1
+ ൰.
‫ܥ‬ଵ ‫ܥ‬ଶ
Isto sugere que podemos substituir os dois capacitores em série no
circuito acima por um único capacitor equivalente com capacitância
‫ܥ‬ୣ୯ =
1
1
+ .
‫ܥ‬ଵ ‫ܥ‬ଶ
A figura (b) acima mostra o capacitor equivalente.
Generalizando, se tivermos N capacitores em série em um circuito
eles podem ser substituídos por um capacitor equivalente com
capacitância
‫ܥ‬ୣ୯ =
1
1
1
+ + ⋯+ .
‫ܥ‬ଵ ‫ܥ‬ଶ
‫ܥ‬ே
(16)
A figura abaixo mostra um arranjo de capacitores em um circuito
denominado de arranjo em paralelo.
11
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Note que os terminais dos capacitores estão ligados aos mesmos
polos da bateria, de maneira que as diferenças de potenciais entre
eles são todas iguais a V.
Vamos supor que a carga total presente no circuito vale Q e ela se
encontra distribuída pelos capacitores de maneira que o primeiro
possui carga Q1 e o segundo possui carga Q2:
Q = Q1 + Q2.
(17)
Temos, então
ܳ = ‫ܥ‬ଵ ܸ + ‫ܥ‬ଶ ܸ = (‫ܥ‬ଵ + ‫ܥ‬ଶ )ܸ.
Isto sugere que podemos substituir os dois capacitores em paralelo
no circuito acima por um único capacitor equivalente com
capacitância
‫ܥ‬ୣ୯ = ‫ܥ‬ଵ + ‫ܥ‬ଶ .
O capacitor equivalente está mostrado na figura (b) acima.
12
IBM1018 – Física Básica II – FFCLRP – USP – Prof. Antônio Roque – Aula 9
Generalizando, se tivermos N capacitores em paralelo em um
circuito eles podem ser substituídos por um capacitor equivalente
com capacitância
‫ܥ‬ୣ୯ = ‫ܥ‬ଵ + ‫ܥ‬ଶ ⋯ ‫ܥ‬ே .
(18)
13