Universidade Federal do ABC
Curso de Pós-Graduação em Ciência da Computação
Dissertação de Mestrado
Edilson José Rodrigues
Um Algoritmo para o Problema do
Isomorfismo de Grafos
Santo André
2014
Universidade Federal do ABC
Curso de Pós-Graduação em Ciência da Computação
Dissertação de Mestrado
Edilson José Rodrigues
Um Algoritmo para o Problema do
Isomorfismo de Grafos
Trabalho apresentado como requisito parcial para a obtenção do título de Mestre em
Ciência da Computação, sob orientação do
Professor Doutor Daniel Morgato Martin.
Santo André
2014
Resumo
Neste trabalho estudamos o Problema do Isomorﬁsmo de Grafos e a sua complexidade para resolvê-lo. Nossa principal contribuição é a proposta de um algoritmo
para o caso geral do Problema, baseado no particionamento do conjunto de vértices
e em emparelhamentos perfeitos de grafos bipartidos.
Estudamos também o algoritmo de Brendan McKay, que é o mais rápido algoritmo
para o Problema do Isomorﬁsmo de Grafos conhecido. Ao ﬁnal, implementamos o
algoritmo proposto nesta dissertação e o algoritmo de McKay.
Após a comparação dos dois algoritmos, veriﬁcamos que os resultados obtidos pelo
algoritmo proposto não foram satisfatórios, porém apresentamos possíveis melhorias
de como deixá-lo mais eﬁciente.
Palavras-chave: Problema do Isomorﬁsmo de Grafos. Emparelhamentos em grafos
bipartidos. Particionamento do conjunto de vértices.
Abstract
In this work we study the Graph Isomorphism Problem and their complexity to
solve it. Our main contribution is to propose an algorithm for the general case of
the Problem, based on partitioning the set vertex and perfect matchings of bipartite
graphs.
We also studied the Brendan McKay’s algorithm, who is the fastest algorithm for
the Graph Isomorphism Problem known. At the end, we implemented the algorithm
proposed in this dissertation and McKay’s algorithm.
After comparison of the two algorithms, we found that the results obtained by the
proposed algorithm were not satisfactory, but improvements are possible as to make
it more eﬃcient.
Key words: Graph Isomorphism Problem. Matchings in bipartite graphs. Partitioning of vertex set.
Agradecimentos
Agradeço primeiramente a Deus, a minha esposa Taís, aos meus pais José e
Maria, ao meu orientador Prof. Dr. Daniel Martin, a UFABC, e todos aqueles que,
direta ou indiretamente me ajudaram na realização deste trabalho.
Conteúdo
1 Introdução
1.1 Objetivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Motivação . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3 Estrutura do trabalho . . . . . . . . . . . . . . . . . . . . . . . . . .
2 Preliminares
2.1 Deﬁnições básicas . . . . . . . . . .
2.1.1 Grafo . . . . . . . . . . . .
2.1.2 Vizinhança e grau . . . . .
2.1.3 Subgrafo . . . . . . . . . . .
2.1.4 Representações de grafos no
2.2 Isomorﬁsmo de grafos . . . . . . .
2.3 Simetrias em grafos . . . . . . . . .
2.4 Problemas computacionais . . . . .
2.4.1 Classes de problemas . . . .
2.4.2 NP-Completo . . . . . . . .
. . . .
. . . .
. . . .
. . . .
plano
. . . .
. . . .
. . . .
. . . .
. . . .
3 Isomorfismo de Grafos
3.1 Problema do Isomorﬁsmo de Grafos .
3.2 Problema do Automorﬁsmo de Grafos
3.3 Relação entre os problemas . . . . . .
3.4 Problema do Isomorﬁsmo de Subgrafos
3.5 Aplicações práticas . . . . . . . . . . .
3.5.1 Impressões digitais . . . . . . .
3.5.2 Zero knowledge proof . . . . .
3.5.3 Aplicações em química . . . . .
3.5.4 Outras aplicações . . . . . . . .
3.6 Revisão bibliográﬁca . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
xi
xi
xii
xii
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
1
2
2
3
4
5
7
8
9
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
11
11
13
13
14
15
15
15
17
17
18
4 Emparelhamentos em grafos bipartidos
4.1 Deﬁnições . . . . . . . . . . . . . . . . . . .
4.2 Encontrando um emparelhamento máximo .
4.3 Enumerando os emparelhamentos perfeitos
4.3.1 Componentes fortemente conexas . .
4.3.2 Gerando novos emparelhamentos . .
4.3.3 Análise de complexidade . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
19
19
20
24
25
29
32
5 Algoritmo para o Problema do Isomorfismo de Grafos
5.1 Simulação . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1.1 Efeitos de uma p-simulação . . . . . . . . . . . .
5.1.2 Partições . . . . . . . . . . . . . . . . . . . . . .
5.1.3 Partição associada a uma rodada . . . . . . . . .
5.1.4 Algoritmo para uma p-simulação . . . . . . . . .
5.1.5 Árvore de partição . . . . . . . . . . . . . . . . .
5.2 Propriedades de uma p-simulação . . . . . . . . . . . . .
5.3 Algoritmo proposto . . . . . . . . . . . . . . . . . . . . .
5.3.1 Emparelhamentos perfeitos e isomorﬁsmo . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
35
36
37
38
39
40
42
44
46
50
6 Algoritmo Pratical Graph Isomorphism
6.1 Rotulação canônica e isomorfo canônico
6.2 Reﬁnamento de partições . . . . . . . .
6.3 Algoritmo de reﬁnamento . . . . . . . .
6.4 Partições aninhadas . . . . . . . . . . .
6.5 Árvore de busca . . . . . . . . . . . . .
6.6 Podando a árvore de busca . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
53
54
55
56
59
59
63
7 Resultados
7.1 Gerador de grafos aleatórios - instâncias positivas
7.1.1 Resultados . . . . . . . . . . . . . . . . .
7.2 Grafos com alto padrão de simetria . . . . . . . .
7.2.1 Grafos fortemente regulares não isomorfos
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
65
66
66
68
68
8 Considerações Finais
8.1 Trabalhos futuros . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
72
Bibliografia
73
9 Anexo
78
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Lista de Figuras
2.1
2.2
2.3
2.4
2.5
2.6
Grafo completo com 4 vértices.
H é subgrafo de G . . . . . . .
Um grafo planar. . . . . . . . .
Dois grafos isomorfos. . . . . .
Hipercubo de dimensão 3. . . .
Um grafo rígido. . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
3
3
4
6
7
4.1
4.2
Grafo dirigido por um emparelhamento perfeito. . . . . . . . . . . .
~ . . . . . . . . .
Componentes fortemente conexas em um digrafo D.
21
26
5.1
5.2
5.3
5.4
5.5
Simulação em um grafo G . . . . . . . . . . . . .
Grafo G rotulado . . . . . . . . . . . . . . . . . .
Árvore de partição. . . . . . . . . . . . . . . . . .
Exemplos de partições. . . . . . . . . . . . . . . .
Exemplo de árvore de recursão do Algoritmo 15.
.
.
.
.
.
37
43
43
49
50
6.1
6.2
Grafo G. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Árvore T (G). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
61
62
7.1
Partição π obtida após uma simulação em um grafo fortemente regular. 70
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Lista de Tabelas
2.1
Um isomorﬁsmo entre G e H. . . . . . . . . . . . . . . . . . . . . . .
7.1
7.2
7.3
7.4
Grafos
Grafos
Grafos
Grafos
aleatórios densos. . . . . . . . . . .
aleatórios esparsos. . . . . . . . . .
fortemente regulares isomorfos. . .
fortemente regulares não isomorfos.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
66
67
68
70
Lista de Siglas
PAG Problema do Automorﬁsmo de Grafos
PGI
Pratical Graph Isomorphism
PIG
Problema do Isomorﬁsmo de Grafos
ZKP
Zero knowledge proof
CAPÍTULO
1
Introdução
1.1
Objetivos
Este trabalho tem como ﬁnalidade estudar o Problema do Isomorﬁsmo de Grafos.
Nesse problema, o conjunto de instâncias válidas são pares {G, H} de grafos ﬁnitos,
e o objetivo é decidir se os grafos G e H são isomorfos, isto é, se possuem a mesma
estrutura subjacente.
A principal contribuição deste trabalho é a proposta de uma nova abordagem
para o Problema do Isomorﬁsmo de Grafos baseada num algoritmo desenvolvido
por McKay [25] em 1981 e que utiliza fortemente o conceito de emparelhamentos em
grafos bipartidos e tópicos relacionados. Nossa proposta consiste em distinguir os
vértices de um grafo através de um processo de simulação e posteriormente utilizar o
resultado dessas simulações para acelerar um algoritmo de força bruta que enumera
mapas entre G e H na busca de um possível isomorﬁsmo entre esses grafos.
O objetivo especíﬁco deste trabalho é apresentar um algoritmo que execute, na
prática, em um tempo razoável. É sabido que os algoritmos conhecidos para o caso
geral do Problema do Isomorﬁsmo de Grafos possuem complexidade de tempo expo-
Capítulo 1. Introdução
xii
nencial, demandando muito tempo de processamento (a complexidade do Problema
e o consumo de tempo dos algoritmos serão abordados no Capítulo 3).
1.2
Motivação
O Problema do Isomorﬁsmo de Grafos tem uma vasta gama de aplicabilidade prática
em diversas áreas de conhecimento, e por isso resolvemos estudá-lo. No Capítulo 3,
mostraremos uma série de aplicações práticas do problema.
1.3
Estrutura do trabalho
Esta monograﬁa, que doravante será chamada de dissertação, está dividida em seis
capítulos, além deste breve capítulo introdutório: o Capítulo 2 introduz os principais
conceitos e deﬁnições da teoria dos grafos que são utilizados ao longo da dissertação.
No Capítulo 3, é apresentado o Problema do Isomorﬁsmo de Grafos, com deﬁnições,
resultados relacionados e aplicações. O Capitulo 4 aborda o conceito de emparelhamentos em grafos bipartidos que servirá de base para o algoritmo apresentado no
Capítulo 5. No Capítulo 6 apresentamos o Algoritmo proposto por McKay, comparando as diferenças e semelhanças com o algoritmo apresentado nesta dissertação.
O último Capítulo 7 apresenta os resultados obtidos, bem como os detalhes da sua
implementação na linguagem C++.
CAPÍTULO
2
Preliminares
2.1
Definições básicas
Neste capítulo serão introduzidas algumas deﬁnições e notações necessárias para
que o problema considerado nesta dissertação seja descrito de forma precisa. Essas
deﬁnições foram baseadas nas referências [18], [34], [22], [28], [6], [5] e [12].
2.1.1
Grafo
Um grafo é um par ordenado (V, E) onde V é um conjunto ﬁnito não vazio, e E é
um conjunto de pares não ordenados de elementos de V . O conjunto V é chamado
de conjunto de vértices 1 , e E de conjunto de arestas. Quando um grafo G não é
deﬁnido de maneira explícita, usa-se V (G) e E(G) para fazer referência aos conjuntos
de vértices e de arestas de G respectivamente.
1
Neste trabalho, é comum supor que o conjunto V é o conjunto de números naturais {1, . . . , n}
para algum n.
Capítulo 2. Preliminares
2.1.2
2
Vizinhança e grau
Se u e v são vértices de um grafo, e a = {u, v} é uma aresta desse grafo, diz-se que
u e v são vizinhos ou vértices adjacentes, ou ainda que estão ligados pela aresta a.
Dizemos ainda que u e v são as pontas ou extremidades da aresta a. O conjunto de
vizinhos de um vértice v num grafo G é denotado por NG (v), ou seja, tem-se
NG (v) = u ∈ V (G) : {u, v} ∈ E(G) .
O grau de um vértice v em um grafo G é o número de vizinhos de v em G, ou seja,
é o número de elementos de NG (v). Denota-se o grau de v por dG (v). Quando o
grafo G puder ser identiﬁcado pelo contexto, denotamos NG (v) e dG (v) simplesmente
por N (v) e d(v) respectivamente. Quando todos os vértices de um grafo possuem
grau d, diz-se que esse grafo é d-regular.
0
1
G
2
3
Figura 2.1: Grafo completo com 4 vértices.
Na Figura 2.1, o grafo G é 3-regular. O grafo completo de ordem n é um grafo
Kn = (V, E), onde V = {1, 2, . . . , n}, que possui todas as arestas, isto é, com
E = {u, v} : {u, v} ⊆ V .
2.1.3
Subgrafo
Um grafo H é um subgrafo de um grafo G se VH ⊆ VG e EH ⊆ EG .
3
2.1. Deﬁnições básicas
2
3
2
3
4
5
1
H
G
4
5
Figura 2.2: H é subgrafo de G
Na ﬁgura 2.2, o grafo H é um subgrafo de G.
2.1.4
Representações de grafos no plano
O objeto grafo leva esse nome porque pode ser representado graﬁcamente de modo
natural. Pode-se representar os vértices de um grafo por pontos no plano, e as
arestas desse grafo por curvas que ligam pares de pontos. Há inﬁnitas maneiras
de se representar um mesmo grafo no plano, e cada uma delas é chamada de uma
imersão no plano.
Um grafo é planar se possui uma imersão no plano de modo que nenhum par de
arestas se cruze.
1
2
K4
4
3
Figura 2.3: Um grafo planar.
Na ﬁgura 2.3 temos um exemplo de um grafo planar. O objetivo deste trabalho
não é estudar representações de grafos no plano, mas esses conceitos serão utilizados
Capítulo 2. Preliminares
4
para ilustrar e exempliﬁcar ideias.
2.2
Isomorfismo de grafos
Os grafos da Figura 2.4 compartilham algumas propriedades entre si (como o número
de vértices e de arestas), dando a impressão que são dois grafos iguais.
1
2
3
G
1
2
3
H
4
5
6
4
5
6
Figura 2.4: Dois grafos isomorfos.
Claramente, esses grafos não são iguais pois seus respectivos conjuntos de arestas
não são os mesmos: G possui a aresta {2, 4} e H não; G possui a aresta {2, 6}
e H não; H possui a aresta {4, 5} enquanto G não a possui. No entanto, pode-se
dizer que, de algum modo, esses grafos compartilham certas propriedades, como
conjunto de vértices e padrão de vizinhanças. A deﬁnição a seguir, que é central
nesta dissertação, formaliza o que acabamos de dizer.
Dois grafos G e H são isomorfos se há uma bijeção ϕ : V (G) → V (H) tal que,
para todo par de vértices i, j ∈ V (G), tem-se
{i, j} ∈ E(G) ⇐⇒ {ϕ(i), ϕ(j)} ∈ E(H).
Uma bijeção com esta propriedade é chamada de isomorfismo. Se G e H são isomorfos, denota-se esse fato pela expressão G ∼
= H.
O conjunto de todos os isomorﬁsmos entre G e H é denotado por Iso(G, H).
5
2.3. Simetrias em grafos
Note que Iso(G, H) é um conjunto de funções.
A Tabela 2.1 mostra um isomorﬁsmo entre os grafos G e H da Figura 2.4.
Tabela 2.1: Um isomorﬁsmo entre G e H.
i
ϕ(i)
1
1
2
5
3
3
4
4
5
2
6
6
Seja G = (V, E) um grafo e seja K o conjunto de todos os pares não ordenados
de V . Então G = (V, K\E) é chamado de grafo complementar de G, ou simplesmente, de complemento de G. É um fato simples que, se G ∼
= H.
= H, então G ∼
2.3
Simetrias em grafos
Alguns grafos, como o da Figura 2.5 são visualmente simétricos2 . O grafo da Figura 2.5 é chamado de cubo. Em geral, um hipercubo de dimensão n é um grafo
Qn = (V, E) onde os conjuntos V e E são dados por
V = {0, 1}n
E = {{u, v} ⊆ V | u difere de v em apenas um bit}
2
O conceito de grafo simétrico será enunciado após o conceito de automorfismo
Capítulo 2. Preliminares
6
000
Q3
010
011
001
100
101
110
111
Figura 2.5: Hipercubo de dimensão 3.
O hipercubo de dimensão n > 3 também é simétrico, embora não seja tão fácil
de se perceber isso pela observação de uma imersão do Qn no plano. Para formalizar o conceito de simetrias em grafos de modo abstrato utilizamos o conceito de
automorﬁsmo.
Um automorfismo de um grafo G = (V, E) é uma permutação3 ϕ : V → V que
preserva as adjacências em G, isto é, que satisfaz
{i, j} ∈ E ⇐⇒ {ϕ(i), ϕ(j)} ∈ E
para todo par de vértices i, j ∈ V .
O conjunto de todos os automorﬁsmos ϕ de um grafo G é denominado Aut(G),
isto é, tem-se
Aut(G) = {ϕ : V → V | ϕ é automorﬁsmo de G}.
Todo grafo possui um automorﬁsmo trivial, a permutação identidade. Se um grafo
3
Uma permutação é uma bijeção de um conjunto nele mesmo.
7
2.4. Problemas computacionais
não possui nenhum automorﬁsmo, exceto o trivial, ele é chamado de grafo rígido.
6
1
2
3
4
5
Figura 2.6: Um grafo rígido.
Um grafo G é não rígido se |Aut(G)| > 1, ou seja, se G não for rígido. Os grafos
das Figuras 2.1 e 2.5 são exemplos de grafos simétricos.
Um grafo G é vértice-transitivo se, dado qualquer par de vértices u, v, há um
automorﬁsmo ϕ : V → V tal que ϕ(u) = v.
Um grafo G é aresta-transitivo se, dados quaisquer dois pares de vértices adjacentes i1 , j1 e i2 , j2 , há um automorﬁsmo ϕ : V → V tal que ϕ(i1 ) = i2 e ϕ(j1 ) = j2 .
Um grafo G é simétrico se é vértice-transitivo e aresta-transitivo.
O conjunto de todas as permutações de {1, 2, . . . , n} é denotado por Sn . O grafo
completo com n vértices é um exemplo de grafo para o qual Aut(G) = Sn .
Dado um grafo G = (V, E) e uma função injetora ϕ : V → V , denotamos por
ϕ(G) o grafo deﬁnido por
ϕ(G) = (V, ϕ(E))
onde ϕ(E) = {ϕ(u), ϕ(v)} : {u, v} ∈ E(G) .
2.4
Problemas computacionais
As deﬁnições4 que se seguem foram baseadas nas referências [18] e [33].
4
Estas definições são baseadas em um modelo computacional de Turing
Capítulo 2. Preliminares
8
Um alfabeto é um conjunto ﬁnito cujos elementos são chamados de símbolos. Uma
palavra sobre um alfabeto Σ é uma sequência ﬁnita de símbolos de Σ. O comprimento
de uma palavra w é o número de elementos da sequência w e é denotado por |w|. O
conjunto de todas as palavras sobre Σ é denominado Σ∗ . Uma linguagem sobre um
alfabeto Σ é um subconjunto de Σ∗ .
Em computação, um tipo de problema muito estudado é o problema de decisão.
Problemas desse tipo admitem apenas as respostas sim ou não. Por exemplo, descobrir se uma página na web contêm o texto “index of” é um problema de decisão;
descobrir se a conectividade de uma rede de computadores é tolerante à falha de k
máquinas nessa rede é outro problema de decisão.
Todo problema de decisão em computação corresponde ao problema de se decidir
se uma dada palavra w sobre um alfabeto Σ pertence ou não a uma linguagem L.
Neste trabalho, os termos linguagem e problema se referem ao mesmo conceito. Por
isso, quando se diz que um algoritmo A decide uma linguagem L, o que se quer dizer
é que o algoritmo A, ao receber uma palavra w como entrada, devolve corretamente
sim caso w ∈ L e não caso w 6∈ L.
2.4.1
Classes de problemas
Classiﬁcamos os problemas de decisão em classes de complexidade de acordo com
a quantidade de recursos5 necessários para resolvê-los. Embora existam diversas
classes de complexidade, este trabalho apenas faz referência às classes P e NP, que
serão deﬁnidas a seguir (conforme [18]).
Uma linguagem L pertence à classe P se existe um polinômio p(n) e um algoritmo
que decide L cujo tempo total de execução com entrada w (até uma resposta sim
ou não) não ultrapassa p(|w|).
Uma linguagem L está na classe NP se e somente se há uma linguagem A ∈ P
5
As definições apresentadas são aplicadas ao modelo computacional de Turing.
9
2.4. Problemas computacionais
e um polinômio p(n) tal que, para toda palavra x ∈ Σ∗ , tem-se x ∈ L se e somente
se existe y ∈ Σ∗ com |y| ≤ p(|x|) tal que (x, y) ∈ A. A palavra y é chamada de um
certificado para x ∈ L.
Sejam A e B duas linguagens. Dizemos que A é Turing-redutível a B em tempo
polinomial (escreve-se A ≤pT B) se existe um algoritmo que decide A, que executa
em tempo polinomial, e que pode ter instruções condicionais na forma
se y ∈ B então . . . senão . . . ﬁm.
onde considera-se (para o cômputo do consumo de tempo do algoritmo) que uma
consulta da forma y ∈ B leva tempo constante.
2.4.2
NP-Completo
Uma linguagem L é NP-Completo se L ∈ NP e toda linguagem em NP é Turingredutível a L. Esta classe é de suma importância para o entendimento do problema
P versus NP, pois haverá um algoritmo em tempo polinomial para um problema NPCompleto se e somente se todo problema em NP possuir um algoritmo em tempo
polinomial que o resolva. Em outras palavras, se houver um algoritmo polinomial
para um problema NP-Completo, então P = NP. Como há evidências que P e NP
são diferentes, a prova de que um problema é NP-Completo é considerada uma forte
evidência desta intratabilidade.
CAPÍTULO
3
Isomorfismo de Grafos
Neste capítulo, apresentamos dois problemas computacionais: o Problema do Isomorﬁsmo de Grafos e o Problema do Automorﬁsmo de Grafos. Daremos também
algumas aplicações do Problema do Isomorﬁsmo em situações práticas.
3.1
Problema do Isomorfismo de Grafos
Deﬁnimos a versão de decisão para o Problema do Isomorﬁsmo de Grafos (PIG)
do seguinte modo: dado um par de grafos {G, H}, decidir se esse par pertence ao
conjunto
I = {G, H} | G é isomorfo a H .
Um algoritmo para a versão de decisão do PIG retorna sim se os grafos da entrada
forem isomorfos e não caso contrário.
O melhor algoritmo conhecido para o PIG é o proposto por Babai e Luks em [4],
Capítulo 3. Isomorﬁsmo de Grafos
√
que possui tempo de execução 2O(
n log n) ,
12
onde n é o número de vértices. Foggia [10]
comparou os algoritmos propostos por Ullmann [36], Cordella[11], McKay [25] e
Schimidt [32], e concluiu que o algoritmo implementado no programa Nauty (e
elaborado por B. McKay [25]) é o mais rápido na prática. Em [35], Torán demonstrou
que o PIG é pelo menos tão difícil quanto o problema de se computar o determinante
de uma matriz com entradas inteiras.
Existem algoritmos que decidem casos especiais do PIG em tempo polinomial.
Tais algoritmos existem para: árvores [18], grafos planares [15], grafos de intervalo
[20], grafos de permutação [7], grafos de genus limitado [26], grafos de grau limitado
[21], e grafos cujos autovalores possuem multiplicidade limitada [3]. No entanto, não
se conhece nenhum algoritmo eﬁciente para o caso geral e portanto não se sabe se
o PIG está na classe P ou se é NP-Completo [16], embora suspeita-se que ele esteja
estritamente entre as duas classes [2]. Por outro lado, dados dois grafos G e H e um
mapa ϕ entre seus conjuntos de vértices, há um algoritmo polinomial que decide se
ϕ é um isomorﬁsmo entre os grafos dados.
Algoritmo 1: Um veriﬁcador para o PIG
Entrada: Grafos G e H com mesmo número de vértices, e função injetora
ϕ : V (G) → V (H)
Saída: sim se ϕ(G) = H e não caso contrário
início
para todo u ∈ V faça
para todo v ∈ V faça
se {u, v} ∈ E(G) e {ϕ(u), ϕ(v)} ∈
/ E(H) então
retorna não
fim se
se {u, v} ∈
/ E(G) e {ϕ(u), ϕ(v)} ∈ E(H) então
retorna não
fim se
fim para todo
fim para todo
retorna sim
fim
13
3.2. Problema do Automorﬁsmo de Grafos
Conforme a deﬁnição de certiﬁcado, (vide seção 2.4.1), sabemos que o PIG pertence à classe NP. Para demonstrar tal aﬁrmação, considere a linguagem
A = ({G, H}, ϕ) : G, H são grafos e ϕ ∈ Iso(G, H)
Note que {G, H} ∈ P IG ⇔ ({G, H}, ϕ) ∈ A. Ademais, A ∈ P pois o Algoritmo 1 decide A e é claramente polinomial. Note também que qualquer mapeamento ϕ : V (G) → V (H) pode ser representado usando tamanho O(n). Com isso,
podemos concluir que PIG ∈ NP.
3.2
Problema do Automorfismo de Grafos
Seja G um grafo. Decidir se o grupo de automorﬁsmos de G possui algum automorﬁsmo diferente do trivial é um problema de decisão chamado Problema do Automorﬁsmo de Grafos (PAG), e consiste em determinar se G pertence ao conjunto
A = {G : |Aut(G)| > 1}.
Assim como o PIG, o Problema do Automorﬁsmo de Grafos também pertence à
classe NP [18].
3.3
Relação entre os problemas
Podemos mostrar que o PAG é Turing-redutível ao PIG. Antes de mostrarmos a
redução, precisamos da seguinte deﬁnição: G[i] é o grafo obtido de G ligando ao
vértice i um caminho com |V (G)| + 1 novos vértices. O propósito desta construção
é que todo automorﬁsmo deste grafo modiﬁcado mapeia o vértice i em si mesmo, e
além disso, não ocorre no grafo modiﬁcado nenhum automorﬁsmo que não estivesse
Capítulo 3. Isomorﬁsmo de Grafos
14
presente no grafo original (isto é, Aut(G[i] ) ⊆ Aut(G)).
A ideia central da Turing-redução apresentada no Algoritmo 2 é a seguinte: se os
grafos G e H são isomorfos, e existe um isomorﬁsmo ϕ de G em H tal que v = ϕ(u),
então os grafos G[u] e H[v] também são isomorfos. O Algoritmo 2 computa o PAG
em tempo polinomial fazendo consultas de decisão ao PIG como descrito a seguir.
Algoritmo 2: Algoritmo para o PAG usando consultas ao PIG
Entrada: Grafo G com conjunto de vértices {1, 2, . . . , n}
Saída: sim se |Aut(G)| > 1 e não se G é rígido
início
para i ← 1 até n − 1 faça
para j ← i + 1 até n faça
se {G[i] , G[j] } ∈ PIG então
retorna sim
fim se
fim para
fim para
retorna não
fim
Retomando a demonstração da corretude da Turing-redução, o grafo G possui
um automorﬁsmo não trivial se, e somente se, G tem um automorﬁsmo que mapeia
i em j para algum par de vértices i 6= j. Pela observação no parágrafo que precede o
Algoritmo 2, um automorﬁsmo que mapeia i em j existe se, e somente se, os grafos
G[i] e G[j] são isomorfos. Como o algoritmo testa todas as possíveis combinações
de diferentes vértices i e j, ele consegue determinar, em tempo O(n2 ) se o grafo
de entrada é rígido ou não. Portanto P AG ≤pT P IG. Atualmente não se conhece
nenhuma Turing-redução do PIG ao PAG [18].
3.4
Problema do Isomorfismo de Subgrafos
Dados dois grafos G e H, o Problema do Isomorﬁsmo de Subgrafos consiste em
decidir se H é isomorfo a algum subgrafo de G, ou seja, se H pode ser transformado
15
3.5. Aplicações práticas
em um subgrafo de G apenas renomeando-se seus vértices. Este problema é uma
generalização do PIG e pertence à classe dos problemas NP-Completos, que são os
problemas mais difíceis da classe NP [37].
3.5
Aplicações práticas
Nesta seção, destacaremos algumas aplicações práticas onde o problema de isomorﬁsmo de grafos é utilizado.
3.5.1
Impressões digitais
Nandi [27] utiliza o PIG para confrontar imagens de impressões digitais, que são
representadas por grafos gerados pelas características presentes em cada imagem.
Cada uma dessas características representa um vértice no grafo, e as arestas representam as relações que estas características possuem entre si. Para veriﬁcar se
uma impressão digital corresponde a outra, resolve-se uma instância do Problema
do Isomorﬁsmo dos Grafos. Para essa aplicação, seria desejada a existência de um
algoritmo polinomial para o PIG ou que as instâncias geradas a partir das imagens
de impressões digitais fossem grafos de uma das classes onde o PIG é solúvel em
tempo polinomial (como aquelas listadas na Seção 3.1).
3.5.2
Zero knowledge proof
Sistemas de zero knowledge proof 1 tem aplicações em criptograﬁa e protocolos de
segurança que requerem autenticação. Uma dessas aplicações, que se baseia na
diﬁculdade de se resolver o PIG, é descrita a seguir.
Um agente P conhece um circuito Hamiltoniano C em um grafo G, e um outro agente, chamado Q, conhece o grafo G mas não o circuito Hamiltoniano. O
1
Adaptado de [18] e [13]
Capítulo 3. Isomorﬁsmo de Grafos
16
agente Q está disposto a pagar uma grande quantia em dinheiro pelo circuito Hamiltoniano2 C, porém, antes de fazer o pagamento, ele precisa se certiﬁcar de que
P realmente conhece o circuito Hamiltoniano que diz conhecer. O agente P, por sua
vez, precisa provar a Q que conhece o circuito C sem revelá-lo, pois se o revelar a
Q, este poderá ser desonesto e não fazer o pagamento, uma vez que já adquiriu o
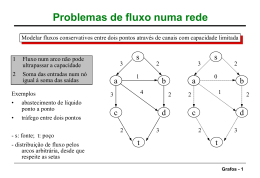
objeto de seu desejo.
Os dois começam, então, um jogo no qual, em cada rodada, P escolhe uma permutação qualquer ϕ : V (G) → V (G) e cria um grafo H = ϕ(G) (que é claramanete
isomorfo a G) e o envia a Q. Note que, se P conhece um circuito Hamiltoniano C
em G, então ele também conhece um em H, a saber, o circuito ϕ(C). Em seguida,
Q solicita a P que revele exatamente uma dentre duas coisas: ou o isomorﬁsmo ϕ
entre G e H, ou um circuito Hamiltoniano em H. Se Q solicitou um isomorﬁsmo,
então P mostra o mapeamento ϕ e Q veriﬁca que, de fato, este mapeamento é um
isomorﬁsmo de G em H. Se Q solicitou o circuito, P mostra o circuito ϕ(C) em H.
As respostas de P não revelam o ciclo Hamiltoniano original em G (a menos
que Q seja tão poderoso computacionalmente que consiga resolver o PIG). A cada
rodada, Q saberá apenas o isomorﬁsmo de H em G ou um circuito Hamiltoniano
em H, mas nunca ambos numa mesma rodada. Ele precisaria de ambas as respostas
na mesma rodada a ﬁm de descobrir o circuito em G; assim, a informação permanece
protegida.
Para ser capaz de responder às duas perguntas corretamente, P deve conhecer
um isomorﬁsmo entre G e H e também um circuito Hamiltoniano em H (e portanto
também em G). Suponhamos agora que P não conheça um circuito Hamiltoniano
e esteja tentando enganar Q para ﬁcar com o dinheiro. A cada rodada, P não sabe
qual pergunta lhe será feita até enviar H para Q. O agente P pode tentar adivinhar
qual pergunta Q irá fazer e gerar o grafo H de acordo. Se P acha que Q irá lhe
2
Um circuito é Hamiltoniano quando vértice é visitado apenas uma vez.
17
3.5. Aplicações práticas
perguntar um isomorﬁsmo ele pode gerar um grafo H isomorfo a G. Nesse caso,
suas más intenções seriam descobertas caso Q lhe ﬁzesse a outra pergunta pois ele
não conhece um circuito Hamiltoniano em G (e portanto também não o conhece
em H). Se P acha que Q irá lhe perguntar por um circuito Hamiltoniano ele pode
tentar gerar um grafo H que tenha um tal circuito, mas seria desmascarado caso Q
lhe pedisse por um isomorﬁsmo.
Com isso, se Q escolhe a pergunta aleatoriamente com probabilidade 1/2, a
chance de P enganar Q é de 2−n , onde n é o número de rodadas. Portanto, após um
número razoável de rodadas, Q se convence, com um alto grau de conﬁabilidade, de
que P de fato conhece um circuito Hamiltoniano em G.
Observa-se que, enquanto a primeira aplicação seria beneﬁciada caso PIG ∈
P , a segunda perderia completamente seu sentido, pois baseia-se na diﬁculdade
computacional de se decidir a linguagem PIG.
3.5.3
Aplicações em química
Para se determinar se uma molécula possui uma estrutura similar a uma outra, é
necessário fazer uma comparação desta molécula com um banco de dados de moléculas existentes. Cada molécula é representada por um grafo, onde os vértices são os
átomos e as arestas correspondem às ligações atômicas. O processo de comparação
consiste em veriﬁcar se as estruturas moleculares são idênticas, ou seja, se os grafos
que representam duas moléculas são isomorfos [30].
3.5.4
Outras aplicações
O autor Conte [8] utiliza o PIG para o reconhecimento de padrões. Já Farouk [9]
trabalha com o reconhecimento de imagens e Pedarsani [29], em seu artigo, trata da
segurança de informação em redes sociais, todos utilizam o PIG para a resolução de
seus problemas.
Capítulo 3. Isomorﬁsmo de Grafos
3.6
18
Revisão bibliográfica
Para a realização desta pesquisa foram consultados diversos trabalhos, entre artigos
e dissertações. O primeiro a ser destacado é o artigo escrito por McKay [25], onde o
autor apresenta um algoritmo para o PIG. Este algoritmo determina uma representação canônica dos grafos utilizando um particionamento ordenado de seus vértices.
Todos os vértices de uma partição possuem uma mesma rotulação, distinguindo-os
dos demais vértices do grafo. Este particionamento é calculado aplicando-se um conjunto de invariantes de vértices a uma primeira partição, que, inicialmente, agrupa
todos os vértices do grafo. Ao ﬁnal do processo, dois grafos são isomorfos se, e
somente se, possuem a mesma representação. No Capítulo 6 descreveremos com
maiores detalhes o algoritmo proposto por McKay.
Para obter o referencial teórico do Problema do Isomorﬁsmo de Grafos, foi estudado o livro de Köbler, Schöning e Torán [18]. Este livro traz as deﬁnições do
PIG e do PAG, apresenta quais problemas computacionais são redutíveis ao PIG,
e apresenta uma abordagem muito detalhada do PIG do ponto de vista de sua
complexidade.
CAPÍTULO
4
Emparelhamentos em grafos bipartidos
O algoritmo que será proposto no Capítulo 5 utiliza emparelhamentos em um grafo
bipartido para a veriﬁcação do isomorﬁsmo entre dois grafos G e H. Portanto, neste
capítulo vamos apresentar o conceito de emparelhamento, e também um método
eﬁciente para enumerar todos os emparelhamentos perfeitos de um grafo bipartido.
4.1
Definições
Um grafo G é chamado bipartido se seu conjunto de vértices V pode ser dividido em
dois conjuntos disjuntos V1 e V2 , onde toda aresta de G é da forma {u, v} com u ∈
V1 , v ∈ V2 .
Dado um grafo G, um emparelhamento M em G é um conjunto de arestas disjuntas duas a duas. Um vértice é dito saturado (ou coberto) por M quando é incidente
a uma aresta do emparelhamento. Um emparelhamento M é dito: perfeito quando
todos os vértices estão saturados; maximal quando não há nenhum emparelhamento
Capítulo 4. Emparelhamentos em grafos bipartidos
20
M ′ que contenha propriamente M ; e máximo se não existe um emparelhamento
com maior número de arestas que M . Observe que todo emparelhamento perfeito é
máximo.
Um caminho em um grafo é chamado de caminho alternante em relação a um
emparelhamento M (ou M -alternante) se, para quaisquer duas arestas consecutivas
desse caminho, uma está em M e a outra não. Um caminho alternante é dito
caminho aumentante em relação a M (ou M -aumentante) quando o primeiro e o
último vértice não estão saturados por M .
~ é um par ordenado (V, A) onde V é um conjunto
Um grafo dirigido (ou digrafo) G
ﬁnito de vértices e A é um conjunto de pares ordenados de V chamados arcos. Seja
~ dizemos que u é o vértice de partida e v o vértice de chegada
a = (u, v) um arco de G,
de a. Dizemos ainda que o arco a é orientado de u para v. A vizinhança de saída
~ : (u, v) ∈ A(G)}.
~
de um vértice u é o conjunto N + (u) = {v ∈ V (G)
Dados um grafo bipartido G = (V1 ∪ V2 , E) e um emparelhamento M de G,
~ = D(G,
~
~ =
deﬁnimos o digrafo associado como sendo o digrafo D
M ), onde V (D)
~ é o conjunto de arcos que é obtido orientando-se as arestas de M de
V (G) e A(D)
V1 para V2 e as arestas de E \ M no sentido oposto. A Figura 4.1 nos mostra um
exemplo de um grafo bipartido G, de um emparelhamento perfeito M em G e do
~
digrafo associado D(G,
M ).
4.2
Encontrando um emparelhamento máximo
Nesta seção, apresentamos um algoritmo para encontrar um emparelhamento máximo em um grafo bipartido. Porém, antes de apresentarmos tal algoritmo, vamos
enunciar o Teorema de Berge1 , que será importante para seu entendimento.
Teorema 1. Um emparelhamento M de um grafo G é máximo se e somente se não
1
Adaptado de [17] e [31]
21
4.2. Encontrando um emparelhamento máximo
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
G
M
~
D(G,
M)
Figura 4.1: Grafo dirigido por um emparelhamento perfeito.
existe um caminho M -aumentante em G.
Demonstração. Se existe um caminho M -aumentante P , podemos criar um emparelhamento maior eliminando as arestas de M que pertencem a P e incluindo as
arestas de P que originalmente não pertençam a M . Note que esta permuta de
arestas corresponde a tomar o emparelhamento2 M ∆P . Para provar a recíproca,
suponhamos que M não é máximo. Portanto, existe um outro emparelhamento M ′
com mais arestas que M . Considere o grafo H deﬁnido por H = (V (G), M ∆M ′ ).
Cada vértice v ∈ V (H) tem grau 0, 1 ou 2 porque v pode ser incidente em, no
máximo, uma aresta de M e uma de M ′ . As componentes conexas de H podem
2
O símbolo ∆ denota a operação de diferença simétrica entre dois conjuntos.
Capítulo 4. Emparelhamentos em grafos bipartidos
22
então ser: ou vértices isolados, ou circuitos de ordem par3 com arestas alternadas
de M e de M ′ , ou ainda caminhos com arestas alternadas de M e de M ′ . Como
|M ′ | > |M |, o grafo H tem mais arestas de M ′ que de M e, portanto, pelo menos
uma das componentes de H é um caminho que começa e termina com arestas de M ′
(e que não pertencem a M ); esse caminho é um caminho M -aumentante no grafo
G. Isso encerra a prova do teorema.
Com base no conceito de caminho M -aumentante e no Teorema 1, podemos desenvolver um algoritmo que encontra um emparelhamento máximo (Algoritmo 3).
A ideia do algoritmo é encontrar caminhos M -aumentantes e fazer a permuta das
arestas de M com as arestas dos caminhos encontrados. A busca por caminhos
aumentantes e a permuta de arestas são realizadas sucessivamente até que o emparelhamento corrente seja máximo4 . Vamos usar S para denotar o conjunto de
vértices saturados.
O algoritmo tem como entrada um grafo G e um emparelhamento inicial M , que
~
pode ser vazio. Note que, caso M = ∅, todas os arcos de D(G,
M ) serão orientados
em um único sentido. Quanto maior for o emparelhamento inicial M , mais rápido o
algoritmo encontra um emparelhamento máximo.
Em seguida, para todo vértice a ∈ V1 não saturado, é realizada uma busca em
profundidade, e é obtido um caminho dirigido P entre a e um vértice não saturado
b ∈ V2 . O vértice a é não saturado pela própria escolha de a (na linha 8 do Algoritmo 3) e b é não saturado pois é o vértice devolvido pelo algoritmo de busca
em profundidade (Algoritmo 4), que possui justamente como critério de parada encontrar um vértice não saturado em V2 (veja linha 2). Note que P é um caminho
M -aumentante, pois começa em a e termina em b[a], que são ambos não saturados.
3
4
Circuitos que possuem um número par de arestas.
Este algoritmo é uma adaptação do algoritmo de Hopcroft-Karp, disponível em [14]
23
4.2. Encontrando um emparelhamento máximo
Algoritmo 3: Encontrar emparelhamento máximo de um grafo G
Entrada: Grafo bipartido G = (V1 ∪ V2 , E), emparelhamento M
1 início
2
S ← {v ∈ V1 ∪ V2 : v incide em alguma aresta de M }
~ ← D(G,
~
3
D
M)
4
repita
~
5
para todo v ∈ D(G)
faça
6
pai[v] ← N U LL
7
fim para todo
8
para todo a ∈ V1 \ S faça
9
pai[a] = a
10
b[a] ← Busca(a)
11
fim para todo
12
para todo a ∈ V1 \ S faça
13
se b[a] 6= N U LL então
14
Inverte(b[a])
15
S ← S ∪ {a, b[a]}
16
fim se
17
fim para todo
18
até até que a cardinalidade de S não aumente;
19 fim
Uma vez encontrado o caminho M -aumentante P de a até b, o emparelhamento M é substituido por M ∆P . Essa atualização do emparelhamento é feita de
modo implícito, invertendo-se a orientação dos arcos no caminho P (através de uma
~ é, na realidade, D(G,
~
M ∆P ).
chamada ao Algoritmo 5). Desse modo o novo grafo D
O laço entre as linhas 4 e 18 do Algoritmo 3 é executado até que não seja mais
possível saturar nenhum novo vértice, ou seja, até que nenhum outro caminho M aumentante possa ser encontrado. Quando isto ocorre, pelo Teorema 1, temos que
M é máximo.
Capítulo 4. Emparelhamentos em grafos bipartidos
24
Algoritmo 4: Busca
Entrada: vértice u
Saída: vértice b ou N U LL
1 início
2
se u ∈ V2 e N + (u) = ∅ então
3
retorna u
4
fim se
5
para todo v ∈ N + (u) faça
6
se pai[v] = N U LL então
7
pai[v] ← u
8
b ← Busca(v)
9
se b 6= N U LL então
10
retorna b
11
fim se
12
fim se
13
fim para todo
14
retorna N U LL
15 fim
4.3
Enumerando os emparelhamentos perfeitos
Nesta seção apresentamos um algoritmo que enumera os emparelhamentos perfeitos
em um grafo bipartido G, baseado no algoritmo proposto por Uno [38]. Seja G
~ = D(G,
~
um grafo bipartido, M um emparelhamento perfeito de G e D
M ) o grafo
dirigido associado. Podemos obter um novo emparelhamento de G permutando
arestas de M com arestas presentes em um circuito ou em caminhos M -alternantes
~ Em outras palavras, o grafo gerado pela diferença simétrica de M com um
de D.
emparelhamento diferente é composta por circuitos, caminhos alternantes ou vértices
isolados.
Como em um emparelhamento perfeito todos os vértices estão saturados, o grafo
gerado pela diferença simétrica entre dois emparelhamentos perfeitos é composta
apenas por circuitos alternantes e vértices isolados. Portanto, um grafo G possuirá
~
emparelhamentos perfeitos diferentes de M somente se o digrafo D(G,
M ) possuir
circuitos alternantes. Portanto, a ideia central do Algoritmo 9 é encontrar um cir-
25
4.3. Enumerando os emparelhamentos perfeitos
Algoritmo 5: Inverte
Entrada: vértice b
1 início
2
x←b
3
enquanto pai[x] 6= x faça
~
4
Remover arco (pai[x], x) de D
~
5
Inserir arco (x, pai[x]) em D
6
x ← pai[x]
7
fim enquanto
8 fim
~ no digrafo D(G,
~
cuito dirigido C
M ) e permutar suas arestas com as arestas emparelhamento perfeito M . Essa permuta irá gerar um novo emparelhamento perfeito
~ Um modo de se encontrar um circuito dirigido em D
~ seria fazer uma
M ′ = M ∆C.
~ buscando uma aresta de retorno [19]. Uma outra
busca em profundidade no grafo D,
~ em componentes fortemente conexas (este assunto será abormaneira é decompor D
dado na próxima seção). Este método é mais eﬁciente em relação ao primeiro pois
é possível encontrar todos os circuitos com apenas duas buscas em profundidade.
4.3.1
Componentes fortemente conexas
~ = (V, A) é um subconjunto
Uma componente fortemente conexa de um digrafo G
~ tal que, para todo par de vértices u e v em S, há um
maximal de vértices S ⊆ V (G)
~ é o grafo G
~ T = (V, AT ) onde
caminho de u a v e vice-versa. O grafo transposto de G
AT = (u, v) : (v, u) ∈ A(G)) . A Figura 4.2 apresenta as componentes fortemente
~
conexas de um digrafo D.
Os conceitos de circuito dirigido e componentes fortemente conexas estão associados, visto que um arco está em um circuito dirigido se e somente se suas extremidades
estão em uma mesma componente fortemente conexa. De fato, sejam u e v vértices
~ Como u, v ∈ F , haverá
e F uma componente fortemente conexa de um digrafo G.
um caminho P de u até v e um caminho P ′ de v até u. Com isso, é fácil veriﬁcar
Capítulo 4. Emparelhamentos em grafos bipartidos
26
que P ∪ P ′ contém um circuito. Portanto, um modo de se encontrar um circuito
~ no grafo D(G,
~
~ em
C
M ) é executar um algoritmo que particiona os vértices de D
componentes fortemente conexas e, em seguida, veriﬁcar quais arcos pertencem a
uma mesma componente fortemente conexa.
Suponha que um arco e não pertença a nenhum circuito. Podemos excluir o
~ pois ele será irrelevante para encontrarmos um emparelhamento
arco e do digrafo D
~ Vamos
perfeito M ′ . Neste ponto, suponha que o arco e tenha sido removido de D.
analisar os dois casos possíveis para o arco e: em primeiro lugar, se e ∈ M , então
e estará presente também em M ′ = M ∆C. No segundo caso, se e ∈
/ M , então
~ não teve relevância para
e∈
/ M ′ = M ∆C. Em ambos os casos, a presença de e em D
encontrarmos um novo emparelhamento perfeito M ′ . Portanto, podemos excluir e
~ sem nenhum prejuízo ao emparelhamento M ′ .
de D
0
1
2
3
4
5
6
7
~
D
~
Figura 4.2: Componentes fortemente conexas em um digrafo D.
~ mas
Como não estamos apenas interessados em encontrar um circuito em D,
~ todos os arcos que não pertencem a circuitos, é
também em eliminar do grafo D
~ Para tanto, optamos por utilizar um
importante encontrar todos os circuitos de D.
~ em
algoritmo (com custo de tempo linear, ou seja, O(|V | + |E|)) que particione D
componentes fortemente conexas. Na próxima seção vamos apresentar um algoritmo
~ os
que faça essa decomposição e na Seção 4.3.2 vamos explicar como remover de D
27
4.3. Enumerando os emparelhamentos perfeitos
arcos que não estão em circuitos usando componentes fortemente conexas.
Algoritmo para decomposição em componentes fortemente conexas
O Algoritmo 6 decompõe um digrafo em suas componentes fortemente conexas5 , e
depende dos Algoritmos 7 e 8, que executam uma busca em profundidade a partir
de um conjunto ordenado de vértices.
Algoritmo 6: ComponentesFortementeConexas
~
Entrada: Digrafo G
Saída: Vetor C2
1 início
~
2
F0 ← ordem qualquer dos vértices de V (G)
~ F0 )
3
(F1 , C1 ) ← DFS(G,
~ T , F1 )
4
(F2 , C2 ) ← DFS(G
5
retorna C2
6 fim
Nos Algoritmos 7 e 8 temos um vetor chamado pai, que é utilizado para guardar
as árvores de uma ﬂoresta de busca em profundidade. Para todo nó v em uma árvore
de busca, o nó pai de v estará armazenado em pai[v]. Deﬁnimos também que os
vértices ainda não explorados pela busca em profundidade recebem o valor N U LL
como pai e um vértice raiz de uma árvore de busca terá a si mesmo como pai.
Temos também nos Algoritmos 7 e 8 um estrutura do tipo ﬁla, denominada F ,
que armazena os vértices na ordem em que eles foram explorados na busca em profundidade. Note que, na linha 10 do Algoritmo 7 e nas linhas 7 e 10 do Algoritmo 8
temos uma operação de concatenação (representada pelo símbolo ·) entre um vértice
e uma lista de vértices ou entre duas listas de vértices. Observe que ao percorrer~ ordenados pelo momento
mos a ﬁla F do ﬁm para o início, temos os vértices de G
5
Adaptado de [19]
Capítulo 4. Emparelhamentos em grafos bipartidos
28
Algoritmo 7: DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
~ lista de vértices L
Entrada: Digrafo G,
Saída: Vetor C e Fila F
início
F ←∅
~ elementos
C ← novo vetor com |V (G)|
~ faça
para todo u ∈ V (G)
pai[u] ← N U LL
fim para todo
k←0
para todo u ∈ L faça
se pai[u] = N U LL então
pai[u] ← u
F ← DFSVISIT(u, C) · F
k ←k+1
fim se
fim para todo
retorna F, C
fim
em que foram explorados pelo algoritmo de busca em profundidade (vértices mais a
esquerda tiveram sua exploração ﬁnalizada por último).
Na linha 11 do Algoritmo 7, k é um contador de componentes da ﬂoresta de
~ Ao se encerrar a exploração de uma árvore na ﬂoresta de busca
busca do digrafo G.
em profundidade, o contador k é incrementado (observe que cada árvore na ﬂoresta
da busca inicializada na linha 4 do Algoritmo 6 está associada a uma componente
fortemente conexa) e, ao se iniciar a exploração em uma nova árvore enraizada por
u, o Algoritmo 8 armazena no vetor C a componente fortemente conexa na qual u
e seus descendentes v pertencem (veja linha 3).
~ Como todo
Sejam n o número de vértices e m o número de arcos do digrafo G.
vértice u deve ser explorado pela busca em profundidade, temos n chamadas ao
Algoritmo 8 (muitas delas recursivas). Em cada chamada, todo vértice v ∈ N + (u)
será testado. No total, o número de testes realizados será igual ao número de arcos.
29
4.3. Enumerando os emparelhamentos perfeitos
Algoritmo 8: DFSVISIT
Entrada: vértice u, vetor C
Saída: Vértice u concatenado com a Fila F
1 início
2
F ←∅
3
C[u] ← k
4
para todo v ∈ N + (u) faça
5
se pai[v] = N U LL então
6
pai[v] ← u
7
F ← DFSVISIT(v, C) · F
8
fim se
9
fim para todo
10
retorna u · F
11 fim
O tempo total gasto para as chamadas ao Algoritmo 8 é O(m). Devemos acrescentar
também o tempo gasto para inicialização do vetor pai (linhas 3 a 5 do Algoritmo
7) e o tempo gasto para se veriﬁcar se o vértice s já foi explorado pela busca em
profundidade (linha 8 do Algoritmo 7). Ao todo, isso leva tempo O(n). Portanto, o
tempo de execução6 do Algoritmo 7 é O(n + m).
4.3.2
Gerando novos emparelhamentos
~ serão ou
Note que, após a decomposição, as componentes fortemente conexas de D
~ ou estarão em um circuito
vértices isolados ou circuitos. Portanto, os arcos de D
ou terão seus vértices de partida e chegada localizados em componentes fortemente
conexas diferentes. O Algoritmo 11 se utiliza desta propriedade para eliminar todos
os arcos que não pertencem a nenhum circuito pois, como veremos mais adiante,
apenas arcos que estejam em um circuito são utilizados para se encontrar novos
emparelhamentos (linha 8 do Algoritmo 9 e linhas 10 e 13 do Algoritmo 10.
Em uma descrição informal, o Algoritmo 9 recebe inicialmente um emparelha~ = D(G,
~
M ) e escolhe um
mento perfeito M (obtido pelo Algoritmo 3) e o digrafo D
6
Para mais explicações e verificação da corretude do algoritmo, consulte [19]
Capítulo 4. Emparelhamentos em grafos bipartidos
30
~ que também pertença a M . No próximo passo, é
arco arbitrário e = (u, v) de D,
~ contendo e, e é construído um emparelhamento perfeito
encontrado um circuito C,
M ′ = M ∆C. Depois, o algoritmo gera dois novos digrafos: o primeiro é obtido
excluindo-se os vértices u e v e os arcos que incidem neles; o segundo é obtido
excluindo-se o arco e. Em ambos os digrafos obtidos, os arcos que não pertencem
a um circuito são excluídos do digrafo. Por ﬁm, o algoritmo realiza uma chamada
recursiva para cada grafo gerado. Veremos com maiores detalhes o funcionamento
do algoritmo após enunciá-lo.
Com base nas deﬁnições acima, e no algoritmo de decomposição em componentes
fortemente conexas, podemos então mostrar o Algoritmo 9, que enumera todos os
emparelhamentos perfeitos em um grafo bipartido.
Algoritmo 9: Enumerar Emparelhamentos Perfeitos
Entrada: Grafo bipartido G
1 início
2
Encontrar um emparelhamento perfeito M de G pelo Algoritmo 3
3
se M não existe então
4
Fim
5
fim se
6
Imprimir M
~ ← D(G,
~
7
D
M)
~
8
EliminarArestasDesnecessarias (D)
~ M ).
9
EnumEmpPerfeitosRecursivo (D,
10 fim
Primeiramente o Algoritmo 9 veriﬁca se há um emparelhamento perfeito no grafo
dado utilizando o Algoritmo 3. Caso exista, inicia-se o processo de listar todos os
emparelhamentos perfeitos, procurando um circuito C, M -alternante, e gerando um
novo emparelhamento perfeito M ′ = M ∆C. O próximo passo é escolher um arco e
que esteja tanto em M quanto no circuito C. Observe que e está em M mas não
31
4.3. Enumerando os emparelhamentos perfeitos
Algoritmo 10: EnumEmpPerfeitosRecursivo
~ M
Entrada: D,
1 início
~ = ∅ então
2
se D
3
Fim
4
fim se
5
Encontrar um circuito M -alternante C
6
Escolher uma aresta arbitrária e ∈ C ∩ M
7
M ′ ← C∆M
8
Imprimir M ′
~ +
e)
9
Gerar grafo D(
+
10
EliminarArestasDesnecessarias(D( e ))
11
EnumEmpPerfeitosRecursivo (D( e), M )
12
Gerar grafo D( e)
13
EliminarArestasDesnecessarias(D( e ))
14
15
+
−
−
−
EnumEmpPerfeitosRecursivo (D( e), M ′ )
fim
em M ′ . No próximo passo, o algoritmo gera dois subproblemas de mesma natureza:
enumerar todos os emparelhamentos perfeitos que possuem e, e todos os emparelhamentos perfeitos que não possuem o arco e. Vamos analisar primeiramente o
segundo caso: para enumerar os emparelhamentos perfeitos que não contém e, con~ e em seguida o
~ −
e) que é obtido removendo-se o arco e de D,
sideramos o digrafo D(
−
Algoritmo 10 chama-se a si mesmo, passando como parâmetro o digrafo D( e) e o emparelhamento perfeito M ′ . Já no primeiro caso, para enumerar os emparelhamentos
+
~
perfeitos que possuem e, consideramos o grafo D( e) que é obtido removendo-se de D
as extremidades de e, e todos os arcos que partem ou chegam nelas. Note que todo
+
emparelhamento perfeito de D( e) corresponde a um único emparelhamento perfeito
~ que contém e. Portanto, para se enumerar os emparelhamentos perfeitos que
de D
contém e, o Algoritmo 10 executa uma chamada recursiva, tendo como parâmetros
+
+
D( e) e M . Note que um emparelhamento perfeito de D( e) não conterá o arco e,
Capítulo 4. Emparelhamentos em grafos bipartidos
32
Algoritmo 11: EliminarArestasDesnecessarias
~
Entrada: D
1 início
~ para todo (u, v) ∈ A(D)
~
2
cf c ← ComponentesFortementeConexas (D)
faça
3
se cf c(u) 6= cf c(v) então
~ ← A(D)
~ \ (u, v)
4
A(D)
5
fim se
6
fim para todo
7 fim
porém e estará presente em M (que foi passado como parâmetro na chamada recursiva). Portanto, todo emparelhamento perfeito obtido pela diferença simétrica de
+
M com um circuito dirigido de D( e) é um emparelhamento perfeito do grafo G que
contém e.
4.3.3
Análise de complexidade
Nesta seção, vamos analisar a complexidade de tempo para enumerar todos os emparelhamentos perfeitos de um grafo bipartido.
Primeiramente, vamos analisar a complexidade do Algoritmo 3, que encontra
um emparelhamento máximo em um grafo bipartido G = (V1 ∪ V2 , E). Sejam n =
|V1 ∪ V2 | e m = E. Cada execução das linhas 8 a 11 corresponde a um busca em
profundidade no grafo, o que leva tempo O(n + m). Para se inicializar o vetor
pai, gasta-se tempo O(n). Já o Algoritmo 5, no pior caso, levará tempo O(n),
pois um caminho terá, no máximo, n vértices. Temos, no máximo, |V2 | chamadas
ao Algoritmo 5, pois no pior caso todos os caminhos a serem invertidos possuirão
apenas uma aresta {a ∈ V1 \ S, b ∈ V2 \ S}. Cada iteração no laço das linhas 4
a 17 levará, no pior caso, tempo O(n2 + n + |V2 |) (um grafo bipartido terá, no
máximo, n2 arestas). Teremos, no máximo, n/2 iterações no laço das linhas 4 a 17,
pois inicialmente S pode ser vazio, e no pior caso, apenas 2 vértices são inseridos
33
4.3. Enumerando os emparelhamentos perfeitos
em S a cada iteração (linha 15). Portanto, o Algoritmo 3 demandará um tempo
O(n/2(n2 + n + |V2 |)) = O(n3 ).
No Algoritmo 10, as operações de eliminar arestas desnecessárias e gerar os digra+
−
fos D( e) e D( e) levam tempo O(n). Portanto, o tempo de execução do Algoritmo 10
é proporcional a O(n3 + nk), onde k é o número de emparelhamentos perfeitos. Há
√
um algoritmo mais rápido, que demanda tempo O = ( n(n + m)) [14], porém não
utilizamos devido a complexidade de implementação e também porque ele não melhoraria muito a velocidade de execução na prática do algoritmo para o Problema
do Isomorﬁsmo de Grafos proposto nesta dissertação.
CAPÍTULO
5
Algoritmo para o Problema do Isomorfismo de Grafos
Neste capítulo será apresentado o algoritmo que desenvolvemos para o Problema
do Isomorﬁsmo de Grafos, baseado em um processo de simulação sobre os vértices
de um grafo G. O objetivo destas simulações é encontrar partições do conjunto de
vértices de G, que servirão de base para decidir se dois grafos G e H são isomorfos.
O algoritmo é dividido em três partes principais: a primeira consiste em executar
p-simulações em G e H, aplicando-se uma função f sobre seus respectivos conjuntos
de vértices. Ao ﬁnal desta etapa, os vértices estarão agrupados em classes, e os
vértices de uma determinada classe compartilham as mesmas propriedades entre si
(grau, padrão de vizinhança).
Na segunda etapa, construímos um grafo bipartido R = (V (G) ∪ V (H), E), onde
o conjunto de arestas representa a compatibilidade entre os vértices de G e H. Esse
grafo R é construído de acordo com o particionamento de V (G) e V (H) obtidos na
etapa anterior.
Capítulo 5. Algoritmo para o Problema do Isomorﬁsmo de Grafos
36
A terceira etapa consiste em encontrar emparelhamentos perfeitos de R e veriﬁcar
se um emparelhamento perfeito M corresponde a um isomorﬁsmo ϕ(V (G)) → V (H).
5.1
Simulação
Como deﬁnimos na Seção 2.1.2, o conjunto NG (v) é também chamado de vizinhança
aberta de um vértice v no grafo G. Agora vamos deﬁnir NG [v] = NG (v) ∪ {v} como
a vizinhança fechada 1 de v em G.
Um multiconjunto é deﬁnido como um par (X, m), onde X é um conjunto qualquer e m : X → N∗ uma função que associa cada elemento de X a um inteiro positivo.
Denotamos por M a família de todos os multiconjuntos ﬁnitos de N.
Fixamos um grafo G = (V, E), uma função f : M → N e um inteiro positivo k.
Para um vértice p ∈ V , que será denominado pivô, uma p-simulação é uma sequência
de vetores x(1) , x(2) , . . . , x(k) com entradas em N indexados por V que são deﬁnidos
(1)
indutivamente pela seguinte relação. Para i = 1, atribua xv
= 1 se v = p ou
(1)
xv = 0 se v 6= p. Para i > 1, deﬁna
(i−1)
x(i)
: w ∈ NG [v]} .
v = f {xw
Por conveniência, suponha que x(0) é um vetor nulo.
Exemplo
A Figura 5.1 traz o exemplo de uma p-simulação no grafo da Figura 5.2, para k = 8,
com a função f dada por
f (M ) =
X
m.
m∈M
1
Suprimiremos o subscrito quando o grafo estiver subentendido no texto.
37
5.1. Simulação
x(0)
x(1)
0
1
0
p
0
x(2)
0
1
0
p
0
0
0
1
0
0
0
0
0
0
0
0
0
x(3)
0
0
7
2
p
2
25
9
p
2
9
28
10
6
0
26
2
x(6)
10
0
x(7)
81
105
92
1031
370
370
1359
p
1359
350
48
1288
198
92
794
1274
348
12
2
x(8)
291
p
105
p
46
26
2
2
0
28
p
6
0
0
x(5)
x(4)
3
1
p
186
60
732
258
Figura 5.1: Simulação em um grafo G
5.1.1
Efeitos de uma p-simulação
(i)
Sabemos que, na i-ésima rodada de uma p-simulação, xv é o valor atribuído pela
função f ao vértice v. Antes do inicio da p-simulação, todos os vértices possuem
valor 0, não sendo possível distinguir os vértices entre si. Na primeira rodada, temos
que o valor de p é 1 e o valor dos demais vértices é 0. Com isso, podemos dizer que
a primeira rodada de uma p-simulação distingue o vértice pivô dos demais vértices
do grafo. Conforme o número de rodadas vai aumentando, mais vértices podem ser
Capítulo 5. Algoritmo para o Problema do Isomorﬁsmo de Grafos
38
distinguidos uns dos outros através dos valores atribuídos pela função f . Assim, se
(i)
(i)
na i-ésima rodada os valores de u e v forem diferentes (isto é, se xu 6= xv ), dizemos
que u é distinguível de v, e estes vértices permanecem distinguíveis até o ﬁnal da
simulação (mesmo que em alguma rodada posterior eles voltem a ter o mesmo valor).
Desse modo, podemos associar uma partição dos vértices do grafo a cada rodada
de uma p-simulação, onde vértices são agrupados de acordo com seus respectivos
valores naquela rodada. Antes de formalizar o conceito de uma partição associada
a uma rodada vamos deﬁnir partição e alguns conceitos relacionados.
5.1.2
Partições
Uma partição de V é uma família de subconjuntos disjuntos não vazios de V , onde
a união de todos eles é o próprio conjunto V . Uma partição ordenada de V é uma
sequência (V1 , V2 , . . . , Vr ) tal que {V1 , V2 , . . . , Vr } é uma partição de V . O conjunto
de todas as partições de V e o conjunto de todas as partições ordenadas de V são
′
denotados por P(V ) e P (V ), respectivamente.
′
Seja π ∈ P(V ) ∪ P (V ) uma partição (ordenada ou não). Cada membro de π
é chamado de célula. Dizemos que uma célula em π é trivial se tiver apenas um
elemento. Se todas as células de π forem triviais, então π é chamada de partição
discreta, enquanto que, se π possuir apenas uma célula, então π é chamada de
partição unitária.
Duas partições ordenadas (V1 , V2 , . . . , Vr ) e (W1 , W2 , . . . , Ws ) são compatíveis se
r = s e, para todo índice i entre 1 e r, vale que |Vi | = |Wi |.
Seja π = (V1 , V2 , . . . , Vr ) uma partição ordenada de V . Para cada x ∈ V deﬁnimos idx(x, π) = i, onde x ∈ Vi .
Sejam π1 e π2 duas partições. Dizemos que π1 é um refinamento de π2 se toda
célula de π1 for um subconjunto de alguma célula de π2 . Dizemos que (W1 , . . . , Ws )
é um refinamento ordenado de (V1 , . . . , Vr ) se:
39
5.1. Simulação
(i) {W1 , . . . , Ws } for um reﬁnamento de {V1 , . . . , Vr };
(ii) se Wi ⊆ Va , Wj ⊆ Vb e a < b, então i < j.
5.1.3
Partição associada a uma rodada
(i)
Vamos deﬁnir agora, para cada i ∈ {0, 1, . . . , k}, uma partição ordenada ψG,p que
será a partição associada a x(i) , ou seja, a partição associada à i-ésima rodada de
(i)
uma p-simulação. Em ψG,p , temos que u está na mesma célula que v se e somente
se
(j)
x(j)
u = xv ,
(5.1)
(i)
para todo j, com 1 ≤ j ≤ i. Para deﬁnir a ordem das células em ψG,p , sejam u e v
vértices em células distintas, e seja j, com 1 ≤ j ≤ i, o primeiro índice que viola a
(i)
condição (5.1). Nesse caso, a célula de u precede a célula de v em ψG,p se e somente
(j)
(j)
(i)
se xu < xv . Observe que, para todo i ∈ [k], ψG,p é um reﬁnamento ordenado de
(i−1)
ψG,p .
Proposição 1. Se a função f satisfaz f ({0, . . . , 0}) = 0 e f ({1, 0, 0, . . . , 0}) 6= 0
(2)
então a partição ψG,p possui exatamente três células, a saber:
(2)
ψG,p = NḠ (p), NG (p), {p} .
(1)
Demonstração. Pela deﬁnição de simulação, temos que ψG,p terá apenas o vértice p
distinguido dos demais, porque o vetor x(1) possuirá o valor 0 em todas as posições,
(1)
exceto em xp , que terá o valor 1.
Seja Miv um multiconjunto formado pelos valores do vetor x(i) nas posições
dadas pelos vértices de NG [v], para v ∈ V (G). Na segunda rodada, o vetor x(2) terá
a seguinte conﬁguração: a posição p terá o valor 1, pois em x(1) , todas as posições
(1)
relativas aos vizinhos de p possuem valor 0, e xp possui valor 1. Logo, M1p terá um
Capítulo 5. Algoritmo para o Problema do Isomorﬁsmo de Grafos
40
único elemento 1, e os demais serão 0. Com isso, f (M1p ) 6= 0 por hipótese.
Agora vamos analisar a aplicação da função nos vizinhos de p. Para todo u ∈
NG (p), o multiconjunto M1u também será formado por um único elemento 1, e
os demais 0. Isso ocorre pois o único vizinho de u que possui o valor 1 em sua
respectiva posição no vetor x(1) é p. Os demais terão o valor 0 em suas posições em
x(1) . Também por hipótese, f (M1u ) 6= 0.
Para todo o vértice w ∈ NḠ (p), o multiconjunto M1w conterá apenas elementos
0, pois todas as posições relativas aos vértices da vizinhança fechada de w possui o
valor 0 em x(1) . Portanto, f (M1w ) = 0 por hipótese.
(2)
Com isso, o vetor x(2) apresentará a seguinte conﬁguração: xp
(2)
= 1, xu = 1,
(2)
(2)
para todo u ∈ NG (p), e xw = 0, para todo w ∈ NḠ (p). Note que, apesar de xp
(2)
e xu poderem possuir os mesmos valores, o vértice p já foi distinguido na primeira
(2)
(2)
rodada. Com isso, a partição ψG,p possuirá três células: ψG,p [1] contendo os vértices
(2)
(2)
que não são vizinhos de p, ψG,p [2], com os vértices vizinhos de p e ψG,p [3] contendo
apenas o vértice p, o que encerra a prova.
5.1.4
Algoritmo para uma p-simulação
Antes de apresentarmos o algoritmo para uma p-simulação, é necessário algumas
deﬁnições: dada a partição ordenada π, denotamos por π[i] a i-ésima célula de π. O
símbolo · denota a operação de concatenação de duas partições, que é deﬁnida por:
π · σ = (π[1], π[2], . . . , π[r], σ[1], σ[2], . . . , σ[s]), onde r = |π| e s = |σ|. Sejam π e σ
duas partições compatíveis. Dizemos que duas células π[i] e σ[j] são correspondentes
se i = j. Seja X uma célula de uma partição, denotamos por Xhji o j-ésimo menor
elemento de X. O Algoritmo 12 formaliza os passos envolvidos em uma p-simulação2 .
(k)
O Algoritmo 13 subdivide uma célula Z, da partição ψG,p de acordo com os
2
O conceito de partição igualitária será abordado na Seção 5.3
41
5.1. Simulação
Algoritmo 12: Simulação
Entrada: G, p, f : M → N
(k)
Saída: Célula ψG,p
1 início
2
k←1
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
(1)
ψG,p ← V (G) \ {p} · {p}
para todo v ∈ V (G) faça
(1)
xv ← 0
fim para todo
(1)
xp ← 1
repita
ψ̃ ← ()
(k)
t ← |ψG,p |
para todo v ∈ V (G) faça
(k)
(k−1)
xv ← f {xw
: w ∈ NG [v]}
fim para todo
para i de 1 até t faça
(k)
ψ̃ ← ψ̃· ReﬁnaCelula(ψG,p [i], x(k) )
fim para
(k)
ψG,p ← ψ̃
k ←k+1
(k)
até ψG,p seja igualitária;
(k)
retorna ψG,p
fim
valores obtidos através da aplicação de uma função f em NG (z), para todo z ∈ Z.
Estes valores são armazenados no vetor x(k) , na posição z. O primeiro passo é
ordenar os vértices de Z de acordo com os valores que eles possuem no vetor x(k) ,
de modo crescente. Este passo é realizado para otimizar o processo de veriﬁcação
de quais vértices possuem valores iguais no vetor x(k) (pela equação 5.1 dois vértices
(k)
a, b estão em uma mesma célula se e somente se xa
(k)
= xb ). O próximo passo
do algoritmo é realizar uma varredura no vetor x(k) , inserindo os vértices em suas
(k)
respectivas células. Uma nova célula é criada sempre que o valor de xs for diferente
(k)
de seu antecessor xs−1 .
Capítulo 5. Algoritmo para o Problema do Isomorﬁsmo de Grafos
42
Algoritmo 13: ReﬁnaCelula
1
2
3
4
5
6
7
8
9
10
11
12
13
Entrada: Célula Z, vetor x(k)
Saída: Partição π
início
(k)
Ordenar Z conforme o valor de xz para cada z ∈ Z, em ordem crescente
j←1
π[1] ← {Zh1i}
para s de 2 até |Z| faça
(k)
(k)
se xZ<s−1> 6= xZhsi então
j ← j +1
π[j] ← ∅
fim se
π[j] ← π[j] ∪ {Zhsi}
fim para
retorna π
fim
5.1.5
Árvore de partição
Uma árvore de partição TG,p é construída a partir das partições de V associadas
a cada rodada de uma p-simulação em G. O conjunto de nós dessa árvore é a
(i)
união disjunta de todas as partições ψG,p , para i ∈ {0, 1, . . . , k}. A raiz de TG,p é
(0)
(i)
o conjunto V (que é uma célula da partição ψG,p ) e um nó A ∈ ψG,p é ﬁlho de um
(i−1)
nó C ∈ ψG,p
se A ⊆ C. Ademais, se dois nós A e B no nível i são ﬁlhos de um
(i)
(i)
mesmo nó C, então A encontra-se à esquerda de B se xa < xb para algum a ∈ A e
(i)
(i)
algum b ∈ B; e A encontra-se à direita de B se xa > xb para algum a ∈ A e algum
b ∈ B. Isto ocorre pois no reﬁnamento de uma célula, os vértices são ordenados de
forma crescente (linha 2 do Algoritmo 13). Por ﬁm, temos que a partição associada
(k)
à última rodada da p-simulação será denotada por ψG,p , ou seja, ψG,p = ψG,p .
Exemplo
A Figura 5.3 traz a árvore de partição para a p-simulação mostrada na Figura 5.1.
A Figura 5.2 abaixo mostra o grafo de exemplo com seus vértices rotulados.
43
5.1. Simulação
a
p
g
b
f
e
c
d
Figura 5.2: Grafo G rotulado
(0)
ψG,p
Partição Unitária
{a, b, c, d, e, f, g}
ψG,p
{a, g}
{p}
ψG,p
{b, f }
{a, g}
{p}
ψG,p
{b, c, d, e, f }
{c, d, e}
(1)
{p}
(2)
(3)
(4)
{d}
{c, e}
{b, f }
{a, g}
{p}
ψG,p
{d}
{c, e}
{b, f }
{a, g}
{p}
ψG,p
{b, f }
{a, g}
{p}
ψG,p
(5)
(6)
{d}
{e}
{c}
{d}
{e}
{c}
{f }
{b}
{a, g}
{p}
ψG,p
{d}
{e}
{c}
{f }
{b}
{a, g}
{p}
ψG,p
Figura 5.3: Árvore de partição.
(7)
(8)
Capítulo 5. Algoritmo para o Problema do Isomorﬁsmo de Grafos
5.2
44
Propriedades de uma p-simulação
Lema 1. Seja ϕ um isomorfismo entre grafos G e H, e seja v ∈ V (G) um vértice
qualquer. Então NH [ϕ(v)] = ϕ(NG [v]).
Demonstração. Seja v como no enunciado e w ∈ NG (v) um vértice qualquer. Se
{v, w} ∈ E(G), então {ϕ(v), ϕ(w)} ∈ E(H). Portanto ϕ(w) ∈ NH (ϕ(v)). Como w
é qualquer, ﬁca estabelecido que NH (ϕ(v)) ⊇ ϕ(NG (v)).
Reciprocamente, seja u ∈ NH (ϕ(v)) um vértice qualquer. Como ϕ é sobrejetora,
existe w ∈ V (G) com ϕ(w) = u. Com isso temos
{ϕ(w), ϕ(v)} ∈ E(H) ⇒ {v, w} ∈ E(G) ⇒ w ∈ NG (v).
Conclui-se que u = ϕ(w) ∈ ϕ(NG (v)). Como u é qualquer, ﬁca estabalecida a
inclusão NH (ϕ(v)) ⊆ ϕ(NG (v)).
Para concluir a prova do lema, observe que ϕ(v) ∈ NH [ϕ(v)] ∩ ϕ(NG [v]).
A seguir, apresentamos a propriedade fundamental de uma p-simulação.
Teorema 2. Sejam G ∼
= H dois grafos, seja ϕ um isomorfismo entre G e H, e
seja ψG,p = (V1 , . . . , Vr ) a partição associada a uma p-simulação em G, para algum
p ∈ V (G). Nessas condições, vale que
ψH,ϕ(p) = (ϕ(V1 ), . . . , ϕ(Vr )),
(5.2)
onde ϕ(Vi ) = {ϕ(v) : v ∈ Vi }.
Demonstração. Sejam G, H, ϕ e p conforme o enunciado do teorema. Seja q = ϕ(p).
Seja x(1) , . . . , x(k) uma p-simulação em G, e seja y (1) , . . . , y (k) uma q-simulação em
45
5.2. Propriedades de uma p-simulação
H. Vamos primeiro mostrar, por indução em i, que
(i)
∀ v ∈ V (G) : yϕ(v) = x(i)
v .
(5.3)
(1)
(1)
Quando i = 1, pela deﬁnição de p-simulação, temos xv = 1 se v = p e xv = 0
(1)
se v 6= p. Pela deﬁnição de q-simulação, temos yϕ(v) = 1 se ϕ(v) = q (isto é, se
(1)
v = p) e xϕ(v) = 0 caso contrário. Assim, segue que (5.3) vale para i = 1.
Suponha então que i > 1, e suponha que (5.3) valha com i − 1 no lugar de i.
Nesse caso, temos
(i)
yϕ(v) = f {yu(i−1) : u ∈ NH [ϕ(v)]}
(i−1)
= f {yϕ(w) : w ∈ ϕ−1 (NH [ϕ(v)]}
(i−1)
= f {yϕ(w) : w ∈ ϕ−1 (ϕ(NG [v]))}
(i−1)
= f {yϕ(w) : w ∈ NG [v]}
= f {x(i−1)
: w ∈ NG [v]}
w
= x(i)
v .
(i)
A primeira igualdade segue da deﬁnição de yϕ(v) , a segunda do fato de que ϕ é
um isomorﬁsmo, a terceira segue do Lema 1, a quinta segue da hipótese de indução
(i)
e a sexta da deﬁnição de xv . Portanto (5.3) é verdade.
Agora temos que mostrar (5.2). Sejam u, v ∈ V (G) vértices quaisquer. Se
(j)
(j)
u, v ∈ Vℓ para algum ℓ, então xu = xv para todo j ∈ {0, 1, . . . , k}. Usando (5.3),
(j)
(j)
temos que yϕ(u) = yϕ(v) para todo j ∈ {0, 1, . . . , k}, o que implica que ϕ(u) e ϕ(v)
pertencem à mesma célula de ψH,ϕ(p) . Isso mostra que {ϕ(V1 ), . . . , ϕ(Vr )} é um reﬁnamento de ψH,ϕ(p) . Um argumento simétrico mostra que ψH,ϕ(p) é um reﬁnamento
de {ϕ(V1 ), . . . , ϕ(Vr )}. Portanto, as células dessas partições são as mesmas.
Por se tratar de uma identidade de partições ordenadas, resta ainda mostrar
Capítulo 5. Algoritmo para o Problema do Isomorﬁsmo de Grafos
46
que a ordem relativa das células de ψH,ϕ(p) e (ϕ(V1 ), . . . , ϕ(Vr )) é a mesma. Para
(ℓ)
(ℓ)
isso, suponha que u ∈ Vi e v ∈ Vj com i < j. Isso implica que xu < xv
(m)
algum ℓ ≤ k e xu
(m)
= xv
para
para todo m entre 0 e ℓ − 1. Mas então, por (5.3),
(m)
(m)
(ℓ)
(ℓ)
vale que ∀m ∈ {0, . . . , ℓ − 1} temos yϕ(u) = yϕ(v) e yϕ(u) < yϕ(u) . Isso implica que
idx(ϕ(u), ψH,ϕ(p) ) < idx(ϕ(v), ψH,ϕ(p) ) e portanto a ordem das classes também é
respeitada.
O Teorema 2 permite que p-simulações sejam usadas para resolver o Problema
do Isomorﬁsmo de Grafos, pois a célula em que um dado vértice é colocado, ao ﬁnal
de uma p-simulação, independe do nome inicialmente dado a ele. É por esse motivo
que, se dois grafos G e H são isomorfos e se q ∈ V (H) é a imagem de um vértice
p ∈ V (G) por algum isomorﬁsmo em Iso(G, H), então uma p-simulação em G e uma
q-simulação em H fazem a mesma classiﬁcação dos vértices. Essa idéia é resumida
no enunciado a seguir.
Corolário 1. A partição ψG,p independe dos nomes dos vértices do grafo.
5.3
Algoritmo proposto
Denotamos por L(G) o conjunto
L(G) = {ψG,p : p ∈ V (G)}.
Nesta seção, propomos o Algoritmo 14, que decide se dois grafos G e H são
isomorfos. Vamos supor que V (G) ∩ V (H) = ∅.
Este algoritmo tem como entrada os grafos G e H, e como saída sim se os grafos
são isomorfos, e não caso contrário. Podemos dividir o algoritmo em duas etapas
principais: na primeira, fazemos p-simulações para todo vértice p ∈ V (G) e, ao ﬁnal
47
5.3. Algoritmo proposto
Algoritmo 14: Veriﬁca se dois grafos são isomorfos
Entrada: Grafos G e H
Saída: sim se G e H são isomorfos, não caso contrário
1 início
2
π←∅
3
para todo p ∈ V (G) faça
4
ψG,p ← Simulação(G, p, f )
5
se ψG,p é discreta então
6
π ← ψG,p
7
Sai do laço
8
senão
9
L(G) ← L(G) ∪ {ψG,p }
10
11
12
13
14
15
16
17
18
se π =
6 ∅ então
{u1 }, {u2 }, . . . , {un } ← π
para todo q ∈ V (H) faça
fazer q-simulação em H para obter ψH,q
se ψH,q é discreta então
{v1 }, {v2 }, . . . , {vn } ← ψH,q
ϕ ← mapeamento que leva ui 7→ vi
se ϕ é um isomorfismo de G em H então
retorna sim
retorna não
19
20
21
22
23
24
25
26
27
senão
para todo q ∈ V (H) faça
fazer q-simulação em H para obter ψH,q
L(H) ← L(H) ∪ {ψH,q }
Construir grafo bipartido R = (V (G) ∪˙ V (H), E = ∅)
para todo {p, q} ∈ E(R) faça
se ψG,p for compatível com ψH,q então
E(R) ← E(R) ∪ {p, q}
M ← Emparelhamento perfeito obrido pelo Algoritmo 3
~ ← D(R,
~
D
M)
~ M)
EnumerarCandidatoIsomorﬁsmo(D,
retorna não
28
29
30
31
32
fim
desta etapa, temos o conjunto L(G) que contém todas as partições ψG,p . A segunda
etapa do algoritmo é a veriﬁcação do isomorﬁsmo. Esta etapa subdivide-se em dois
Capítulo 5. Algoritmo para o Problema do Isomorﬁsmo de Grafos
48
casos:
1. existe vértice u ∈ V (G) tal que ψG,u é a partição discreta;
2. ψG,u não é discreta para nenhum vértice u.
No primeiro caso, é necessário fazer q-simulações para todo vértice q ∈ V (H) e
veriﬁcar, para toda partição ψH,q que for discreta, se o mapeamento que leva ψG,u nos
vértices correspondentes de ψH,q (preservando a ordem das células) é um isomorﬁsmo
entre G e H. Se algum desses mapas for um isomorﬁsmo, o algoritmo para e devolve
sim. Caso contrário o algoritmo devolve não.
No segundo caso, considera-se um grafo bipartido R = (V (G)∪V (H), E), inicialmente vazio (sem nenhuma aresta entre V (G) e V (H)). Para cada par não ordenado
{p, q} de V (G) × V (G), acrescenta-se a aresta {p, q} se as partições ψG,p e ψH,q são
compatíveis3 . Caso contrário, não pode haver um isomorﬁsmo que mapeie p ∈ V (G)
a q ∈ V (H). Portanto, neste caso, a aresta {p, q} não é inserida em R.
Dados v ∈ V e W ⊂ V , deﬁnimos dG (v, W ) como o número de elementos de W
′
que são adjacentes a v em G. Dizemos que π ∈ P(V ) ∪ P (V ) é uma partição
igualitária com relação ao grafo G (ou G-igualitária) se, para todo par de células
V1 , V2 ∈ π (não necessariamente distintas) e para quaisquer elementos x, y ∈ V1 ,
temos que dG (x, V2 ) = dG (y, V2 ). O Teorema 3 mostra que, se uma partição Gigualitária for encontrada, então a árvore de partições estabilizará.
A Figura 5.4 mostra um exemplo de partição G-igualitária e não igualitária:
na partição π, tomamos as célula V1 = {0, 1} e V2 = {2, 3}. A partição π não é
igualitária, pois dG (0, V2 ) = 0 e dG (1, V2 ) = 1.
3
Como visto anteriormente, duas partições são compatíveis se ambas possuírem o mesmo número
de células, e se todas as células correspondentes possuírem o mesmo número de elementos
49
5.3. Algoritmo proposto
π não é igualitária.
σ é igualitária.
0
0
1
5
1
5
6
6
2
4
2
4
3
3
Figura 5.4: Exemplos de partições.
Teorema 3. Uma árvore de partições Tp se estabiliza ao encontrar uma partição
G-igualitária.
(k)
Demonstração. Seja π a partição ψG,p e i = idx(v, π) para todo v ∈ V (G). Deﬁnimos
por dyj o grau que um vértice qualquer da célula π[y] possui dentro da célula π[j].
(k)
Observe que d(v, π[j]) = dij . Deﬁnimos por xi
(k+1)
Pela deﬁnição de xv
(k)
o valor de xu para algum u ∈ π[i].
temos:
= f {x(k)
x(k+1)
v
u : u ∈ N [v]}
(k)
= f {xidx(u,π) : u ∈ N [v]}
=f
[
n
j=1
(k)
dij {xj }
Observe que a fórmula à direita do símbolo = independe de v, mas apenas de
(k+1)
i = idx(v, π), que é igual para todo vértice em π[i]. Portanto, xv
todo v ∈ π[i].
(k)
(k)
(k+1)
é igual para
(k)
Logo, se ψG,p é G-igualitária, então ψG,p [j] = ψG,p [j],∀j ∈ {0, . . . , |ψG,p |}.
Capítulo 5. Algoritmo para o Problema do Isomorﬁsmo de Grafos
5.3.1
50
Emparelhamentos perfeitos e isomorfismo
Após a construção do grafo bipartido R, o algoritmo veriﬁca se os emparelhamentos
perfeitos de R podem corresponder a um isomorﬁsmo. Como vimos na Seção 4.1, o
algoritmo de Uno [38] lista todos os emparelhamentos perfeitos em um grafo bipartido de forma recursiva, onde em um ramo da recursão é ﬁxada uma aresta arbitrária
e em um emparelhamento, e no outro ramo e é retirado do emparelhamento perfeito.
Como o objetivo do nosso algoritmo é encontrar um isomorﬁsmo entre os grafos G
e H, ao escolher uma aresta e, podemos ignorar os emparelhamentos perfeitos que
não correspondem a um isomorﬁsmo. Para tanto, modiﬁcamos o Algoritmo 10 de
modo que arestas cujas extremidades estão em células não correspondentes não se~ +
e).
jam inseridas em D(
Veja o exemplo: dados dois grafos G e H, um isomorﬁsmo ϕ : V (G) → V (H) e
as arestas a = {p, q}, f = {u, v} ∈ R. Suponha que ϕ(p) = q. Se ϕ(u) ∈ ψH,q [i] e
v ∈ ψH,q [j], com i 6= j, então ϕ 6= v. Portanto, a aresta f não estará presente no
~ +
e) pois não há um isomorﬁsmo que leva u em v.
digrafo D(
D
+
−
D(e1 )
+ +
+ −
D(e1 e2 )
+ + +
D(e1 e2 e3 )
D(e1 )
− +
D(e1 e2 )
+ + −
D(e1 e2 e3 )
+ − +
D(e1 e2 e3 )
− −
D(e1 e2 )
+ − −
D(e1 e2 e3 )
− + +
D(e1 e2 e3 )
D(e1 e2 )
− + −
D(e1 e2 e3 )
− − +
D(e1 e2 e3 )
− − −
D(e1 e2 e3 )
Figura 5.5: Exemplo de árvore de recursão do Algoritmo 15.
Assim, reescrevemos o Algoritmo 10 de modo que as arestas de R cujas extremidades estejam em células não correspondentes em duas partições compatíveis ψG,p
~ +
e).
e ψH,q não estejam presentes no digrafo D(
Na primeira chamada do Algoritmo 15 é passado o digrafo D(R, M ), onde M foi
+
obtido pelo Algoritmo 3. O grafo D( e) é obtido eliminando-se as pontas da aresta
51
5.3. Algoritmo proposto
−
e e todas as arestas não correspondentes. Já o grafo D( e) é obtido deletando-se a
aresta e.
Algoritmo 15: EnumerarCandidatoIsomorﬁsmo
Entrada: D, M
1 início
2
se M ′ corresponde a um isomorfismo então
3
para e imprime isomorﬁsmo entre G e H
4
fim se
5
se E(D) = ∅ então
6
Fim
7
fim se
8
Encontrar um circuito C M -alternante
9
Escolher uma aresta arbitrária e ∈ C ∩ M
10
M ′ ← C∆M
+
11
Gerar grafo D( e)
12
EliminarArestasDesnecessarias (D( e))
13
EnumerarCandidatoIsomorﬁsmo (D( e), M )
14
Gerar grafo D( e)
15
EliminarArestasDesnecessarias (D( e))
16
17
+
+
−
−
−
EnumerarCandidatoIsomorﬁsmo (R( e), M ′ )
fim
+
Como visto na Seção 4.1, todo emparelhamento perfeito obtido em D( e) pode
ser estendido a R adicionando-se a aresta e. Já o emparelhamento perfeito obtido
−
através de D( e) é também um emparelhamento perfeito de R.
CAPÍTULO
6
Algoritmo Pratical Graph Isomorphism
Neste Capítulo descreveremos o funcionamento do algoritmo utilizado no programa
Nauty, proposto por McKay [25].
O algoritmo Pratical Graph Isomorphism (PGI) é baseado em uma rotulação
canônica e no grupo de automorﬁsmos de um grafo. Uma rotulação canônica pode
ser entendida como um processo que recebe um grafo e devolve uma rotulação dos
vértices desse grafo, sempre produzindo a mesma saída quando as entradas são grafos
isomorfos. A ideia central do PGI é comparar as rotulações canônicas de G e H e
caso sejam iguais, os grafos G e H são isomorfos. Caso contrário, o PGI retorna
não-isomorfos.
Para encontrar uma rotulação canônica, o PGI se divide em duas partes principais: o procedimento de reﬁnamento e o procedimento de busca. Em linhas gerais,
o procedimento de reﬁnamento tem como entrada uma partição qualquer π e como
retorno uma partição igualitária dos vértices de G que é um reﬁnamento de π. O pro-
Capítulo 6. Algoritmo Pratical Graph Isomorphism
54
cedimento de busca é um algoritmo recursivo que recebe uma partição G-igualitária
e introduz uma assimetria nesta partição para uma subsequente execução do procedimento de reﬁnamento. Este processo recursivo é repetido até se encontrar todas1
as partições discretas de V (G). A cada partição discreta obtida pelo procedimento
de busca é associado um grafo, e a rotulação será um destes grafos, escolhido segundo
uma ordem pré-estabelecida.
Nas próximas seções, mostraremos o funcionamento da etapa de reﬁnamento e
do algoritmo recursivo do procedimento de busca.
6.1
Rotulação canônica e isomorfo canônico
Nesta seção, deﬁniremos o conceito de isomorfo canônico. Para tanto, precisamos
introduzir alguns conceitos iniciais: seja G o conjunto de todos os grafos sobre o
conjunto de vértices {1, . . . , n}. Uma rotulação canônica é uma função C : G → G tal
que, para todo par de grafos isomorfos G e H pertencentes a G, vale C(G) = C(H).
Para um dado grafo G, o grafo C(G) é chamado isomorfo canônico.
Seja π uma partição discreta de V = {1, 2, . . . , n}. Deﬁnimos γπ ∈ Sn como
uma permutação tal que γπ (v) = idx(v, π). Denotamos por γπ (G) o grafo obtido
através da permutação γπ em V (G). Seja P = {x1 , y1 }, . . . , {xt , yt } o conjunto
de pares
V
2 .
Podemos representar o grafo G por um vetor característico χE(G) , de
comprimento t = n(n − 1)/2, que possui o valor 1 na posição j se o par {xj , yj } ∈
E(G) e 0 caso contrário. Dados grafos G e H, deﬁnimos G H se χE(G) ≤ χE(H)
lexicograﬁcamente.
Para encontrar um isomorfo canônico, o PGI reﬁna uma partição dos vértices de
G, de modo a encontrar uma partição discreta de V (G). Caso isso não seja possível,
o PGI constrói uma árvore de busca na qual todas as folhas corresponderão a uma
1
Este processo não lista todas as n! partições discretas, mas apenas aquelas que terão utilidade
para se encontrar a rotulação canônica.
55
6.2. Reﬁnamento de partições
partição discreta π de V (G). O isomorfo canônico C(G) então será o maior grafo
γπ (G), de acordo com a ordem de , onde π é uma partição discreta associada a uma
folha da árvore de partições de G. Em seguida, o PGI executa os mesmos passos
para calcular C(H) e veriﬁca o isomorﬁsmo entre G e H comparando os isomorfos
canônicos C(G) e C(H), pois G e H serão isomorfos se e somente se C(G) = C(H).
A comparação dos isomorfos canônicos é muito eﬁciente, pois basta comparar o
conjunto de arestas destes grafos, que demanda um tempo O(n2 ).
Na próxima seção, mostraremos como o PGI executa o procedimento de reﬁnamento.
6.2
Refinamento de partições
O objetivo principal da etapa de reﬁnamento é encontrar uma partição G-igualitária
que seja um reﬁnamento de uma determinada partição π. A seguir, mostraremos
como este procedimento é realizado.
Para uma partição ordenada π de V (G), existe um conjunto Z(π) de partições
ordenadas de V (G) que são reﬁnamentos de π e, ao mesmo tempo, partições Gigualitárias.2 Note que Z(π) 6= ∅, pois a partição discreta é sempre G-igualitária e é
um reﬁnamento de π. É possível argumentar3 que existe uma partição ζ(π) ∈ Z(π)
que satisfaz σ ≤ ζ(π) para toda σ ∈ Z(π). Em outras palavras, existe uma única
partição que é um reﬁnamento G-igualitário de π com o número mínimo possível de
células, denominada ζ(π).
A estratégia do PGI é encontrar a partição ζ(π) a partir de uma partição ordenada π. Mas para determinados tipos de grafos (por exemplo, os grafos vérticetransitivos), a partição ζ(π) não será discreta. Isso torna-se uma diﬁculdade para
o PGI, pois como vimos, o isomorfo canônico está associado a uma partição dis2
3
Neste capítulo, omitiremos as provas. Para detalhes, consulte o artigo [25]
Seção 2.3 de [25]
Capítulo 6. Algoritmo Pratical Graph Isomorphism
56
creta de V (G). Para resolver este problema, o PGI cria novas partições ordenadas
σ1 , σ2 , . . . , σm (onde m é o tamanho da maior célula de ζ(π)), reﬁna cada uma destas
novas partições ordenadas obtidas e executa este processo sucessivamente até encontrar partições discretas de V (G) (esta etapa será explicada nas Seções 6.4 e 6.5). A
seguir, apresentamos o algoritmo que executa o procedimento de reﬁnamento para
uma partição ordenada π.
6.3
Algoritmo de refinamento
O objetivo principal do Algoritmo 16 é encontrar uma partição G-igualitária que seja
um reﬁnamento da partição π passada como argumento. Para tanto, o Algoritmo
16 de reﬁnamento recebe, além do grafo G, uma partição ordenada π ∈ V (G) e uma
sequência α = (W1 , W2 , . . . , WM ) de células distintas de π, que respeita a ordem de
π, e tem como saída uma partição ordenada, denominada R(G, π, α), de V (G). O
processo de reﬁnamento consiste, a grosso modo, em veriﬁcar o número de vizinhos
que os vértices de uma célula de π possuem em relação a algum elemento de α.
Esta veriﬁcação será abordada mais adiante, ainda nesta seção. Dado que antes da
execução do Algoritmo 16, a única partição de V (G) conhecida é a partição unitária
π = V (G), então, inicialmente, o Algoritmo 16 receberá como argumentos o grafo
G, a partição unitária π e a sequência de células α = π. Pelo Teorema 4, temos que
a partição R(G, π, π) retornada pelo Algoritmo 16 é a partição ζ(π).
Teorema 4. ([25]) Para todo grafo G e toda partição ordenada π de V (G), vale que
R(G, π, π) = ζ(π).
Antes de mostrarmos o Algoritmo 16, faz-se necessário algumas deﬁnições: o
tamanho de uma partição ordenada π é a quantidade de células que ela possui,
57
6.3. Algoritmo de reﬁnamento
denotado por |π|. Lembre-se de que π[i] denota a i-ésima célula de π. Denotamos por π[i, j] a sequência de células (π[i], π[i + 1], . . . , π[j]). O símbolo · denota a operação de concatenação de duas partições, que é deﬁnida por: π · σ =
(π[1], π[2], . . . , π[r], σ[1], σ[2], . . . , σ[s]), onde r = |π| e s = |σ|. Seja γ uma permutação do conjunto V (G). A imagem de v ∈ V sob γ é denotada por γ(v). Para
W ⊆ V , temos γ(W ) = {γ(w)|w ∈ W }. Para π = (V1 , V2 , · · · , Vr ), deﬁnimos
γ(π) = (γ(V1 ), γ(V2 ), · · · , γ(Vr )).
A sequência de células α pode ser entendida como uma fila de processamento
de células. Para cada m, a célula π[k] é subdividida. Esta subdivisão é feita com
base no número de vizinhos que cada vértice em π[k] possui no conjunto α[m]. Ao
término desta subdivisão, a célula π[k] foi quebrada em novas células (σ[1], . . . , σ[s]).
Dados os subconjuntos X, Y ⊂ V (G), dizemos que X é homogêneo em relação a Y
se d(x, Y ) = d(x′ , Y ) para todo x, x′ ∈ X. Pelo modo como π[k] foi subdividida, os
vértices x, y ∈ σ[i] têm o mesmo número de vizinhos dentro de α[m]. Portanto, todo
σ[i] é homogêneo em relação à α[m].
Após a subdivisão, todo σ[i] é inserido na ﬁla. Isso é necessário pois para uma
célula π[j] qualquer, π[j] poderia ser homogênea em relação a π[k]. Com o reﬁnamento, π[j] pode não ser homogênea em relação a todas as células de σ criadas a
partir de π[k]. Portanto, é necessário incluir todo4 σ[i] em α. Por ﬁm, π̃ é atualizado, concatenando-se π̃ com σ. Em outras palavras, a célula π[k] é substituída por
σ, visto que σ é um reﬁnamento de π[k]. O processo então se repete com a próxima
célula da lista de processamento, até que o algoritmo encontre uma partição discreta,
ou termine de processar todas as células da lista α.
Caso a partição retornada não seja discreta, é necessário então continuar o processo para forçar a obtenção de uma partição que seja discreta. Isto é feito através
4
No Algoritmo 16, a maior célula de σ (linha 23: σ[t]) não é inserida na fila devido a uma
otimização do algoritmo.
Capítulo 6. Algoritmo Pratical Graph Isomorphism
58
Algoritmo 16: Procedimento de Reﬁnamento
Entrada: Grafo G, partição ordenada π de V (G) e α subsequência de π
Saída: R(G, π, α)
1 início
2
π̃ ← π
3
m←1
4
enquanto π̃ não é discreta ou m ≤ |α| faça
5
π̂ ← ()
6
para k de 1 até |π̃| faça
7
p ← |π̃[k]|
8
(u1 , . . . , up ) ← elementos de π̃[k] ordenados de tal forma que
d(ui , α[m]) < d(uj , α[m]) ⇒ i < j
9
σ ← ({u1 })
10
s←1
11
para i de 2 até p faça
12
se d(ui−1 , W ) = d(ui , W ) então
13
σ[s] ← σ[s] ∪ {ui }
14
senão
15
s←s+1
16
σ[s] ← {ui }
17
fim se
18
fim para
19
se s > 1 então
20
t ← arg max{|σ[t]| : 1 ≤ t ≤ s}
21
se α[j] = π̃[k] para algum j (m ≤ j ≤ |α|) então
22
α[j] ← σ[t]
23
fim se
24
α ← α · σ[1, t − 1] · σ[t + 1, s]
25
π̂ ← π̂ · σ
26
fim se
27
fim para
28
π̃ ← π̂
29
m←m+1
30
fim enquanto
31
retorna π̃
32 fim
de um algoritmo recursivo, que isola um vértice na partição obtida e executa o
procedimento de reﬁnamento novamente. Nas duas próximas seções, mostraremos
como é feita a escolha deste vértice e explicaremos o funcionamento deste algoritmo
59
6.4. Partições aninhadas
recursivo.
6.4
Partições aninhadas
Seja π = (V1 , V2 , . . . , Vk ) uma partição ordenada de V (G) e v ∈ Vi para algum i.
Deﬁnimos π ◦ v =
1. π, se |Vi | = 1.
2. (V1 , . . . , Vi−1 , v, Vi \ v, Vi+1 , . . . , Vk ), se |V1 | > 1
Deﬁnimos também π ⊥ v = R(G, π ◦ v, (v)).
Teorema 5. ([25]) Seja G um grafo, π uma partição ordenada de V (G) e suponha
que há alguma partição G-igualitária σ tal que π ≤ σ. Se escolhermos α ⊆ π tal que
para todo W ∈ σ, temos X ⊆ W para, no máximo, um X ∈ π \ α, então, R(G, π, α)
é G-igualitária.
Pelo Teorema 5, temos que R(G, π ◦ v, (v)) é G-igualitária.
Dado um grafo G, uma partição ordenada π de V (G) e uma sequência v =
v1 , v2 , . . . , vm−1 de vértices distintos de V , deﬁnimos por ν = (π1 , π2 , . . . , πm ) a
sequência de partições aninhadas derivadas de G, π e v, onde:
1. π1 = R(G, π, π) e,
2. πi = πi−1 ⊥ vi−1 , para 2 ≤ i ≤ m.
O conjunto de todas as sequências de partições aninhadas derivadas de algum
G, π e um vetor v de elementos distintos de V é denotado por N (V ).
6.5
Árvore de busca
Uma árvore de busca T (G) é o conjuntos de todas as partições aninhadas ν ∈ N (V )
tal que ν é derivado de um grafo G, uma partição ordenada π de V (G) e uma
Capítulo 6. Algoritmo Pratical Graph Isomorphism
60
sequência v1 , v2 , . . . , vm−1 onde, para 1 ≤ i ≤ m − 1, vi é um elemento da primeira
célula não trivial de πi que possui o menor tamanho. A deﬁnição implica que |πi | <
|πi+1 | para 1 ≤ i < m. A sequência ν também é chamada de nó da árvore. Seja
ν = (π1 , π2 , . . . , πm ) um nó da árvore T (G). Dizemos que ν é um nó terminal se
πm for discreta. Dados dois nós ν1 = (π1 , π2 , . . . , πm ) e µ = (π1 , π2 , . . . , πm , πm+1 ),
dizemos que µ é sucessor (ou filho) de ν. De mesmo modo, dizemos que ν é antecessor
(ou pai) de µ. O nó ν = (π1 ) é um ancestral comum a todos os nós, já que a escolha
de π1 está ﬁxada: π1 = R(G, π, π).
O algoritmo 17 encontra todos os nós da árvore T (G), tendo como partição inicial
a partição unitária π = ({V (G)}).
Algoritmo 17: Árvore de Busca
Entrada: Grafo G
1 início
2
π ← V (G)
3
ν ← R(G, π, π)
4
Gera(ν)
5 fim
Observe que o Algoritmo 18 é um algoritmo de backtracking, onde os nós ν de
T (G) são gerados de forma recursiva5 . Note que, no Algoritmo 18, a partição π será
impressa se ela for discreta. As demais partições do nó ν são utilizadas apenas para
o backtracking do algoritmo, pois como já visto anteriormente, apenas as partições
discretas geradas neste processo terão utilidade para o cômputo do isomorfo canônico
C(G) e, consequentemente, para a veriﬁcação do isomorﬁsmo.
Observe que não serão todas as n! partições discretas de V (G) que serão geradas
pelo Algoritmo 18. Isso ocorre pois os vértices que serão isolados durante o backtrac5
O algoritmo 17 é uma versão recursiva do algoritmo iterativo apresentado por B. McKay em
[25], página 55.
61
6.5. Árvore de busca
Algoritmo 18: Gera(ν)
Entrada: ν
1 início
2
k ← |ν|
3
π ← ν[k]
4
se π é discreta então
5
Imprime π
6
retorna
7
fim se
8
t ← min{i : |π[i]| > 1}
9
W ← π[t]
10
para cada v ∈ W faça
11
σ←π⊥v
12
Gera(ν · (σ))
13
fim para
14 fim
king estarão obrigatoriamente em uma célula não trivial (veja linha 7 do Algoritmo
18). Assim, células triviais não serão alteradas e terão suas posições ﬁxadas no nós
descendentes na árvore de busca.
Além disso, pelo Teorema 6, temos que a quantidade de partições discretas geradas pelo Algoritmo 18 para o grafo G é igual ao número de partições discretas
geradas pelo Algoritmo 18 para o grafo H.
Figuras 6.1 e 6.2 temos um exemplo de um grafo G e a árvore de busca T (G).
1
0
2
3
4
5
6
Figura 6.1: Grafo G.
7
Capítulo 6. Algoritmo Pratical Graph Isomorphism
62
π = ({0, . . . , 7})
π1 = ({7}, {6}, {0}, {5}, {1, 2}, {4}, {3})
ν1 = π1 , π2 = ({7}, {6}, {0}, {5}, {1}, {2}, {4}, {3})
ν2 = π1 , π2 = ({7}, {6}, {0}, {5}, {2}, {1}, {4}, {3})
Figura 6.2: Árvore T (G).
Como visto anteriormente, para cada partição discreta π impressa pelo Algoritmo 18, associamos uma permutação γπ . Ao aplicarmos esta permutação no grafo
G, obtemos o grafo γπ (G), que é representado por seu vetor característico χ
.
E γπ (G)
Denotamos por P (G) o conjunto de todos grafos γπ (G). Assim, deﬁnimos o isomorfo
canônico de G como sendo o grafo
C(G) = max{γπ (G) ∈ P (G)}
Teorema 6. ([25]) Se G e H são isomorfos, então P (G) = P (H).
Como visto, o Algoritmo 18 produz as partições discretas que serão utilizadas
para o cômputo do isomorfo canônico, através da associação de uma partição discreta
a uma permutação do grafo G. O processo então se repete para o grafo H e comparase os isomorfos canônicos C(G) e C(H). O Teorema 6 nos garante que se os grafos
G e H são isomorfos, então C(G) = C(H), pois como P (G) = P (H), então o grafo
máximo de P (G) é o mesmo para P (H).
A veriﬁcação do isomorfo canônico pode ser otimizada, utilizando-se o grupo de
automorﬁsmos para descartar partições discretas impressas pelo Algoritmo 18. Na
próxima seção, veremos como o PGI utiliza o grupo de automorﬁsmos de G para
podar a árvore de busca T (G) e otimizar ainda mais a busca pelo isomorfo canônico.
63
6.6. Podando a árvore de busca
6.6
Podando a árvore de busca
Se o grupo de automorﬁsmos de um grafo G for grande (isso ocorre, por exemplo,
em grafos vértice-transitivos), então a árvore de busca T (G) terá muitos ramos
e, consequentemente, o número de nós terminais será, no mínimo, o tamanho de
Aut(G). Como a árvore é explorada em profundidade, então os automorﬁsmos que
são descobertos durante a busca serão usados para podar a árvore de busca.
Sejam ν1 e ν2 dois nós terminais de uma árvore de busca T (G), e sejam π ∈
ν1 e σ ∈ ν2 partições discretas. Suponha que ν1 está a esquerda (será analisado
primeiramente pelo Algoritmo 18) de ν2 na árvore de busca. Se γπ (G) = γσ (G),
então a permutação τ : V → V deﬁnida por τ (v) = γπ−1 γσ (v) é um automorﬁsmo
de G.
Seja γ uma permutação de Sn e σ uma partição ordenada de V (G). Denotamos
por γ(σ) a partição ordenada obtida permutando-se os vértices de σ conforme γ. Seja
ν = (π1 , π2 , . . . , πm ) um nó na árvore T (G). Denotamos por γ(ν) a permutação γ
aplicada a todas as partições de ν, ou seja, γ(ν) = (γ(π1 ), γ(π2 ), . . . , γ(πm )). Sejam
a, b, c nós de T (G) tal que a é o ancestral comum mais recente de ν1 e ν2 , b é o ﬁlho
de a e ancestral de ν1 e c é o ﬁlho de a e ancestral de ν2 . A permutação τ envia π a σ,
ﬁxa a e envia b para c. Em outras palavras, temos que τ (π) = τ (σ) e τ (b) = τ (c).
Denotamos por T (G, x) uma subárvore de T (G) enraizada pelo nó x. Então T (G, c) é
isomorfa a T (G, b) (pela permutação τ ), e portanto o conjunto de grafos gerados por
nós terminais de T (G, c) é o mesmo conjunto de grafos gerados por nós terminais de
T (G, b). Como a árvore de busca T (G) é explorada em profundidade, então T (G, b)
é visitada antes de T (G, c). Portanto6 , não é necessário explorar T (G, c) e a busca
continua pelo nó a.
6
O Algoritmo 18 não incorpora esta otimização
CAPÍTULO
7
Resultados
Neste capítulo vamos discutir os resultados obtidos nos testes do Algoritmo PGI e
também do algoritmo proposto. Para realizar os testes, implementamos o Algoritmo
proposto na linguagem C++, e o programa Nauty foi obtido no sítio nauty and
Traces [24] e testados em um computador com processador Intel Core i5 2.5GHz,
4GB de memória RAM e sistema operacional OS X Mavericks. Para efetuar os
testes, utilizamos um gerador de pares de grafos isomorfos e também bibliotecas
de grafos disponíveis em [23]. Nas próximas seções, o programa Nauty refere-se a
implementação do algoritmo PGI, e o programa Mabi (Matching based isomorphism
é a implementação do algoritmo proposto nesta dissertação, ambos na linguagem
C++, utilizando o compilador gcc, com diretiva de compilação O2. O código fonte
da implementação do algoritmo proposto está disponível no Anexo 9 e no repositório
Bitbucket 1 .
1
https://bitbucket.org/rodrigedilson/dissertacao-isomorfismo-grafos
Capítulo 7. Resultados
7.1
66
Gerador de grafos aleatórios - instâncias positivas
Utilizamos o modelo de Erdős-Rényi, que gera um grafo G com n vértices e com m
arestas, em média. A probabilidade de uma aresta {u, v} ser inserida no grafo G é
dada por
p=
m
n .
2
Para se gerar o grafo G, para cada par de vértices {u, v} é realizado um sorteio,
com probabilidade p de sucesso. Caso o sorteio seja bem sucedido, a aresta {u, v}
é inserida em G. O número de arestas do grafo será, com alta probabilidade, muito
próximo a m, pois a distribuição do número de arestas é binominal e possui grande
concentração em torno da média2 .
Já o grafo H, isomorfo a G, é gerado permutando-se os vértices de G com uma
permutação γ ∈ Sn aleatória.
7.1.1
Resultados
A metodologia de testes foi gerar cinco pares de grafos com n vértices e m arestas e
executar tanto o programa Nauty quanto o programa Mabi para cada par de grafo.
Nas Tabelas 7.1 e 7.2, os valores se referem à média dos tempos de execução, em
segundos. Para os grafos densos, a quantidade de arestas foi dada por
grafos esparsos, a quantidade de arestas foi deﬁnida por 2n.
Tabela 7.1: Grafos aleatórios densos.
Vértices
50
100
200
400
2
Veja desigualdade de Chernoff, em [1].
Nauty
0.004
0.017
0.150
0.945
Mabi
0.287
2.490
22.876
191.211
n
2
e para os
67
7.1. Gerador de grafos aleatórios - instâncias positivas
Tabela 7.2: Grafos aleatórios esparsos.
Vértices
50
100
200
400
Nauty
0.002
0.002
0.002
0.005
Mabi
0.257
0.375
3.877
24.014
Como observado nas tabelas, o algoritmo PGI teve um desempenho muito superior em todos os testes realizados. O motivo principal para tal superioridade é que
o PGI isola um vérice a cada chamada recursiva do algoritmo de reﬁnamento. Em
outras palavras, a cada chamada recursiva, o algoritmo de reﬁnamento tem como
parâmetro uma partição obtida em uma etapa anterior do backtracking. Já o algoritmo proposto, por não ser um algoritmo de backtracking, não se utiliza da partição
obtida em uma simulação como informação para realizar uma próxima simulação.
Além disso o PGI possui uma otimização, que é a poda de ramos da árvore,
diminuindo a quantidade de grafos permutados que são obtidos a partir de uma
partição discreta de V (G), e consequentemente haverá uma diminuição do tempo de
cômputo do isomorfo canônico.
Ademais, na etapa de reﬁnamento do PGI, a partição obtida sempre será igualitária, o que não ocorre no algoritmo proposto, uma vez que o processo de simulação
pode se estabilizar sem encontrar uma partição igualitária. Isto ocorre pois a função
f utilizada na simulação não é bijetora, e ao implementarmos uma versão do Mabi
com uma função bijetora, o desempenho se mostrou ainda pior, pois era necessário
armazenar na memória todos os multiconjuntos encontrados durante as simulações.
Capítulo 7. Resultados
7.2
68
Grafos com alto padrão de simetria
McKay, ao testar o Algoritmo PGI, mencionou em seu artigo alguns tipos de grafos
que trariam diﬁculdades para o PGI resolver o Problema de Isomorﬁsmo de Grafos.
Dentre eles, testamos os grafos fortemente regulares.
É possível demonstrar formalmente que o Mabi é ineﬁciente para grafos fortemente regulares. Um grafo regular G, com v vértices e grau k, é dito fortemente
regular se houver inteiros i e j tal que todo par de vértices adjacentes possua i
vizinhos em comum e todo par de vértices não adjacentes possua j vizinhos em
comum.3
Para efetuar os testes com grafos fortemente regulares, aplicamos uma permutação aleatória a um grafo obtido na biblioteca de grafos fortemente regulares, e assim
conseguimos um par de grafos fortemente regulares isomorfos. Como no caso dos
grafos aleatórios, executamos os programas Nauty e Mabi por cinco vezes e calculamos a sua média. A seguir, a Tabela 7.3 apresenta os resultados obtidos para grafos
fortemente conexos isomorfos (tempo em segundos):
Tabela 7.3: Grafos fortemente regulares isomorfos.
Características
v = 25, k = 12, i = 5, j = 6
v = 36, k = 14, i = 4, j = 6
7.2.1
Nauty
0.002
0.002
Mabi
0.041
16.496
Grafos fortemente regulares não isomorfos
Ao testarmos um par de grafos fortemente regulares não isomorfos com as mesmas características (v, k, i e j comum aos dois grafos), detectamos que o processo
de simulação gerava v partições igualitárias com apenas três células, e todas elas
3
Para os testes, utilizamos a biblioteca de grafos fortemente regulares, disponível em [23].
69
7.2. Grafos com alto padrão de simetria
compatíveis entre si. Com isso, o grafo bipartido R tornava-se completo, com v!
emparelhamentos perfeitos (lembre-se que uma aresta {p, q} é inserida em R se e
somente se as partições ψG,p e ψH,q são compatíveis), e consequentemente o algoritmo proposto um número exponencial de testes para veriﬁcar que G e H não eram
isomorfos, o que deixou o programa Mabi ineﬁciente.
É possível demonstrar formalmente que o algoritmo proposto é ineﬁciente para
(2)
grafos fortemente regulares. Seja G um grafo fortemente regular e π = ψG,p uma
partição obtida a partir de uma p-simulação. Pela Proposição 1, π possui apenas
três células e podemos argumentar que π é G-regular. A célula π[3] contém apenas
o vértice p, a célula π[2] possui os vizinhos de p e a célula π[1] contém os vértices
não adjacentes a p. A homegeneidade de π[3] com relação às outras duas células é
óbvia. Cada vértice u ∈ π[2] possui um vizinho em π[3], e pela deﬁnição de grafo
fortemente regular, u e p possuem i vizinhos em comum. Como todos os vizinhos
de p estão em π[2], logo u terá i vizinhos em π[2]. Também pela deﬁnição, cada
vértice v ∈ π[1] possui j vizinhos em π[2], pois v e p não são adjacentes, e portanto
possuem j vizinhos em comum. Como os vizinhos de p estão em π[2], cada vértice
v terá j vizinhos em π[2]. Como G é k-regular, então todo vértice u ∈ π[2] terá
k − i − 1 vizinhos em π[1] e todo v ∈ π[1] terá k − j vizinhos em π[1]. Portanto π é
G-igualitária, para todo p ∈ V (G). Pelo Teorema 3, a p-simulação se estabiliza ao
encontrar uma partição igualitária. Ao construir o grafo R, ele será completo, pois
todo par de partições ψG,p e ψG,q será compatível, o que torna o algoritmo proposto
ineﬁciente para grafos fortemente regulares.
A Figura 7.1 ilustra o particionamento obtido após a realização de um p-simulação
em um grafo fortemente regular. Os valores marcados nas setas representam a quantidade de vizinhos que um vértice presente em uma célula possui em relação a uma
outra célula.
Capítulo 7. Resultados
70
0
k−i−1
k
π[3]
π
j
1
π[2]
π[1]
i
k−j
Figura 7.1: Partição π obtida após uma simulação em um grafo fortemente regular.
A seguir, temos a Tabela 7.4 que mostra os resultados obtidos para pares de
grafos fortemente conexos não isomorfos, mas que possuem os mesmos valores de
v, k, i, j em ambos.
Tabela 7.4: Grafos fortemente regulares não isomorfos.
Características
v = 25k = 12i = 5j = 6
v = 36k = 14i = 4j = 6
Nauty
0.001
0.004
Mabi
28.334
4929.180
CAPÍTULO
8
Considerações Finais
Neste trabalho apresentamos conceitos básicos sobre teoria dos grafos, estudamos
o Problema do Isomorﬁsmo de Grafos e o algoritmo proposto por McKay. Como
contribuição, apresentamos um algoritmo para o caso geral do PIG e um estudo
detalhado do algoritmo PGI.
Como visto no capítulo anterior, apesar de o algoritmo proposto não ter superado o algoritmo PGI em desempenho, houve uma contribuição válida, pois não
foi encontrado na literatura um algoritmo para o PIG baseado em emparelhamentos perfeitos em grafo bipartido. Além disso, acreditamos que este algoritmo seja
de fácil paralelização, o que traria um ganho de desempenho. Na próxima seção,
apresentamos quais serão os trabalhos futuros relacionados a esta dissertação.
Capítulo 8. Considerações Finais
8.1
72
Trabalhos futuros
Em um trabalho futuro, pretendemos paralelizar este algoritmo, utilizando a seguinte
estratégia: em primeiro lugar, a simulação seria paralelizada, pois foi veriﬁcado
empiricamente que este processo demanda muito tempo de processamento. Em
segundo momento, a paralelização seria na geração de emparelhamentos perfeitos.
Outro trabalho a ser desenvolvido é paralelizar o algoritmo PGI.
Além disso, pretendemos implementar duas melhorias no algoritmo proposto,
com o objetivo de diminuir o tempo de execução: a primeira é modiﬁcar o processo de
simulação, para que uma simulação tenha como parâmetro, além do vértice pivô e a
função f , uma partição obtida em uma simulação anterior. A segunda melhoria é na
etapa de veriﬁcação do isomorﬁsmo a partir de um emparelhamento perfeito. Se um
emparelhamento perfeito M não corresponde a um isomorﬁsmo ϕ, certamente haverá
um par de arestas e = {i, j} e a = {u, v} de M em que i = ϕ(j) e u 6= ϕ(v). Com
isso, podemos modiﬁcar o algoritmo que gera os emparelhamentos perfeitos, de modo
que as arestas e e a não estejam simultaneamente nos próximos emparelhamentos
perfeitos gerados.
Outras pesquisas a serem desenvolvidas é comparar o consumo de memória dos
dois algoritmos, e testá-los em sistemas com pouca memória RAM e cache inexistente
ou limitado.
Bibliografia
[1] Alon, N. e Spencer, J. (2004). The Probabilistic Method. Wiley-Interscience
series in discrete mathematics e optimization. Wiley.
[2] Arvind, V. e Torán, J. (2005). Isomorphism testing: Perspective e open problems.
Bulletin of the EATCS, 86:66–84.
[3] Babai, L., Grigoryev, D. Y., e Mount, D. M. (1982). Isomorphism of graphs
with bounded eigenvalue multiplicity. In Proceedings of the fourteenth annual
ACM symposium on Theory of computing, STOC ’82, pages 310–324, New York,
NY, USA. ACM.
[4] Babai, L. e Luks, E. M. (1983). Canonical labeling of graphs. In Proceedings
of the Fifteenth Annual ACM Symposium on Theory of Computing, STOC ’83,
pages 171–183, New York, NY, USA. ACM.
[5] Barbosa, R. M. (1975). Combinatória e Grafos. Nobel.
[6] Chen, W.-K. (1997). Graph theory e its engineering applications. Advanced
Series in Electrical e Computer Engineering. World Scientiﬁc.
Bibliograﬁa
[7] Colbourn, C. J. (1981).
74
On testing isomorphism of permutation graphs.
Networks, 11(1):13–21.
[8] Conte, D., Foggia, P., Sansone, C., e Vento, M. (2004). Thirty Years Of Graph
Matching In Pattern Recognition. International Journal of Pattern Recognition e
Artificial Intelligence.
[9] Farouk, R. M. (2011). Iris recognition based on elastic graph matching e gabor
wavelets. Computer Vision e Image Understanding, 115(8):1239–1244.
[10] Foggia, P., Sansone, C., e Vento, M. (2001). A performance comparison of ﬁve
algorithms for graph isomorphism. Proc. of the 3rd IAPR TC-15 Workshop on
Graph-based Representations in Pattern Recognition, pages 188–199.
[11] Foggia, P., Sansone, C., e Vento, M. (2004). A (sub)graph isomorphism algorithm for matching large graphs. IEEETPAMI: IEEE Transactions on Pattern
Analysis e Machine Intelligence, 26.
[12] Gallian, J. (1994). Contemporary abstract algebra. D.C. Heath.
[13] Goldreich, O., Micali, S., e Wigderson, A. (1986). Proofs that yield nothing but
their validity e a methodology of cryptographic protocol design. In Proceedings
of the 27th Annual Symposium on Foundations of Computer Science, SFCS ’86,
pages 174–187, Washington, DC, USA. IEEE Computer Society.
[14] Hopcroft, J. e Karp, R. (1973). An n5/2 algorithm for maximum matchings in
bipartite graphs. SIAM Journal on Computing, 2(4):225–231.
[15] Hopcroft, J. E. e Wong, J. K. (1974). Linear time algorithm for isomorphism
of planar graphs (preliminary report). In Proceedings of the sixth annual ACM
symposium on Theory of computing, STOC ’74, pages 172–184, New York, NY,
USA. ACM.
75
Bibliograﬁa
[16] Jenner, B., Köbler, J., McKenzie, P., e Torán, J. (2003). Completeness results
for graph isomorphism. J. Comput. Syst. Sci., 66(3):549–566.
[17] Jukna, S. (2001). Extremal Combinatorics: With Applications in Computer
Science. Springer.
[18] Köbler, J., Schöning, U., e Torán, J. (1993). The Graph Isomorphism Problem:
Its Structural Complexity. Progress in Theoretical Computer Science. Birkhäuser.
[19] Leiserson, C., Cormen, T., Rivest, R., e Stein, C. (2002). Algoritmos: teoria e
prática. Campus.
[20] Lueker, G. S. e Booth, K. S. (1979). A linear time algorithm for deciding
interval graph isomorphism. J. ACM, 26(2):183–195.
[21] Luks, E. M. (1982). Isomorphism of graphs of bounded valence can be tested
in polynomial time. Journal of Computer e System Sciences, 25(1):42 – 65.
[22] Martin, D. M. (2011). Teoria dos grafos: notas de aula. Online.
[23] McKay, B. (2013). Combinatorial data. [Online; http://cs.anu.edu.au/ bdm/data/graphs.html; accessado em 28-Dezembro-2013].
[24] McKay,
B.
e
Piperno,
A.
(2013).
nauty
e
traces.
[Online;
http://cs.anu.edu.au/ bdm/nauty/; accessado em 28-Dezembro-2013].
[25] McKay, B. D. (1981). Practical graph isomorphism. In Congressus Numerantium (10th. Manitoba Conference on Numerical Mathematics e Computing),
volume 30, pages 45–87.
[26] Miller, G. (1980). Isomorphism testing for graphs of bounded genus. In Proceedings of the twelfth annual ACM symposium on Theory of computing, STOC
’80, pages 225–235, New York, NY, USA. ACM.
Bibliograﬁa
76
[27] Nandi, R. C. (2006). Isomorﬁsmo de grafos aplicado à comparação de impressões
digitais. Mestrado, UFPR.
[28] Netto, P. O. B. (2006). Grafos: Teoria, modelos, algoritmos. Edgard Blucher,
4 edition.
[29] Pedarsani, P. e Grossglauser, M. (2011).
On the privacy of anonymized
networks. In Proceedings of the 17th ACM SIGKDD international conference
on Knowledge discovery e data mining, KDD ’11, pages 1235–1243, New York,
NY, USA. ACM.
[30] Raymond, J. W. e Willett, P. (2002). Maximum common subgraph isomorphism
algorithms for the matching of chemical structures. Journal of Computer-Aided
Molecular Design, 16(7):521–533.
[31] Rodrigues,
P. M. (2013).
Emparelhamentos em grafos.
[Online;
http://www.math.ist.utl.pt/ pmartins/EMF/Notas/Grafos5.pdf; accessado em
28-Dezembro-2013].
[32] Schmidt e Druﬀel (1976). A fast backtracking algorithm to test directed graphs
for isomorphism using distance matrices. JACM: Journal of the ACM, 23.
[33] Sipser, M. (1996). Introduction to the Theory of Computation. International
Thomson Publishing, 1st edition.
[34] Szwarcﬁter, J. L. (1988). Grafos e algoritmos computacionais. Campus, Rio de
Janeiro.
[35] Torán, J. (2004). On the hardness of graph isomorphism. SIAM J. Comput.,
33(5):1093–1108.
[36] Ullmann, J. R. (1976a). An algorithm for subgraph isomorphism. JACM:
Journal of the ACM, 23.
77
Bibliograﬁa
[37] Ullmann, J. R. (1976b). An algorithm for subgraph isomorphism. J. ACM,
23(1):31–42.
[38] Uno, T. (2001). A fast algorithm for enumerating bipartite perfect matchings.
In ISAAC, pages 367–379.
CAPÍTULO
9
Anexo
1
#pragma once
2
#i f n d e f CELULA_H_
3
#d e f i n e CELULA_H_
4
5
#i n c l u d e <s e t >
6
7
u s i n g namespace s t d ;
8
9
10
c l a s s Cell {
public :
11
Cell () ;
12
Cell ( int label ) ;
13
14
s e t <i n t > v e r t i c e s ;
15
16
17
int label ;
79
b o o l o p e r a t o r <( C e l l c ) {
18
return label < c . label ;
19
}
20
21
};
22
23
#e n d i f /∗ CELULA_H_ ∗/
codigo/cell.h
1
2
#i f n d e f CELULA_CPP_
3
#d e f i n e CELULA_CPP_
4
5
#i n c l u d e " c e l l . h "
6
7
Cell : : Cell () {
8
label = 0;
9
}
10
11
Cell : : Cell ( int label ) {
t h i s −>l a b e l = l a b e l ;
12
13
}
14
15
#e n d i f
codigo/cell.cpp
1
#pragma once
2
#i f n d e f GRAPH_H_
3
#d e f i n e GRAPH_H_
4
5
#i n c l u d e < l i s t >
6
#i n c l u d e <i o s t r e a m >
7
#i n c l u d e <f s t r e a m >
Capítulo 9. Anexo
80
8
9
u s i n g namespace s t d ;
10
11
// Uma c l a s s e para r e p r e s e n t a r g r a f o s d i r i g i d o s
12
c l a s s Digraph {
13
protected :
14
int n ;
// numero de v e r t i c e s
15
i n t m;
// numero de a r e s t a s
16
17
// Matriz de a d j a c e n c i a
18
i n t ∗∗ matrix ;
19
20
// Uma m a t r i z de a d j a c e n c i a e s p e c i a l
21
/∗
/
22
∗
|
Adj [ u ] . end ( )
|
the i t e r a t o r pointing to v in u ’ s l i s t
i f v i s not i n u ’ s a d j a c e n c y
list ,
23
∗ M[ u ] [ v ] = <
24
∗
otherwise .
25
∗
26
∗/
27
\
l i s t <i n t > : : i t e r a t o r ∗∗M;
28
29
30
public :
l i s t <i n t > ∗ a d j ;
31
32
Digraph
( int n) ;
33
Digraph
( Digraph ∗G) ;
// C o n s t r u t o r
// C o n s t r u t o r ( f a z c o p i a de G)
34
35
/∗ C o n s t r o i um g r a f o d i r i g i d o a p a r t i r do g r a f o b i p a r t i d o balan−
36
∗ ceado R e emparelhamento M. As a r e s t a s de M sÃ£o o r i e n t a d a s de
37
∗ ’ b a i x o ’ para ’ cima ’ e a s a r e s t a s de R \ M sÃ£o o r i e n t a d a s de
38
∗ ’ cima ’ para ’ b a i x o ’ .
81
39
∗/
~ Digraph ( ) ;
// D e s t r u t o r
42
bool insert_arc ( in t u , in t v) ;
// I n s e r e o a r c o ( u , v )
43
b o o l remove_arc ( i n t u , i n t v ) ;
// Remove o a r c o ( u , v )
44
bool exists_arc ( in t u , in t v) ;
// V e r i f i c a s e ( u , v ) e s t a
40
41
presente
45
bool invert_arc ( in t u , in t v) ;
// Troca orientaÃ§Ã£o do a r c o (
u , v)
46
bool invert_path ( i n t u , const i n t ∗ parent ) ;
47
48
l i s t <i n t > : : i t e r a t o r r e m o v e _ a r c _ a l t e r n a t i v e ( i n t u , i n t v ) ;
//
Remove o a r c o ( u , v )
49
50
l i s t <i n t > : : i t e r a t o r a r c ( i n t u , i n t v ) ;
51
52
void p r i n t ( ) ;
53
v o i d read_graph
// Imprime o g r a f o na t e l a
( FILE ∗ ) ;
// Le um g r a f o nÃ£o d i r i g i d o de
um a r q u i v o
54
v o i d read_digraph ( FILE ∗ ) ;
// Le um g r a f o d i r i g i d o de um
arquivo
55
56
i n t get_n ( ) ;
// R etorna a q u a n t i d a d e de v e r t i c e s
57
i n t get_m ( ) ;
// R etorna a q u a n t i d a d e de a r e s t a s
58
59
60
// Transpoe o g r a f o ( i n p l a c e )
61
void t r an sp ose ( ) ;
62
63
// R etorna uma c o p i a do g r a f o t r a n s p o s t o
64
Digraph ∗ g e t _ t r a n s p o s e ( ) ;
65
66
// R etorna a m a t r i z de a d j a c e n c i a s
Capítulo 9. Anexo
c o n s t i n t ∗∗ adjacency_ma tri x ( ) ;
67
68
82
};
69
70
#e n d i f
codigo/digraph.h
1
#i f n d e f GRAFOS_CPP_
2
#d e f i n e GRAFOS_CPP_
3
4
#i n c l u d e " d i g r a p h . h "
5
#i n c l u d e <i o s t r e a m >
6
#i n c l u d e <f s t r e a m >
7
8
Digraph : : Digraph ( i n t n ) {
t h i s −>n = n ;
9
10
a d j = new l i s t <i n t > [ n ] ;
11
matrix = NULL;
12
// I n i c i a l i z a a m a t r i z de a d j a c e n c i a
13
M = new l i s t <i n t > : : i t e r a t o r ∗ [ n ] ;
14
f o r ( i n t i = 0 ; i < n ; i ++) {
15
M[ i ] = new l i s t <i n t > : : i t e r a t o r [ n ] ;
16
f o r ( i n t j = 0 ; j < n ; j ++)
17
M[ i ] [ j ] = a d j [ i ] . end ( ) ;
18
}
19
20
}
21
22
23
Digraph : : Digraph ( Digraph ∗G) {
n = G−>n ;
24
25
a d j = new l i s t <i n t > [ n ] ;
26
matrix = NULL;
27
83
// Aloca a m a t r i z de a d j a c e n c i a e i n i c i a l i z a com " 0 "
28
M = new l i s t <i n t > : : i t e r a t o r ∗ [ n ] ;
29
f o r ( i n t i = 0 ; i < n ; i ++) {
30
M[ i ] = new l i s t <i n t > : : i t e r a t o r [ n ] ;
31
f o r ( i n t j = 0 ; j < n ; j ++)
32
M[ i ] [ j ] = a d j [ i ] . end ( ) ;
33
}
34
35
36
// Copia o s a r c o s
37
f o r ( i n t i = 0 ; i < n ; i ++)
f o r ( l i s t <i n t > : : i t e r a t o r j = G−>a d j [ i ] . b e g i n ( ) ; j != G−>a d j [ i ] .
38
end ( ) ; j ++) {
a d j [ i ] . push_front ( ∗ j ) ;
39
M[ i ] [ ∗ j ] = a d j [ i ] . b e g i n ( ) ;
40
}
41
42
// Mantem a m a t r i z a t u a l i z a d a
}
43
44
v o i d Digraph : : t r a n s p o s e ( ) {
45
l i s t <i n t > ∗ oldAdj = a d j ;
46
a d j = new l i s t <i n t > [ n ] ;
47
48
49
f o r ( i n t i = 0 ; i < n ; i ++)
f o r ( i n t j = 0 ; j < n ; j ++)
M[ i ] [ j ] = a d j [ i ] . end ( ) ;
50
51
52
53
f o r ( i n t i = 0 ; i < n ; i ++)
f o r ( l i s t <i n t > : : i t e r a t o r j = oldAdj [ i ] . b e g i n ( ) ; j != oldAdj [ i ] .
end ( ) ; j ++) {
a d j [ ∗ j ] . push_front ( i ) ;
54
M[ i ] [ ∗ j ] = j ;
55
56
}
57
58
delete
[ ] oldAdj ;
Capítulo 9. Anexo
59
}
60
61
Digraph : : ~ Digraph ( ) {
62
// L i b e r a memoria
63
f o r ( i n t i = 0 ; i < n ; i ++)
delete
64
[ ] M[ i ] ;
65
delete
[ ] M;
66
delete
[ ] adj ;
67
}
68
69
// I n s e r e o a r c o ( u , v )
70
b o o l Digraph : : i n s e r t _ a r c ( i n t u , i n t v ) {
i f (M[ u ] [ v ] == a d j [ u ] . end ( ) ) {
71
a d j [ u ] . push_front ( v ) ;
72
73
// A t u a l i z a a m a t r i z
74
M[ u ] [ v ] = a d j [ u ] . b e g i n ( ) ;
75
return true ;
76
}
77
78
return f a l s e ;
79
80
}
81
82
// Muda a direcÃ£o de um a r c o em tempo c o n s t a n t e
83
b o o l Digraph : : i n v e r t _ a r c ( i n t u , i n t v )
84
{
85
86
i f (M[ u ] [ v ] == a d j [ u ] . end ( ) | | M[ v ] [ u ] != a d j [ v ] . end ( ) )
return f a l s e ;
87
88
a d j [ u ] . e r a s e (M[ u ] [ v ] ) ;
89
M[ u ] [ v ] = a d j [ u ] . end ( ) ;
90
91
a d j [ v ] . push_front ( u ) ;
M[ v ] [ u ] = a d j [ v ] . b e g i n ( ) ;
84
85
92
return true ;
93
94
}
95
96
// Muda a direcÃ£o dos a r c o s em um caminho u , p [ u ] , p [ p [ u ] ] ,
97
b o o l Digraph : : i n v e r t _ p a t h ( i n t u , c o n s t i n t ∗ p a r e n t )
98
{
...
bool r e s u l t = true ;
99
100
w h i l e ( p a r e n t [ u ] != u ) {
101
102
r e s u l t = r e s u l t && i n v e r t _ a r c ( p a r e n t [ u ] , u ) ;
103
u = parent [ u ] ;
}
104
105
return r esu lt ;
106
107
}
108
109
110
// Remove o a r c o ( u , v ) em tempo c o n s t a n t e
111
b o o l Digraph : : remove_arc ( i n t u , i n t v ) {
112
i f (M[ u ] [ v ] != a d j [ u ] . end ( ) ) {
113
a d j [ u ] . e r a s e (M[ u ] [ v ] ) ;
114
// A t u a l i z a a m a t r i z
115
M[ u ] [ v ] = a d j [ u ] . end ( ) ;
116
return true ;
117
}
118
119
return f a l s e ;
120
121
}
122
123
l i s t <i n t > : : i t e r a t o r Digraph : : r e m o v e _ a r c _ a l t e r n a t i v e ( i n t u , i n t v )
124
{
Capítulo 9. Anexo
l i s t <i n t > : : i t e r a t o r next_element = a d j [ u ] . e r a s e (M[ u ] [ v ] ) ;
125
126
M[ u ] [ v ] = a d j [ u ] . end ( ) ;
127
128
r e t u r n next_element ;
129
130
}
131
132
// V e r i f i c a s e o a r c o ( u , v ) p e r t e n c e ao g r a f o em tempo c o n s t a n t e
133
b o o l Digraph : : e x i s t s _ a r c ( i n t u , i n t v ) {
i f (M[ u ] [ v ] == a d j [ u ] . end ( ) )
134
return f a l s e ;
135
return true ;
136
137
}
138
139
l i s t <i n t > : : i t e r a t o r Digraph : : a r c ( i n t u , i n t v ) {
r e t u r n M[ u ] [ v ] ;
140
141
}
142
143
// Imprime a s l i s t a s de v i z i n h a n c a na t e l a
144
v o i d Digraph : : p r i n t ( ) {
145
f o r ( i n t i = 0 ; i < n ; i ++) {
c o u t << i << " : " ;
146
147
148
// Imprime p r i m e i r o v i z i n h o de i
149
l i s t <i n t > : : i t e r a t o r j = a d j [ i ] . b e g i n ( ) ;
150
i f ( j != a d j [ i ] . end ( ) ) {
c o u t << " " << ∗ j ;
151
152
153
// P e r c o r r e o r e s t a n t e dos v i z i n h o s de i , imprimindo−o s
154
f o r ( j ++; j != a d j [ i ] . end ( ) ; j ++)
c o u t << " , " << ∗ j ;
155
156
157
}
86
87
158
c o u t << e n d l ;
159
}
160
}
161
162
// Le o g r a f o da e n t r a d a e p r e e n c h e a e s t r u t u r a de dados na memoria
163
v o i d Digraph : : read_graph ( FILE ∗ e n t r a d a ) {
while ( ! f e o f ( entrada ) ) {
164
int u , v ;
165
166
167
f s c a n f ( entrada , "%d " , &u ) ;
168
f s c a n f ( entrada , "%d " , &v ) ;
169
170
t h i s −>i n s e r t _ a r c ( u , v ) ;
171
t h i s −>i n s e r t _ a r c ( v , u ) ;
}
172
173
}
174
175
// Le o d i g r a f o da e n t r a d a e p r e e n c h e a e s t r u t u r a de dados na memoria
176
v o i d Digraph : : read_digraph ( FILE ∗ e n t r a d a ) {
while ( ! f e o f ( entrada ) ) {
177
int u , v ;
178
179
180
f s c a n f ( entrada , "%d " , &u ) ;
181
f s c a n f ( entrada , "%d " , &v ) ;
182
t h i s −>i n s e r t _ a r c ( u , v ) ;
183
}
184
185
}
186
187
// R etorna a q u a n t i d a d e de v e r t i c e s
188
i n t Digraph : : get_n ( ) {
return n ;
189
190
}
Capítulo 9. Anexo
88
191
192
/∗ ∗ R etorna a q u a n t i d a d e de a r e s t a s
∗/
193
194
i n t Digraph : : get_m ( ) {
int m = 0;
195
196
f o r ( i n t i = 0 ; i < n ; i ++) {
197
198
l i s t <i n t > : : i t e r a t o r j = a d j [ i ] . b e g i n ( ) ;
199
l i s t <i n t > : : i t e r a t o r f = a d j [ i ] . end ( ) ;
200
f o r ( ; j != f ; j ++)
m ++;
201
}
202
203
r e t u r n m;
204
205
}
206
207
// R etorna um novo g r a f o que e o t r a n s p o s t o do g r a f o −o b j e t o
208
// I am not s u r e we need t h i s f u n c t i o n . . .
209
// s t r o n g l y Conn . comp may s i m p l y t r a n s p o s e t h e same graph G a l l a l o n g
210
Digraph ∗ Digraph : : g e t _ t r a n s p o s e ( ) {
Digraph ∗T = new Digraph ( ∗ t h i s ) ;
211
212
T−>t r a n s p o s e ( ) ;
213
214
r e t u r n T;
215
216
}
217
218
// Aloca e r e t o r n a a m a t r i z de a d j a c e n c i a do g r a f o
219
i n t c o n s t ∗∗ Digraph : : adjacency_matr i x ( ) {
220
221
i f ( matrix != NULL)
r e t u r n ( c o n s t i n t ∗ ∗ ) matrix ;
222
223
matrix = new i n t ∗ [ n ] ;
89
f o r ( i n t i = 0 ; i < n ; i ++)
224
matrix [ i ] = new i n t [ n ] ;
225
226
f o r ( i n t i = 0 ; i < n ; i ++)
227
f o r ( i n t j = 0 ; j < n ; j ++)
228
matrix [ i ] [ j ] = 0 ;
229
230
f o r ( i n t i = 0 ; i < n ; i ++)
231
f o r ( l i s t <i n t > : : i t e r a t o r j = a d j [ i ] . b e g i n ( ) ; j != a d j [ i ] . end ( ) ;
232
j ++)
matrix [ i ] [ ∗ j ] = 1 ;
233
234
r e t u r n ( c o n s t i n t ∗ ∗ ) matrix ;
235
236
}
237
238
#e n d i f /∗ GRAFOS_CPP_ ∗/
codigo/digraph.cpp
1
#pragma once
2
#i f n d e f ARESTA_H_
3
#d e f i n e ARESTA_H_
4
5
s t r u c t Edge {
6
int u , v ;
7
};
8
9
10
#e n d i f /∗ ARESTA_H_ ∗/
codigo/edge.h
1
#pragma once
2
#i f n d e f ISOMORPHISM_H
Capítulo 9. Anexo
3
90
#d e f i n e ISOMORPHISM_H
4
5
#i n c l u d e " d i g r a p h . h "
6
#i n c l u d e " matching . h "
7
#i n c l u d e " p a r t i t i o n . h "
8
9
10
c l a s s Isomorphism {
public :
11
int n ;
12
Digraph ∗G, ∗H;
13
P a r t i t i o n ∗∗ psiG , ∗∗ psiH ;
14
15
Isomorphism ( Digraph ∗G, Digraph ∗H) {
16
t h i s −>G = G;
17
t h i s −>H = H;
18
n = G−>get_n ( ) ;
19
}
20
21
~ Isomorphism ( ) {
f o r ( i n t p = 0 ; p < n ; p ++)
22
d e l e t e psiG [ p ] ;
23
24
f o r ( i n t q = 0 ; q < n ; q ++)
25
d e l e t e psiH [ q ] ;
26
27
28
delete
[ ] psiG ;
29
delete
[ ] psiH ;
30
}
31
32
i n t ∗ matching_based_algorithm ( ) ;
33
34
i n t ∗ get_map_from_two_discrete_partitions ( P a r t i t i o n ∗P , P a r t i t i o n ∗Q)
;
91
35
/∗ Supoe | E(G) | = | E(H) | .
36
∗/
b o o l check_isomorphism ( c o n s t i n t ∗ p e r m u t a t i o n ) ;
37
38
/∗ Remove a r e s t a s de R que nÃ£o e s t a o c o n t i d a s em c i r c u i t o s .
39
∗/
Edge trim_edges ( Digraph ∗R) ;
40
41
42
v o i d r e s t r i c t _ m a t c h i n g ( Matching ∗M, i n t p , i n t q ) ;
43
v o i d r e s t r i c t _ c o m p a t i b i l i t y _ g r a p h ( Digraph ∗R, i n t p , i n t q ) ;
44
Digraph ∗ n e w _ c o n s t r a i n e d _ c o m p a t i b i l i t y _ g r a p h ( Digraph ∗R, i n t p , i n t
q) ;
45
i n t ∗ enumerate_isomorphism_candidates ( Digraph ∗D, Matching ∗M) ;
46
47
};
48
49
#e n d i f
/∗ ISOMORPHISM_H ∗/
codigo/isomorphism.h
1
#i n c l u d e <c s t d l i b >
2
#i n c l u d e <i o s t r e a m >
3
#i n c l u d e " edge . h "
4
#i n c l u d e " s e a r c h . h "
5
#i n c l u d e " isomorphism . h "
6
#i n c l u d e " s i m u l a t i o n . h "
7
8
i n t ∗ Isomorphism : : get_map_from_two_discrete_partitions ( P a r t i t i o n ∗P ,
P a r t i t i o n ∗Q) {
9
i n t ∗ p e r m u t a t i o n = new i n t [ n ] ;
10
11
l i s t <C e l l ∗ >:: i t e r a t o r i = P−> c e l l s . b e g i n ( ) , j = Q−> c e l l s . b e g i n ( ) ,
l a s t _ i = P−> c e l l s . end ( ) ;
12
13
f o r ( ; i != l a s t _ i ; i ++, j ++)
p e r m u t a t i o n [ ∗ ( ( ∗ i )−>v e r t i c e s . b e g i n ( ) ) ] = ∗ ( ( ∗ j )−>v e r t i c e s . b e g i n ( ) ) ;
Capítulo 9. Anexo
92
14
r et u r n permutation ;
15
16
17
}
18
19
/∗ Recebe d o i s g r a f o s e uma n−permutaÃ§ao . Supoe que o s
20
∗ g r a f o s r e c e b i d o s tem n v e r t i c e s e supoe que o s g r a f o s
21
∗ r e c e b i d o s possuem o mesmo nÃºmero de a r e s t a s .
22
∗/
b o o l Isomorphism : : check_isomorphism ( c o n s t i n t ∗ p e r m u t a t i o n ) {
23
i n t n = G−>get_n ( ) ;
24
c o n s t i n t ∗∗MH = H−>adjacency_matr i x ( ) ;
25
l i s t <i n t > ∗ a d j = G−>a d j ;
26
f o r ( i n t u = 0 ; u < n ; u++)
27
f o r ( l i s t <i n t > : : i t e r a t o r v = a d j [ u ] . b e g i n ( ) ; v != a d j [ u ] . end ( ) ; v
28
++)
if
29
( !MH[ p e r m u t a t i o n [ u ] ] [ p e r m u t a t i o n [ ∗ v ] ] )
return f a l s e ;
30
31
return true ;
32
33
}
34
35
36
37
38
39
/∗ Devolve um i s o m o r f i s m o de G em H (em forma de um
∗ v e t o r de permutaÃ§ao ) ou NULL. ∗/
i n t ∗ Isomorphism : : matching_based_algorithm ( ) {
i f (H−>get_n ( ) != G−>get_n ( ) | | H−>get_m ( ) != G−>get_m ( ) )
r e t u r n NULL;
40
41
psiG = new P a r t i t i o n ∗ [ n ] ;
42
psiH = new P a r t i t i o n ∗ [ n ] ;
43
44
// C a l c u l a a p a r t i Ã § a o da p−simulaÃ§ao para todo p em V(G)
45
f o r ( i n t p = 0 ; p < n ; p++) {
93
46
// Faz a p−simulaÃ§ao para cada p em V(G)
47
psiG [ p ] = S i m u l a t i o n (G, p ) . g e t _ p a r t i t i o n ( ) ;
48
49
// Se a p a r t i Ã § a o o b t i d a e d i s c r e t a , s e r a r a p i d o . . .
50
i f ( psiG [ p]−> i s _ d i s c r e t e ( ) ) {
51
52
// Faz a q−simulaÃ§ao para cada q em V(H)
53
f o r ( i n t q = 0 ; q < n ; q++) {
psiH [ q ] = S i m u l a t i o n (H, q ) . g e t _ p a r t i t i o n ( ) ;
54
55
56
// Se uma p a r t i Ã § a o o b t i d a e d i s c r e t a , t e s t a por i s o m o r f i s m o
57
i f ( psiH [ q]−> i s _ d i s c r e t e ( ) ) {
i n t ∗ p e r m u t a t i o n = get_map_from_two_discrete_partitions ( psiG [
58
p ] , psiH [ q ] ) ;
59
i f ( check_isomorphism ( p e r m u t a t i o n ) )
60
r et u r n permutation ;
61
62
delete
63
[ ] permutation ;
}
64
}
65
66
67
// Nao e x i s t e i s o m o r f i s m o e n t r e G e H
68
r e t u r n NULL;
}
69
70
}
71
72
// C a l c u l a a p a r t i Ã § a o da q−simulaÃ§ao para todo q em V(H)
73
f o r ( i n t q = 0 ; q < n ; q++) {
74
psiH [ q ] = S i m u l a t i o n (H, q ) . g e t _ p a r t i t i o n ( ) ;
75
76
// Se a p a r t i Ã § a o o b t i d a e d i s c r e t a , nao e x i s t e i s o m o r f i s m o e n t r e G
e H
Capítulo 9. Anexo
i f ( psiH [ q]−> i s _ d i s c r e t e ( ) )
77
r e t u r n NULL;
78
}
79
80
81
// Gera g r a f o R
82
Digraph ∗R = new Digraph ( 2 ∗ n ) ;
83
f o r ( i n t p = 0 ; p < n ; p++)
f o r ( i n t q = 0 ; q < n ; q++)
84
i f ( psiG [ p]−> i s _ c o m p a t i b l e ( psiH [ q ] ) )
85
R−>i n s e r t _ a r c ( q + n , p ) ;
86
87
88
//
R−>p r i n t ( ) ;
89
Matching ∗M = new Matching ( n ) ;
90
M−>grow_matching_in (R) ;
91
i f (M−>i s _ p e r f e c t ( ) ) {
i n t ∗ p e r m u t a t i o n = enumerate_isomorphism_candidates (R, M) ;
92
93
94
d e l e t e R;
95
d e l e t e M;
96
r et u r n permutation ;
97
}
98
99
100
d e l e t e M;
101
d e l e t e R;
102
r e t u r n NULL;
103
104
}
105
106
v o i d Isomorphism : : r e s t r i c t _ m a t c h i n g ( Matching ∗M, i n t p , i n t q ) {
107
c o n s t i n t ∗ G_p_cell_of_vertex = psiG [ p]−> c e l l _ o f _ v e r t e x _ a r r a y ( ) ;
108
c o n s t i n t ∗ H_q_cell_of_vertex = psiH [ q]−> c e l l _ o f _ v e r t e x _ a r r a y ( ) ;
109
c o n s t i n t ∗ matched = M−>mapping ( ) ;
94
95
110
f o r ( i n t i = 0 ; i < n ; i ++) {
111
i f ( matched [ i ] == NOONE)
112
continue ;
113
114
115
i n t j = matched [ i ] ;
116
c o n s t i n t ∗ G_i_cell_of_vertex = psiG [ i ]−> c e l l _ o f _ v e r t e x _ a r r a y ( ) ;
117
c o n s t i n t ∗ H_j_cell_of_vertex = psiH [ j ]−> c e l l _ o f _ v e r t e x _ a r r a y ( ) ;
118
i f ( G_p_cell_of_vertex [ i ] != H_q_cell_of_vertex [ j ] )
119
M−>set_matched ( i , NOONE) ;
120
121
i f ( G_i_cell_of_vertex [ p ] != H_j_cell_of_vertex [ q ] )
122
M−>set_matched ( i , NOONE) ;
123
}
124
125
}
126
127
128
/∗ p and q must be i n t h e r a n g e 0 . . ( n−1) . ∗/
129
Digraph ∗ Isomorphism : : n e w _ c o n s t r a i n e d _ c o m p a t i b i l i t y _ g r a p h ( Digraph ∗R,
int p , int q) {
130
Digraph ∗S = new Digraph ( 2 ∗ n ) ;
131
c o n s t i n t ∗ G_p_cell_of_vertex = psiG [ p]−> c e l l _ o f _ v e r t e x _ a r r a y ( ) ;
132
c o n s t i n t ∗ H_q_cell_of_vertex = psiH [ q]−> c e l l _ o f _ v e r t e x _ a r r a y ( ) ;
133
134
f o r ( i n t i = 0 ; i < n ; i ++) {
135
c o n s t i n t ∗ G_i_cell_of_vertex = psiG [ i ]−> c e l l _ o f _ v e r t e x _ a r r a y ( ) ;
136
l i s t <i n t > &n e i g h b o r s = R−>a d j [ i ] ;
137
138
f o r ( l i s t <i n t > : : i t e r a t o r j = n e i g h b o r s . b e g i n ( ) ; j != n e i g h b o r s . end
( ) ; j ++) {
139
c o n s t i n t ∗ H_j_cell_of_vertex = psiH [ ∗ j − n]−>
cell_of_vertex_array ( ) ;
Capítulo 9. Anexo
96
140
i f ( G_p_cell_of_vertex [ i ] == H_q_cell_of_vertex [ ∗ j − n ] )
141
i f ( G_i_cell_of_vertex [ p ] == H_j_cell_of_vertex [ q ] )
142
S−>i n s e r t _ a r c ( i , ∗ j ) ;
143
}
144
}
145
146
f o r ( i n t i = 0 ; i < n ; i ++) {
147
148
c o n s t i n t ∗ H_i_cell_of_vertex = psiH [ i ]−> c e l l _ o f _ v e r t e x _ a r r a y ( ) ;
149
l i s t <i n t > &n e i g h b o r s = R−>a d j [ i + n ] ;
150
f o r ( l i s t <i n t > : : i t e r a t o r j = n e i g h b o r s . b e g i n ( ) ; j != n e i g h b o r s . end
151
( ) ; j ++) {
c o n s t i n t ∗ G_j_cell_of_vertex = psiG [ ∗ j ]−> c e l l _ o f _ v e r t e x _ a r r a y ( ) ;
152
153
154
i f ( G_p_cell_of_vertex [ ∗ j ] == H_q_cell_of_vertex [ i ] )
155
i f ( G_j_cell_of_vertex [ p ] == H_i_cell_of_vertex [ q ] )
S−>i n s e r t _ a r c ( i + n , ∗ j ) ;
156
}
157
}
158
159
return S ;
160
161
}
162
163
164
165
166
/∗ Remove a r e s t a s que nao e s t a o em c i r c u i t o s e r e t o r n a a
∗ Ãºltima a r e s t a que nao f o i removida .
Edge Isomorphism : : trim_edges ( Digraph ∗D) {
Edge e = {NOONE, NOONE} ;
167
168
S e a r c h S (D) ;
169
S . strongly_connec te d_co m po nent s _al g o ri t hm ( ) ;
170
i n t const ∗ scc = S . get_scc_array ( ) ;
171
∗/
97
f o r ( i n t i = 0 ; i < n ; i ++) {
172
l i s t <i n t > &n e i g h b o r s = D−>a d j [ i ] ;
173
174
f o r ( l i s t <i n t > : : i t e r a t o r j = n e i g h b o r s . b e g i n ( ) ; j != n e i g h b o r s . end
175
( ) ; j ++)
i f ( s c c [ i ] != s c c [ ∗ j ] ) {
176
177
j = D−>r e m o v e _ a r c _ a l t e r n a t i v e ( i , ∗ j ) ;
178
i f ( j == n e i g h b o r s . end ( ) )
break ;
179
180
}
181
else {
182
e .u = i ;
183
e.v = ∗j ;
}
184
}
185
186
return e ;
187
188
}
189
190
/∗ Recebe um g r a f o b i p a r t i d o b a l a n c e a d o R e um emp . p e r f e i t o M.
191
i n t ∗ Isomorphism : : enumerate_isomorphism_candidates ( Digraph ∗D, Matching
∗M) {
192
193
i f ( check_isomorphism (M−>mapping ( ) ) ) {
194
i n t ∗ p e r m u t a t i o n = new i n t [ n ] ;
195
c o n s t i n t ∗ mapping = M−>mapping ( ) ;
196
f o r ( i n t i = 0 ; i < n ; i ++)
197
p e r m u t a t i o n [ i ] = mapping [ i ] ;
198
199
r et u r n permutation ;
200
201
202
}
∗/
Capítulo 9. Anexo
203
98
Edge e , e_prime = trim_edges (D) ;
204
205
i f ( e_prime . u == NOONE)
r e t u r n NULL;
206
207
208
/∗ Acha c i r c u i t o C . ∗/
209
S e a r c h S (D) ;
210
S . find_path ( e_prime . v , e_prime . u ) ;
211
i n t c o n s t ∗ path = S . get_parent_array ( ) ;
212
213
/∗ E s c o l h e a a r e s t a e . ∗/
214
i f ( e_prime . u < e_prime . v )
e = e_prime ;
215
216
else {
217
e . v = e_prime . u ;
218
e . u = path [ e_prime . u ] ;
219
}
220
221
Matching ∗M_prime = new Matching (M, e_prime . u , path ) ;
222
223
Digraph ∗ D_plus = n e w _ c o n s t r a i n e d _ c o m p a t i b i l i t y _ g r a p h (D, e . u , e . v − n
);
224
225
r e s t r i c t _ m a t c h i n g (M, e . u , e . v − n ) ;
226
227
M−>grow_matching_in ( D_plus ) ;
228
229
i f (M−>i s _ p e r f e c t ( ) ) {
230
231
i n t ∗ p e r m u t a t i o n = enumerate_isomorphism_candidates ( D_plus , M) ;
232
233
i f ( permutation ) {
234
d e l e t e D_plus ;
99
d e l e t e M_prime ;
235
236
r et u r n permutation ;
237
}
238
239
}
240
241
d e l e t e D_plus ;
242
243
244
D−>i n v e r t _ p a t h ( e_prime . u , path ) ;
245
D−>i n v e r t _ a r c ( e_prime . u , e_prime . v ) ;
246
247
/∗ Remove o a r c o r e v e r s o de e ( p o i s e f o i r e v e r t i d o ) .
248
D−>r e m o v e _ a r c _ a l t e r n a t i v e ( e . v , e . u ) ;
∗/
249
i n t ∗ p e r m u t a t i o n = enumerate_isomorphism_candidates (D, M_prime ) ;
250
251
d e l e t e M_prime ;
252
253
i f ( permutation )
254
r et u r n permutation ;
255
256
r e t u r n NULL;
257
258
}
codigo/isomorphism.cpp
1
#i n c l u d e <c s t d l i b >
2
#i n c l u d e <f s t r e a m >
3
#i n c l u d e <i o s t r e a m >
4
#i n c l u d e " isomorphism . h "
5
6
7
u s i n g namespace s t d ;
Capítulo 9. Anexo
8
9
100
i n t main ( i n t ac , c h a r ∗∗ av ) {
int n ;
10
11
// MABI −− matching based isomorphism
12
i f ( ac != 3 ) {
13
c o u t << " Usage : \ n\n\ tmabi <graph f i l e #1> <graph f i l e #2>\n\n " ;
14
c o u t << " \ t \ t−− t h e format o f a graph f i l e
15
c o u t << " n a_1 b_1 a_2 b_2 . . . a_m b_m EOF, \ n\ t \ t " ;
16
c o u t << " where a_i b_i e n c o d e s an edge , and numbers\n\ t \ t " ;
17
c o u t << " a r e s e p a r a t e d by w h i t e s p a c e s \n\n " ;
i s : \ n\ t \ t " ;
18
r e t u r n EXIT_FAILURE ;
19
20
}
21
22
// Entrada dos g r a f o s G e H
23
FILE ∗ graph1 = f o p e n ( av [ 1 ] , " r t " ) ;
24
i f ( graph1 == NULL) {
25
c o u t << " Could not open graph f i l e " << av [ 1 ] << e n d l ;
26
r e t u r n EXIT_FAILURE ;
27
}
28
29
f s c a n f ( graph1 , "%d " , &n ) ;
30
Digraph ∗G = new Digraph ( n ) ;
31
G−>read_graph ( graph1 ) ;
32
f c l o s e ( graph1 ) ;
33
34
35
FILE ∗ graph2 = f o p e n ( av [ 2 ] , " r t " ) ;
i f ( graph2 == NULL) {
36
c o u t << " Could not open graph f i l e " << av [ 2 ] << e n d l ;
37
r e t u r n EXIT_FAILURE ;
38
}
39
40
f s c a n f ( graph2 , "%d " , &n ) ;
101
41
Digraph ∗H = new Digraph ( n ) ;
42
H−>read_graph ( graph2 ) ;
f c l o s e ( graph2 ) ;
43
44
Isomorphism I (G, H) ;
45
46
47
i n t ∗ p e r m u t a t i o n = I . matching_based_algorithm ( ) ;
48
i f ( permutation ) {
f o r ( i n t i = 0 ; i < n − 1 ; i ++)
49
c o u t << p e r m u t a t i o n [ i ] << " " ;
50
c o u t << p e r m u t a t i o n [ n − 1 ] << e n d l ;
51
}
52
53
54
d e l e t e G;
55
d e l e t e H;
56
return 0;
57
58
}
codigo/main.cpp
1
2
#pragma once
3
#i f n d e f MATCHING_H
4
#d e f i n e MATCHING_H
5
6
#i f n d e f NOONE
7
#d e f i n e NOONE −1
8
#e n d i f
9
10
#i f n d e f NULL
11
#d e f i n e NULL 0
12
#e n d i f
13
Capítulo 9. Anexo
14
102
#i n c l u d e " edge . h "
15
16
c l a s s Digraph ;
17
18
/∗ C l a s s e r e s p o n s a v e l por e n c o n t r a r um emparelhamento
19
∗ p e r f e i t o num g r a f o b i p a r t i d o b a l a n c e a d o ( p o s s u i n d o
20
∗ v e r t i c e s de 0 a ( k − 1 ) de um lado , e de k a ( 2 k −
21
∗ 1 ) do o u t r o .
22
c l a s s Matching {
23
private :
24
25
/∗ n = 2 k
∗/
∗/
int k , n ;
26
27
Digraph ∗D;
28
29
30
31
/∗ Vetor com k p o s i Ã § o e s : matched [ i ] = v e r t i c e ao q u a l
∗ i e s t a emparelhado ou NOONE c a s o c o n t r a r i o .
∗/
i n t ∗ matched ;
32
33
34
35
/∗ Vetor com 2k e l e m e n t o s usado para g u a r d a r
∗ caminhos da busca .
∗/
i n t ∗ parent ;
36
37
/∗ FunÃ§ao r e c u r s i v a de busca em p r o f u n d i d a d e : a
38
∗ busca t e r m i n a quando e n c o n t r a r um v e r t i c e i
39
∗ nao s a t u r a d o ( sem a r c o s a i n d o ) do l a d o menor
40
∗ ( i . e . com i < k ) .
41
int dfs_visit ( int i ) ;
∗/
42
43
44
45
46
public :
/∗ Supoe que o g r a f o H e b i p a r t i d o , com v e r t i c e s
∗ de 0 a t e ( k−1) de um dos l a d o s .
Matching ( i n t k ) ;
∗/
103
47
Matching ( c o n s t Matching &M) ;
48
49
Matching ( Matching ∗M, i n t edge_bottom , c o n s t i n t ∗ path ) ;
50
51
~ Matching ( ) ;
52
53
54
/∗ Encontra um emparelhamento maximo no g r a f o .
55
v o i d grow_matching_in ( Digraph ∗H) ;
∗/
56
/∗ V e r i f i c a s e o emparelhamento e p e r f e i t o .
57
∗/
bool is_ p erfect () ;
58
59
/∗ Imprime emparelhamento .
60
∗/
void p r i n t ( ) ;
61
62
63
/∗ R etorna mapa c o r r e s p o n d e n t e ao emparelhamento .
64
c o n s t i n t ∗ mapping ( ) ;
65
/∗ A j u s t a manualmente um v e r t i c e emparelhado a o u t r o
66
∗ ( s o no v e t o r matched ) .
67
v o i d set_matched ( i n t i , i n t j ) ;
68
69
∗/
};
70
71
72
#e n d i f
/∗ MATCHING_H ∗/
codigo/matching.h
1
#i n c l u d e < l i s t >
2
#i n c l u d e <v e c t o r >
3
#i n c l u d e " s e a r c h . h "
4
#i n c l u d e " d i g r a p h . h "
5
#i n c l u d e " matching . h "
∗/
Capítulo 9. Anexo
104
6
7
Matching : : Matching ( i n t k ) {
D = NULL;
8
t h i s −>k = k ;
9
10
n = 2 ∗ k;
11
matched = new i n t [ k ] ;
12
p a r e n t = NULL;
13
f o r ( i n t i = 0 ; i < k ; i ++)
14
matched [ i ] = NOONE;
15
16
}
17
18
Matching : : Matching ( c o n s t Matching &M) {
19
D = NULL;
20
k = M. k ;
21
n = M. n ;
22
matched = new i n t [ k ] ;
23
p a r e n t = NULL;
24
f o r ( i n t i = 0 ; i < k ; i ++)
25
matched [ i ] = M. matched [ i ] ;
26
27
}
28
29
/∗ Faz uma c o p i a do emparelhamento M e f a z M = M ds C, onde
30
∗ ds denota a ’ d i f e r e n c a s i m e t r i c a ’ e C e o c i r c u i t o c o d i −
31
∗ f i c a d o p e l o v e r t i c e edge_bottom e p e l o caminho c o d i f i c a −
32
∗ do na a r v o r e de busca ’ path ’ .
33
∗/
Matching : : Matching ( Matching ∗M, i n t edge_bottom , c o n s t i n t ∗ path ) {
34
D = NULL;
35
k = M−>k ;
36
n = M−>n ;
37
matched = new i n t [ k ] ;
38
p a r e n t = NULL;
105
39
f o r ( i n t i = 0 ; i < k ; i ++)
40
matched [ i ] = M−>matched [ i ] ;
41
42
/∗ ∗∗∗∗∗∗∗∗ ∗∗ ∗ ∗ ∗∗ ∗ ∗ ∗ ∗∗ ∗ ∗ ∗∗ ∗ CHECK CHECK CHECK CHECK ∗∗∗∗∗∗∗∗∗∗ ∗∗ ∗ ∗∗ ∗ ∗
43
∗/
44
i n t x = edge_bottom ;
45
w h i l e ( path [ x ] != x ) {
46
matched [ x ] = path [ x ] − k ;
47
x = path [ path [ x ] ] ;
}
48
49
}
50
51
Matching : : ~ Matching ( ) {
52
delete
53
i f ( p a r e n t != NULL)
delete
54
55
[ ] matched ;
[ ] parent ;
}
56
57
/∗ Funcao r e c u r s i v a de busca em p r o f u n d i d a d e .
58
∗ Busca t e r m i n a quando e n c o n t r a r um v e r t i c e
59
∗ i < k , sem a r c o de s a Ã d a .
60
61
62
i n t Matching : : d f s _ v i s i t ( i n t i ) {
i f ( i < k && matched [ i ] == NOONE)
return i ;
63
64
l i s t <i n t > : : i t e r a t o r j = D−>a d j [ i ] . b e g i n ( ) ;
65
l i s t <i n t > : : i t e r a t o r end = D−>a d j [ i ] . end ( ) ;
66
f o r ( ; j != end ; j ++)
67
i f ( p a r e n t [ ∗ j ] == NOONE) {
68
parent [ ∗ j ] = i ;
69
i n t r = d f s _ v i s i t (∗ j ) ;
70
i f ( r != NOONE)
∗/
Capítulo 9. Anexo
106
return r ;
71
}
72
73
r e t u r n NOONE;
74
75
}
76
77
/∗ Encontra um emparelhamento maximo no g r a f o H dado . Caso o
78
∗ emparelhamento j a tenha s i d o e n c o n t r a d o a n t e r i o r m e n t e s o b r e o mesmo
79
∗ g r a f o ou s o b r e um s u p e r g r a f o d e l e , ou ainda , s e o emparelhamento
80
∗ f o i c r i a d o a p a r t i r de uma c o p i a de o u t r o emparelhamento
81
∗ ( p o s s i v e l m e n t e d e s a t u a l i z a d o ) , e f e i t a uma v e r i f i c a c a o para
82
∗ e n c o n t r a r p o s s Ã v e i s i r r e g u l a r i d a d e s . Por exemplo , s e um v e r t i c e
83
∗ e s t a emparelhado com um c e r t o v e r t i c e segundo o v e t o r ’ matched ’ ,
84
∗ mas com um v e r t i c e d i f e r e n t e no g r a f o H, i s s o deve s e r c o r r i g i d o
85
∗ ( a t u a l i a n d o −s e o v e t o r matched ) . Caso um v e r t i c e i e s t e j a
86
∗ emparelhado com um v e r t i c e j segundo o v e t o r ’ matched ’ mas nao
87
∗ e s t e j a emparelhado com ninguem no g r a f o H, e n t a o tudo bem , d e s d e
88
∗ que i e j nao tenham a r c o s i n c i d e n t e s no g r a f o . Essa v e r i f i c a c a o
89
∗ nao e f e i t a a t u a l m e n t e . Tambem supoe−s e que o g r a f o H nao p o s s u i
90
∗ v e r t i c e na p a r t e de b a i x o ( de 0 a ( k − 1 ) ) com mais de um a r c o
91
∗ de s a Ã d a .
92
93
∗/
v o i d Matching : : grow_matching_in ( Digraph ∗H) {
D = H;
94
95
96
97
f o r ( i n t i = 0 ; i < k ; i ++) {
l i s t <i n t > &n e i g h b o r s = D−>a d j [ i ] ;
98
99
100
101
// p e n s a r s e i s s o pode o c o r r e r :
i f ( n e i g h b o r s . b e g i n ( ) != n e i g h b o r s . end ( ) )
matched [ i ] = ∗ ( n e i g h b o r s . b e g i n ( ) ) − k ;
102
103
/∗ Se o g r a f o de e n t r a d a nao t i v e r no maximo um a r c o s a i n d o
107
104
∗ de cada v e r t i c e da p a r t e de ’ b a i x o ’ , e n t a o a l i n h a acima
105
∗ e onde c o r r e −s e o r i s c o de t e r matched [ i ] = matched [ j ]
106
∗ com i != j . ∗/
107
}
108
109
110
111
112
i f ( p a r e n t == NULL)
p a r e n t = new i n t [ n ] ;
113
114
b o o l augmented ;
115
116
/∗ Guarda s e um v e r t i c e de k a t e n − 1 e s t a s a t u r a d o ou nao .
117
i n t ∗ s = new i n t [ k ] ;
118
119
120
f o r ( i n t i = 0 ; i < k ; i ++)
s [ i ] = NOONE;
121
122
123
f o r ( i n t i = 0 ; i < k ; i ++)
i f ( matched [ i ] != NOONE)
s [ matched [ i ] ] = i ;
124
125
126
127
do {
augmented = f a l s e ;
128
129
130
f o r ( i n t i = 0 ; i < n ; i ++)
p a r e n t [ i ] = NOONE;
131
132
133
f o r ( i n t i = 0 ; i < k ; i ++) {
int j = i + k ;
134
135
136
i f ( s [ i ] == NOONE) {
parent [ j ] = j ;
∗/
Capítulo 9. Anexo
s [ i ] = dfs_visit ( j ) ;
137
}
138
}
139
140
f o r ( i n t i = 0 ; i < k ; i ++) {
141
i f ( s [ i ] == NOONE | | matched [ s [ i ] ] == i )
142
continue ;
143
144
/∗ R e a l i z a a i n v e r s a o da o r i e n t a c a o dos a r c o s num caminho
145
∗ aumentador de i a t e s [ i ] . ∗/
146
f o r ( i n t j = s [ i ] ; p a r e n t [ j ] != j ; j = p a r e n t [ j ] ) {
147
i f ( j < k) {
148
149
matched [ j ] = p a r e n t [ j ] − k ;
150
s [ matched [ j ] ] = j ;
151
}
152
D−>i n v e r t _ a r c ( p a r e n t [ j ] , j ) ;
}
153
154
augmented = t r u e ;
155
}
156
} w h i l e ( augmented ) ;
157
158
delete
159
160
[] s;
}
161
162
v o i d Matching : : p r i n t ( ) {
f o r ( i n t i = 0 ; i < k ; i ++)
163
c o u t << i << " : " << matched [ i ] << e n d l ;
164
165
}
166
167
b o o l Matching : : i s _ p e r f e c t ( ) {
168
f o r ( i n t i = 0 ; i < k ; i ++)
169
i f ( matched [ i ] == NOONE)
108
109
return f a l s e ;
170
171
return true ;
172
173
}
174
175
c o n s t i n t ∗ Matching : : mapping ( ) {
r e t u r n ( c o n s t i n t ∗ ) matched ;
176
177
}
178
179
v o i d Matching : : set_matched ( i n t i , i n t j ) {
matched [ i ] = j ;
180
181
}
codigo/matching.cpp
1
#pragma once
2
#i f n d e f PARTICAO_H_
3
#d e f i n e PARTICAO_H_
4
5
#i n c l u d e " c e l l . h "
6
#i n c l u d e <map>
7
#i n c l u d e < l i s t >
8
9
u s i n g namespace s t d ;
10
11
// C l a s s e para armazenar dados de uma p a r t i c a o
12
class Partition {
13
private :
14
int n ;
15
int ∗ cell_of_vertex ;
16
b o o l cell_of_vertex_array_up_to_date ;
17
18
19
public :
l i s t <C e l l ∗> c e l l s ;
// Guarda a l i s t a ordenada de c e l u l a s
Capítulo 9. Anexo
110
20
21
const in t ∗ cell_of_vertex_array ( ) ;
22
bool i s _ d i s c r e t e () ;
23
b o o l i s _ c o m p a t i b l e ( P a r t i t i o n ∗P) ;
24
bool r efin e_ or d er ed _ p ar t it ion _ u sin g_ lab els ( i n t ∗) ;
25
void p r i n t ( ) ;
26
int size () ;
27
28
Partition ( int n) ;
29
~Partition () ;
30
};
31
32
33
34
#e n d i f /∗ PARTICAO_H_ ∗/
codigo/partition.h
1
#i f n d e f PARTICAO_CPP_
2
#d e f i n e PARTICAO_CPP_
3
4
#i f n d e f NULL
5
#d e f i n e NULL 0
6
#e n d i f
7
8
#i n c l u d e < l i s t >
9
#i n c l u d e <s e t >
10
#i n c l u d e <map>
11
#i n c l u d e " p a r t i t i o n . h "
12
13
u s i n g namespace s t d ;
14
15
/∗ I n i c i a l i z a uma p a r t i c a o u n i t a r i a do c o n j u n t o { 0 , . . . , n − 1} ∗/
16
Partition : : Partition ( int n) {
111
17
C e l l ∗C = new C e l l ( 0 ) ;
18
t h i s −>n = n ;
19
f o r ( i n t i = 0 ; i < n ; i ++)
20
C−>v e r t i c e s . i n s e r t ( i ) ;
21
22
23
c e l l s . push_back (C) ;
24
c e l l _ o f _ v e r t e x = NULL;
25
cell_of_vertex_array_up_to_date = f a l s e ;
26
}
27
28
Partition ::~ Partition () {
i f ( cell_of_vertex )
29
delete
30
[ ] cell_of_vertex ;
31
w h i l e ( ! c e l l s . empty ( ) ) {
32
33
C e l l ∗C = c e l l s . f r o n t ( ) ;
34
c e l l s . pop_front ( ) ;
35
d e l e t e C;
36
}
37
38
}
39
40
41
42
b o o l P a r t i t i o n : : i s _ c o m p a t i b l e ( P a r t i t i o n ∗P) {
i f ( c e l l s . s i z e ( ) != P−> c e l l s . s i z e ( ) )
return f a l s e ;
43
44
l i s t <C e l l ∗ >:: i t e r a t o r i , j ;
45
f o r ( i = c e l l s . b e g i n ( ) , j = P−> c e l l s . b e g i n ( ) ; i != c e l l s . end ( ) ; i
++, j ++) {
46
47
48
i f ( ( ∗ i )−>l a b e l != ( ∗ j )−>l a b e l )
return f a l s e ;
i f ( ( ∗ i )−>v e r t i c e s . s i z e ( ) != ( ∗ j )−>v e r t i c e s . s i z e ( ) )
Capítulo 9. Anexo
112
return f a l s e ;
49
}
50
51
return true ;
52
53
}
54
55
bool Partition : : i s _ d i s c r e t e () {
r e t u r n ( c e l l s . s i z e ( ) == ( u n s i g n e d ) n ) ;
56
57
}
58
59
const in t ∗ Part it ion : : cell_of_vertex_array ( ) {
i f ( c e l l _ o f _ v e r t e x == NULL)
60
c e l l _ o f _ v e r t e x = new i n t [ n ] ;
61
62
if
63
( ! cell_of_vertex_array_up_to_date ) {
64
int k = 0;
65
f o r ( l i s t <C e l l ∗ >:: i t e r a t o r i = c e l l s . b e g i n ( ) ; i != c e l l s . end ( )
; i ++, k++)
f o r ( s e t <i n t > : : i t e r a t o r j = ( ∗ i )−>v e r t i c e s . b e g i n ( ) ; j != ( ∗
66
i )−>v e r t i c e s . end ( ) ; j ++)
cell_of_vertex [∗ j ] = k ;
67
68
cell_of_vertex_array_up_to_date = t r u e ;
69
}
70
71
r et u r n ( const i n t ∗) cell_ of_ v er t ex ;
72
73
}
74
75
76
77
/∗ Devolve ’ t r u e ’ s e o r e f i n a m e n t o i n d u z i d o p e l o v e t o r ’ l a b e l ’
∗ e nao t r i v i a l e ’ f a l s e ’ c a s o c o n t r a r i o
∗/
bool Partition : : refine_ordered_partition_using_labels ( in t ∗ l a b e l ) {
78
bool r e f i n e d = f a l s e ;
79
l i s t <C e l l ∗> n e w _ c e l l s ;
113
80
81
f o r ( l i s t <C e l l ∗ >:: i t e r a t o r i = c e l l s . b e g i n ( ) ; i != c e l l s . end ( ) ; i
++) {
map<i n t , C e l l ∗> c h i l d r e n ;
82
83
84
f o r ( s e t <i n t > : : i t e r a t o r j = ( ∗ i )−>v e r t i c e s . b e g i n ( ) ; j != ( ∗ i )−>
v e r t i c e s . end ( ) ; j ++)
c h i l d r e n [ l a b e l [ ∗ j ] ] = NULL;
85
86
f o r ( s e t <i n t > : : i t e r a t o r j = ( ∗ i )−>v e r t i c e s . b e g i n ( ) ; j != ( ∗ i )−>
87
v e r t i c e s . end ( ) ; j ++) {
// O o p e r a d o r [ ] da c l a s s e
88
’map ’ c r i a uma ’ C e l l ’ s e a chave
nao e s t i v e r l a
i f ( c h i l d r e n [ l a b e l [ ∗ j ] ] == NULL) {
89
c h i l d r e n [ l a b e l [ ∗ j ] ] = new C e l l ( l a b e l [ ∗ j ] ) ;
90
}
91
92
c h i l d r e n [ l a b e l [ ∗ j ]]−> v e r t i c e s . i n s e r t ( ∗ j ) ;
93
94
}
95
96
i f ( c h i l d r e n . s i z e ( ) > 1)
refined = true ;
97
98
99
delete ∗ i ;
100
101
f o r (map<i n t , C e l l ∗ >:: i t e r a t o r k = c h i l d r e n . b e g i n ( ) ; k != c h i l d r e n
. end ( ) ; k ++)
n e w _ c e l l s . push_back ( k−>s e c o n d ) ;
102
103
}
104
105
c e l l s = new_cells ;
106
107
i f ( refined )
Capítulo 9. Anexo
cell_of_vertex_array_up_to_date = f a l s e ;
108
return refined ;
109
110
114
}
111
112
// R etorna a q u a n t i d a d e de c e l u l a s da p a r t i c a o
113
int Partition : : size () {
return c e l l s . siz e () ;
114
115
}
116
117
#e n d i f
codigo/partition.cpp
1
#pragma once
2
#i f n d e f DFS_H_
3
#d e f i n e DFS_H_
4
5
#i n c l u d e < l i s t >
6
#i n c l u d e " d i g r a p h . h "
7
8
#i f n d e f NOONE
9
#d e f i n e NOONE −1
10
#e n d i f
11
12
c l a s s Search {
13
private :
14
int n ;
15
Digraph ∗G;
16
17
i n t component_counter ;
18
19
20
21
/∗ Vetor contendo o nÃºmero da componente f o r t e m e n t e
∗ conexa contendo cada v e r t i c e .
int ∗ scc ;
∗/
115
22
23
24
/∗ Guarda a r v o r e de busca .
∗/
i n t ∗ parent ;
25
26
27
/∗ Guarda l i s t a de v e r t i c e s por tempo de f i n a l i z a c a o .
∗/
l i s t <i n t > v e r t i c e s _ s o r t e d _ b y _ f i n i s h _ t i m e ;
28
29
/∗ Funcao r e c u r s i v a da busca em p r o f u n d i d a d e .
30
void v i s i t ( i n t ) ;
∗/
31
32
/∗ Usada na busca por um caminho ( f u n c a o find_path ) .
33
b o o l visit_u_look_fo r _v ( i n t u , i n t v ) ;
∗/
34
35
36
37
38
public :
/∗ R etorna um v e t o r c com n e l e m e n t o s , onde c [ i ] denota o nÃºmero
∗ da componente da a r v o r e de busca que contem o v e r t i c e i .
∗/
i n t const ∗ get_scc_array ( ) ;
39
40
41
42
/∗ R etorna um v e t o r p com n e l e m e n t o s , onde p [ i ] denota o v e r t i c e
∗ que e p a i do v e r t i c e i na a r v o r e de busca em p r o f u n d i d a d e .
i n t c o n s t ∗ get_parent_array ( ) ;
43
44
S e a r c h ( Digraph ∗G) ;
45
~ Search ( ) ;
46
47
48
49
/∗ I n i c i a l i z a parÃ¢metros da busca . Limpa a l i s t a de v e r t i c e s
∗ o r d e n a d o s por tempo de f i n a l i z a c a o .
∗/
void r e s e t ( ) ;
50
51
52
53
54
/∗ Executa busca em p r o f u n d i d a d e . P r o c e s s a o s v e r t i c e s no l a c o
∗ p r i n c i p a l segundo a ordem d e s e j a d a .
v o i d d f s ( l i s t <i n t > &o r d e r ) ;
void d fs ( ) ;
∗/
∗/
Capítulo 9. Anexo
116
55
/∗ Executa o a l g o r i t m o que e n c o n t r a a s componentes f o r t e m e n t e
56
57
∗ c o n e x a s do g r a f o . E s t a s s a o armazenadas no v e t o r s c c
58
∗ que pode s e r a c e s s a d o p e l o metodo g e t _ s c c _ a r r a y ( ) .
∗/
v o i d strongly_connec te d_c om po ne nts _a lg o r it hm ( ) ;
59
60
61
/∗ Encontra um caminho de x a y . R etorna t r u e s e achou caminho .
62
b o o l find_path ( i n t x , i n t y ) ;
63
};
64
65
66
#e n d i f
codigo/search.h
1
#i f n d e f DFS_CPP_
2
#d e f i n e DFS_CPP_
3
4
#i n c l u d e " s e a r c h . h "
5
6
u s i n g namespace s t d ;
7
8
i n t const ∗ Search : : get_scc_array ( ) {
r et u r n ( i n t const ∗) scc ;
9
10
}
11
12
i n t c o n s t ∗ S e a r c h : : get_parent_array ( ) {
r et u r n ( i n t const ∗) parent ;
13
14
}
15
16
v o i d S e a r c h : : strongly_conne ct ed_c o mpo ne nts _a l g o ri thm ( ) {
17
Digraph ∗H = new Digraph (G) ;
18
H−>t r a n s p o s e ( ) ;
19
∗/
117
20
S e a r c h S (H) ;
21
S . dfs () ;
22
dfs (S . vertices_sorted_by_finish_time ) ;
23
24
d e l e t e H;
25
26
}
27
28
S e a r c h : : S e a r c h ( Digraph ∗G) {
29
t h i s −>G = G;
30
n = G−>get_n ( ) ;
31
32
s c c = new i n t [ n ] ;
33
p a r e n t = new i n t [ n ] ;
34
}
35
36
Search : : ~ Search ( ) {
37
delete
[ ] parent ;
38
delete
[ ] scc ;
39
}
40
41
void Search : : d fs ( ) {
reset () ;
42
43
f o r ( i n t u = 0 ; u < n ; u ++)
44
45
i f ( p a r e n t [ u ] == NOONE) {
46
component_counter ++;
parent [ u ] = u ;
47
v i s i t (u) ;
48
}
49
50
}
51
52
v o i d S e a r c h : : d f s ( l i s t <i n t > &o r d e r ) {
Capítulo 9. Anexo
118
reset () ;
53
54
f o r ( l i s t <i n t > : : i t e r a t o r u = o r d e r . b e g i n ( ) ; u != o r d e r . end ( ) ; u ++)
55
i f ( p a r e n t [ ∗ u ] == NOONE) {
56
component_counter ++;
57
58
p a r e n t [ ∗ u ] = ∗u ;
59
v i s i t (∗u) ;
}
60
61
}
62
63
void Search : : v i s i t ( i n t u ) {
l i s t <i n t > &n e i g h b o r s = G−>a d j [ u ] ;
64
65
66
s c c [ u ] = component_counter ;
67
f o r ( l i s t <i n t > : : i t e r a t o r v = n e i g h b o r s . b e g i n ( ) ; v != n e i g h b o r s . end
( ) ; v ++) {
i f ( p a r e n t [ ∗ v ] == NOONE) {
68
69
parent [ ∗ v ] = u ;
70
v i s i t (∗ v) ;
}
71
}
72
73
v e r t i c e s _ s o r t e d _ b y _ f i n i s h _ t i m e . push_front ( u ) ;
74
75
}
76
77
78
void Search : : r e s e t ( ) {
f o r ( i n t i = 0 ; i < n ; i ++) {
79
p a r e n t [ i ] = NOONE;
80
s c c [ i ] = NOONE;
81
}
82
83
component_counter = 0 ;
84
vertices_sorted_by_finish_time . c l e a r ( ) ;
119
85
}
86
87
b o o l S e a r c h : : find_path ( i n t x , i n t y ) {
reset () ;
88
89
90
parent [ x ] = x ;
91
r e t u r n visit_u_look_fo r _v ( x , y ) ;
92
}
93
94
b o o l S e a r c h : : visit_u_look_f o r_v ( i n t u , i n t v ) {
i f ( u == v )
95
return true ;
96
97
l i s t <i n t > &n e i g h b o r s = G−>a d j [ u ] ;
98
99
f o r ( l i s t <i n t > : : i t e r a t o r z = n e i g h b o r s . b e g i n ( ) ; z != n e i g h b o r s . end
100
( ) ; z ++) {
i f ( p a r e n t [ ∗ z ] == NOONE) {
101
102
parent [ ∗ z ] = u ;
103
i f ( visit_u_look_f o r_v ( ∗ z , v ) )
104
return true ;
105
}
}
106
107
return f a l s e ;
108
109
}
110
111
#e n d i f
codigo/search.cpp
1
#pragma once
2
#i f n d e f SIMULATION_H
3
#d e f i n e SIMULATION_H
Capítulo 9. Anexo
120
4
5
#i n c l u d e " d i g r a p h . h "
6
#i n c l u d e " p a r t i t i o n . h "
7
8
9
10
c l a s s Simulation {
public :
11
S i m u l a t i o n ( Digraph ∗G, i n t s e e d ) ;
12
v i r t u a l ~ Simulation () ;
13
Partition ∗ get_partition () ;
14
15
16
private :
17
Digraph ∗ graph ;
18
Partition ∗ partition ;
19
in t seed ;
i n t n , n_squared ;
20
21
i n t l a b e l _ f u n c t i o n ( m u l t i s e t <i n t >) ;
22
23
};
24
25
#e n d i f
/∗ SIMULATION_H ∗/
codigo/simulation.h
1
#i n c l u d e <s e t >
2
#i n c l u d e " s i m u l a t i o n . h "
3
4
5
i n t S i m u l a t i o n : : l a b e l _ f u n c t i o n ( m u l t i s e t <i n t > M) {
i n t sum = 0 ;
6
7
8
9
f o r ( m u l t i s e t <i n t > : : i t e r a t o r i = M. b e g i n ( ) ; i != M. end ( ) ; i ++)
sum += ∗ i ;
121
sum %= n_squared ;
10
11
r e t u r n sum ;
12
13
}
14
15
S i m u l a t i o n : : S i m u l a t i o n ( Digraph ∗G, i n t s ) {
16
graph = G;
17
seed = s ;
18
n = G−>get_n ( ) ;
19
n_squared = n ∗ n ;
20
21
i n t ∗ o l d _ l a b e l = new i n t [ n ] , ∗ l a b e l = new i n t [ n ] ;
22
23
// I n i c i a l i z a t o d o s o s r o t u l o s com 0 e o r o t u l o de ’ s e e d ’ com 1
24
f o r ( i n t i = 0 ; i < n ; i ++)
25
26
old_label [ i ] = 0;
old_label [ seed ] = 1;
27
28
// C r i a uma p a r t i c a o ordenada u n i t a r i a contendo nÃºmeros de 1 a n
29
P a r t i t i o n ∗P = new P a r t i t i o n ( n ) ;
30
31
// R e f i n a a p a r t i c a o ordenada P de a c o r d o com o s r o t u l o s
32
P−>r e f i n e _ o r d e r e d _ p a r t i t i o n _ u s i n g _ l a b e l s ( o l d _ l a b e l ) ;
iniciais
33
34
f o r ( bool s t a b i l i z e d = f a l s e ; ! s t a b i l i z e d ; ) {
35
st a bi li zed = true ;
36
f o r ( i n t i = 0 ; i < n ; i ++) {
37
m u l t i s e t <i n t > n e i g h b o r h o o d ;
38
neighborhood . i n s e r t ( old _ lab el [ i ] ) ;
39
l i s t <i n t > &n e i g h b o r s = G−>a d j [ i ] ;
40
41
f o r ( l i s t <i n t > : : i t e r a t o r j = n e i g h b o r s . b e g i n ( ) ; j !=
n e i g h b o r s . end ( ) ; j ++)
Capítulo 9. Anexo
122
neighborhood . i n s e r t ( old _ lab el [ ∗ j ] ) ;
42
l a b e l [ i ] = lab el_ fu n ct ion ( neighborhood ) ;
43
}
44
45
46
// R e f i n a a p a r t i c a o ordenada P de a c o r d o com o s novos r o t u l o s
47
s t a b i l i z e d = ! ( P−>r e f i n e _ o r d e r e d _ p a r t i t i o n _ u s i n g _ l a b e l s ( l a b e l ) )
;
48
49
i n t ∗tmp = o l d _ l a b e l ;
50
old_label = label ;
51
l a b e l = tmp ;
}
52
53
54
delete
[ ] old_label ;
55
delete
[ ] label ;
56
p a r t i t i o n = P;
57
58
}
59
60
61
Simulation : : ~ Simulation () {
/∗ Ver porque e s t a assim , e pq e ’ v i r t u a l ’ . . . ∗/
62
63
}
64
65
Partition ∗ Simulation : : get_partition () {
return partition ;
66
67
}
codigo/simulation.cpp
Download
Título do Projeto - Pós-Graduação em Ciência da Computação

Título do Projeto - Pós-Graduação em Ciência da Computação

Idéias Iniciais

02 Algoritmos

Fila

GRAFOS - Ensino de Matemática

Grafos: fluxos e árvores de expansão

COS242 * Teoria dos Grafos 1º Trabalho Prático

Mapeamento e Localização para Robótica Móvel Nathaly

grafos_notas_de_aula_parte1

ANALISE SOCIO-ECONOMICA DAS SENTENÇAS

Fluxo Maximo e Emparelhamento
