TABELA DE FERRAMENTAS “GEOGEBRA 4”
JANELA 1
JANELA 2
JANELA 3
JANELA 4
JANELA 5
JANELA 6
JANELA 7
JANELA 8
JANELA 9
JANELA 10
JANELA 11
JANELA 12
Mover
Novo Ponto
Reta definida
Reta
Polígono
Círculo
Elipse
Ângulo
Reflexão com
Inserir Texto
Seletor
Deslocar Eixos
por dois
Perpendicular
Incluir Imagem
Caixa para
Ampliar
pontos
definido pelo
relação a uma
centro e um
reta
dos seus
pontos
Girar em
Ponto em objeto
Segmento
torno de um
definido por
ponto
dois pontos
Reta Paralela
Polígono Regular
Círculo dados
Hipérbole
centro e raio
relação a um
Exibir/Esconder
ponto
Objetos
Segmento com
Planilha de
ponto
comprimento
comprimento
fixo
ou perímetro
Intersecção entre dois
Semirreta
objetos
definida por
Bissetriz
dois pontos
Parábola
amplitude fixa
Vincular/Desvincular
Polígono Rígido
Compasso
Reflexão com
Gravar para a
Cálculo
Mediatriz
Ângulo com
Distância,
Área
Inversão
Caneta
Inserir botão
Reduzir
Girar em
Relação entre
Inserir Campo de
Exibir/Esconder
dois Objetos
Entrada
Objetos
Polígono
Círculo
Cônica
Semideformável
definido por
definida por
torno de um
três pontos
cinco pontos
ponto por um
ângulo
Ponto Médio
Tangentes
Semicírculo
Inclinação
Transladar
Exibir/Esconder
1
Número Complexo
Caminho
definido por
objeto por um
Calculadora de
poligonal
dois pontos
vetor
probabilidade
Ampliar ou
Inspetor de
Copiar Estilo
funções
Visual
Vetor definido
Reta Polar ou
Arco circular
por dois
Diametral
dados o centro
reduzir
e dois pontos
objetos dados
pontos
Criar lista
Rótulo
centro e fator
de homotetia
Vetor a partir
Reta de
Arco
de um ponto
Regressão
circuncircular
Linear
dados três
Apagar Objeto
pontos
Lugar
Setor circular
Geométrico
dados o centro
e dois pontos
Setor
circuncircular
dados três
pontos
2
ATALHOS
Shift
Seleciona a opção Mover
Atualiza
desenho. Apaga o “Rastro” deixado por um objeto
Nova Janela
Mostrar/Esconder Janela de
Álgebra
Abrir Arquivo
Salvar Arquivo
Ativa a opção
Seleciona vários objetos
Desfazer uma ação
Zoom
1
ENTRADA DE COMANDOS
O Campo de Entrada fica no rodapé da Zona Gráfica do GeoGebra. Através deste campo, é
possível operar com o GeoGebra, usando comandos escritos. Praticamente todas as ferramentas da
Barra de Ferramentas podem ser usadas usando os comandos escritos.
3
Vale ressaltar que existem comandos acessíveis no CAMPO DE ENTRADA e que não estão
na Barra de Ferramentas. Como exemplo, sugerimos que digite no CAMPO DE ENTRADA e
pressione ENTER.

A = (1, 3)

B = (3, 4)

Elipse [A, B, 2]
Observamos que os dois primeiros comandos geram pontos, assim como a ferramenta
NOVO PONTO (Janela 1). A diferença é que pela referida ferramenta o ponto é obtido através de
um clique com mouse e perde em precisão (nas coordenadas cartesianas). No Campo de Entrada,
podemos dizer EXATAMENTE onde o ponto aparecerá. O último comando está disponível
também através da Barra de Ferramentas,
(Janela 7). Basta clicar sobre este botão e depois
sobre os pontos A e B e em um terceiro ponto por onde a elipse passará.
Não iremos mostrar todas as ferramentas disponíveis nesta janela, mas há uma maneira de ir
descobrindo-as. Comece a digitar o comando na Entrada de Comandos e você poderá perceber
que o GeoGebra completa sua palavra ou seu comando. Se é o comando desejado, clique em
ENTER e abrirá uma janela de diálogo mostrando o que é preciso para concluir o comando.
1.1 OPERADORES
No GeoGebra, assim como em qualquer software que trabalhe com matemática, os
operadores são ativados de forma bem simples. A seguir, encontra-se uma tabela com os principais
operadores e suas funções.
4
OPERADOR
FUNÇÃO
+
Operador adição: adiciona o que está à esquerda com o que está à direita.
-
Operador subtração: subtrai o que está à esquerda do que está à direita.
*
Operador multiplicação: multiplica o que está à esquerda com o que está à direita.
Obs.: o espaço também é entendido como multiplicação. Assim, escrever 2*x e 2 x,
obtém-se o mesmo resultado.
/
Operador divisão: divide o que está à esquerda com o que está à direita.
^
Operador potência: o que está à esquerda é considerado base e o que está à direita o
expoente. Por exemplo: x^2 é o mesmo que x². Alternativamente, pode-se usar
combinações AltGr + 2 e AltGr + 3 (do teclado) para gerar ² e ³. Escrevendo x² e x³, o
GeoGebra também aceita.
sqrt(...)
Operador raiz quadrada: extrai a raiz quadrada de “...”.
cbrt(...)
Operador raiz cúbica: extrai a raiz cúbica de “...”.
log(...) ou ln(...)
ld(...)
Operador logaritmo natural: calcula o logaritmo natural de “...”.
Operador de logaritmo binário: calcula o logaritmo binário de “...”, ou seja, calcula o
logaritmo de “...”, mas na base 2.
lg(...)
Operador de logaritmo decimal: calcula o logaritmo decimal de “...”, ou seja, calcula o
logaritmo de “...”, mas na base 10.
sin(...)
Operador seno: calcula seno de “...”.
Obs.: medida em radianos.
cos(...)
Operador cosseno: calcula o cosseno de “...”.
Obs.: medida em radianos.
tan(...)
Operador tangente: calcula a tangente de “...”.
Obs.: medida em radianos.
abs(...)
Operador valor absoluto: calcula o valor absoluto de “...”. Lembre-se que | | = valor
absoluto de x.
2
FOLHA DE CÁLCULO
Na Folha de Cálculo, cada célula tem um nome específico que permite identificá-la
diretamente. Por exemplo, a célula na coluna A e linha 1 é nomeada A1.
Nota: O nome de uma célula pode ser usado em expressões e em comandos para identificar o
conteúdo da célula correspondente.
Exemplo: Usando numa expressão que represente uma função afim ( )
.
5
Nas células da folha de cálculo pode inserir não só números, mas também todo tipo de
objetos matemáticos suportados pelo GeoGebra (coordenadas de pontos, funções, comandos). Se
possível, o GeoGebra mostra imediatamente na Zona Gráfica a representação gráfica do objeto
inserido numa célula. O objeto assume o nome (rótulo) da célula usada para o criar (A5, C1).
Nota: Injustificavelmente os objetos na folha de cálculo são classificados como Objetos Auxiliares
na Zona Algébrica. As funções desta folha são semelhantes ao da Planilha do Excel.
3
TABELA DE COMANDOS
Novo Ponto
A = (a, b)
Vetor
u = (a,b)
Módulo do Vetor u
n_u = comprimento[u]
Segmento de reta
s = Segmento[A,B]
Mediatriz de um segmento
m = mediatriz[s]
Ponto médio de um segmento de reta
M = pontomédio[s]
Ponto de intersecção de duas retas
I = intersecção[f,g]
Círculo/circunferência (Centro, ponto)
C_1 = círculo[A,B]
Círculo/circunferência (Centro, raio)
C_1 = círculo[A,r]
6
4
Abscissa de um ponto A
A_x = x(A)
Ordenada de um ponto A
A_y = y(A)
Equação reduzida de uma reta
r: y = m*x+b
Gráfico de uma função
f(x)...
Ponto móvel no gráfico
M = ponto[f]
Zero(s) de uma função
x_1 = raiz[f]
Extremo(s) de uma função
E_1 = extremo[f]
Gráfico de uma função num intervalo
f(x) = função[g(x), a,b]
CONSTRUÇÕES NO GEOGEBRA
4.1 FUNÇÃO DO 1º GRAU
- Insira dois seletores: (a) e (b) respectivamente, tendo eles mínimo (-10), máximo (10) e
incremento (1).
- No Campo de Entrada, digite a definição da equação do 1º Grau
( )
,
seguindo como parâmetros os seletores (a) e (b). Após dê ENTER para finalizar a construção.
- Para melhor entendimento do exercício, mova qualquer dos seletores e analise as
mudanças do gráfico da função.
Complementação da construção:
- Crie um ponto sobre o eixo das abscissas com o comando Ponto[EixoX]. Denomine este
Ponto para “P”.
- Construa uma reta perpendicular do Ponto “P” em relação ao eixo das abscissas. Denomine
esta reta de “c”.
7
- Defina a intersecção da reta “c” com a função f(x). Denomine este ponto para “A”.
- Construa uma reta perpendicular do Ponto “A” em relação ao eixo das ordenadas.
Denomine esta reta de “d”.
- Defina a intersecção da reta “d” com o eixo das ordenadas. Denomine este ponto de “P_1”.
- Esconda as retas “c” e “d”.
- Crie um segmento definido por dois pontos, do ponto “A” à “P”. Denomine este segmento
de “e”.
- Crie um segmento definido por dois pontos, do ponto “A_1” à “P”. Denomine este
segmento de “g”.
- Modifique o Estilo destes segmentos “e” e “g”. Deixe-as tracejadas.
- Edite nas Propriedades do Ponto A. Exibir Rótulo: Nome & Valor.
- Edite nas Propriedades do Ponto P. Legenda: x(A); Exibir Rótulo: Legenda.
- Edite nas Propriedades do Ponto P_1. Legenda: y(A); Exibir Rótulo: Legenda.
8
Concluiremos a construção da seguinte maneira.
Essa nova construção nos leva a novos questionamentos pertinentes:
- Quando “x(A)” for 3, qual será sua correspondente “y(A)”?
- Se substituirmos na função “f(x)” o “x” por 3, quanto será “y”?
4.1.1
DOMÍNIO E IMAGEM
Sabemos pela definição de Funções do 1° Grau que o Domínio e Imagem desta, serão todos
os Reais.
4.1.2
INTERVALOS
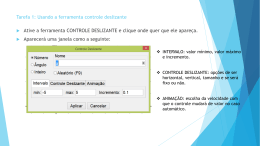
Podemos ainda, trabalhar com intervalos.
9
- Insira dois seletores: (a) e (b) respectivamente, tendo eles mínimo (-10), máximo (10) e
incremento (1).
- No Campo de Entrada, digite o comando de Função[
, -5, 5], seguindo como
parâmetros os seletores (a) e (b). Após dê ENTER para finalizar a construção.
- Para melhor entendimento do comando, digite na Entrada de Comandos Função[] e então
ENTER. Será visualizada a seguinte janela:
No caso do comando que nós atribuímos, foi Função
, valor de x inicial = -5 e
valor de x final = 5.
4.2 INEQUAÇÕES DO 1° GRAU
Sendo
um função do 1° Grau, uma inequação do 1° Grau é toda inequação
redutível a uma das formas seguintes.
Em uma inequação do 1° Grau, os valores da variável que transformam a inequação em uma
desigualdade verdadeira recebem o nome de soluções da inequação.
10
O conjunto de todas as soluções de uma inequação é o conjunto solução (S) ou conjunto
verdade desta inequação.
O processo de resolução de uma inequação do 1° Grau envolve descobrir os valores de x
para os quais
ou
ou
, o que é chamado de estudo do
sinal de uma Função do 1° Grau.
A seguir vamos construir a demonstração do conjunto solução da inequação do 1° Grau.
- Insira na Entrada de Comandos, a = -2 e ENTER.
- Insira na Entrada de Comandos, b = 1 e ENTER.
Obs.: inserindo diretamente os valores, são criados seletores na Janela de Álgebra, após a
construção é só clicar com o botão direito do mouse sobre eles na Janela de Álgebra e selecionar a
opção Exibir Objetos.
- Digite na Entrada de Comandos a expressão ( )
.
- Crie um ponto sobre o EixoX. Na Janela 2, selecione a opção
Novo Ponto (A) e então
clique com o botão esquerdo do mouse sobre o eixo das abscissas.
Obs.: Apertando ESC para selecionar a opção
Mover. Mova o ponto (A) no eixo das
abscissas. Perceba que este ponto está fixo no eixo.
- Crie uma
reta perpendicular(c) que passe pelo ponto criado no EixoX em relação ao
eixo das Abscissas.
- Marque a
intersecção da reta(c) e a reta (f(x)). Criado o ponto, denomine-o de (P).
Obs.: Apertando ESC para selecionar a opção
Mover. Mova o ponto (A) e perceba o
comportamento do ponto (P).
- Habilite o rastro do ponto (P).
11
Faça o mesmo processo da observação anterior e analise a situação.
Na inequação o conjunto solução, como já explicita no início do capítulo é o conjunto
verdade da sentença. Neste caso, gostaríamos de saber o conjunto verdade da sentença
, ou seja, o conjunto solução é
. Iremos então, representá-lo na reta o
conjunto solução. Seguiremos os passos então:
- Clique com o botão direito do mouse sobre o ponto (P) e selecione a opção Propriedades.
- Selecione a janela Avançado.
Nosso objetivo é demonstrar quais valores da minha equação torna a sentença verdadeira, ou
seja,
. Então vamos digitar na janela de diálogo de Condições para mostrar Objeto, x(A) < =
1 / 2 que neste caso seria o domínio da inequação.
12
Movimentando o ponto (A) podemos verificar a solução da minha inequação.
Para estudar outras sentenças é só mudar os parâmetros (a) e (b) da equação, no caso serão
os seletores.
4.3 CONSTRUÇÃO DE GRÁFICOS – PLANILHA DE CÁLCULO
Neste capítulo vamos trabalhar com construção de gráficos através da Planilha de Cálculo.
A Planinha tem uma interface como a Microsoft Office Excel, nos dispõe também função
semelhantes e também do Campo de Entrada do GeoGebra.
4.3.1
PONTOS
Tradicionalmente, no estudo de funções, para a construção dos gráficos os professores usam
a tabelinha. Neste caso não seria muito diferente, a vantagem seria uma abordagem eficaz e com
ferramentas dinâmicas.
Primeiramente vamos analisar como se determina elementos na grade.
Como identificado o elemento da coluna A e linha 4? Semelhante às operações feitas no
Excel, vamos identificá-lo como A4. No caso o elemento que está localizado na casa A4 é o 5.
13
Agora que sabemos identificar na planilha, iremos construir uma sequência de números na
coluna A.
- Digite na casa A1 o número -5 e dê ENTER.
- Digite na casa A2 o A1+1 e dê ENTER.
- Digite na casa A3 o A2+1 e dê ENTER.
- Repita o mesmo processo até a casa A11.
Perceba que houve uma sequência, no qual a casa sucessora era resultado da casa
antecessora + 1.
Já sabemos então como definir valores independentes de x. A seguir vamos definir os
valores dependentes de y na construção de pontos. Entendemos que os valores de y são encontrados
através de f(x).
- Na coluna B1, digite a expressão -2*(A1)+1. Note que A1 = -5.
- Na coluna B2, digite a expressão -2*(A2) +1. Note que A2 = -4.
- Repita o processo até B11.
Temos então, as coordenadas x, y dos pontos definidos pela expressão
.A
seguir, vamos construir estes pontos na Janela Gráfica. Segue o processo:
- Digite na casa C1 o seguinte: (A1, B1) e dê ENTER.
- Digite na casa C2 o seguinte: (A2, B2) e dê ENTER.
- Repita o processo até C11.
14
Perceba na Janela Gráfica os pontos criados.
Se não for possível visualizar todos os pontos, é preciso
4.3.2
Reduzir o zoom.
ESBOÇO DO GRÁFICO
Como na Entrada de Comandos, é possível inserir o comando de Função[] nas casa da
Planilha de Cálculo. Seguindo o exemplo acima, temos como intervalos reais da função [-5, 5] e a
expressão
. Logo o Comando será Função
- Digite na casa A13 o comando Função
.
e dê ENTER.
15
4.4 DEMONSTRAÇÕES
4.4.1
TRIÂNGULOS
Considerando três pontos não colineares A, B e C, podemos dizer que a união dos três
segmentos ̅̅̅̅, ̅̅̅̅ e ̅̅̅̅ , recebe é chamado de Triângulo. São classificados pela medida de seus
lados ou ainda pelos seus respectivos ângulos internos.
4.4.1.1 CONDIÇÃO DE EXISTÊNCIA DE UM TRIÂNGULO
Para que possa ser construído um triângulo é necessário que a medida de qualquer um dos
lados seja menos que a soma das medidas dos outros dois e maior que o valor absoluto da diferença
entre essas medidas.
|
|
1º Exemplo: Triângulo de lados 2, 3 e 4 cm.
- Construa um
segmento com comprimento fixo na Janela Gráfica. Irá abrir uma janela
de diálogo pedindo o comprimento do segmento, digite 2.
16
- Construa um
círculo dados centro e raio. Primeiro clique sobre o ponto A, pertencente
a um dos extremos do segmento já criado, então digite na janela de diálogo a medida do outro lado
do triângulo, neste caso será 3.
- Construa outro
círculo dados centro e raio. Primeiro clique sobre o ponto B,
pertencente ao outro extremo do segmento já criado, então digite na janela de diálogo a medida do
terceiro lado do triângulo, neste caso 4.
- Defina a
intersecção destas duas circunferências. Denomine-o este ponto de C.
- Construa um
segmento ̅̅̅̅ .
- Construa um
segmento ̅̅̅̅ .
2º Exemplo: Triângulo de lados 1, 1 e 3.
Construa um
segmento com comprimento fixo na Janela Gráfica. Irá abrir uma janela
de diálogo pedindo o comprimento do segmento, digite 1.
17
- Construa um
círculo dados centro e raio. Primeiro clique sobre o ponto A, pertencente
a um dos extremos do segmento já criado, então digite na janela de diálogo a medida do outro lado
do triângulo, neste caso será 1.
- Construa outro
círculo dados centro e raio. Primeiro clique sobre o ponto B,
pertencente ao outro extremo do segmento já criado, então digite na janela de diálogo a medida do
terceiro lado do triângulo, neste caso 3.
- Defina a
intersecção destas duas circunferências. (Impossível)
4.4.1.2 CLASSIFICAÇÃO DOS TRIÂNGULOS
a) Triângulo Equilátero: três lados congruentes (medidas iguais); três ângulos internos
congruentes (iguais) de 60º, sendo assim classificado como polígono regular.
Exemplo 1: Triângulo de lados 2, 2 e 2cm.
- Construa um
segmento de comprimento fixo igual a 2.
- Construa um
círculo dados centro (A) e raio igual a 2.
- Construa outro
- Define a
círculo dados centro (B) e raio igual a 2.
intersecção entre as duas circunferências. Denomine-o este ponto de C.
- Construa um
segmento ̅̅̅̅ .
- Construa um
segmento ̅̅̅̅ .
- Define o
ângulo entre os pontos
̂ .
Obs.: normalmente para se obter o ângulo interno, deve-se seguir a sequência no sentido
anti-horário em relação ao centro.
- Define o
ângulo entre os pontos
̂ .
- Define o
ângulo entre os pontos
̂ .
18
Ilustração do Exemplo 1.
b) Triângulo Isósceles: dois lados congruentes; dois ângulos internos congruentes e o terceiro
ângulo formado pelos lados congruentes é chamado de ângulo do vértice.
Exemplo 2: Triângulo de lados 2, 2 e 1cm.
- Construa um
segmento de comprimento fixo igual a 1.
- Construa um
círculo dados centro (A) e raio igual a 2.
- Construa outro
círculo dados centro (B) e raio igual a 2.
- Determine a
intersecção entre as duas circunferências.
- Construa um
segmento ̅̅̅̅ .
- Construa um
segmento ̅̅̅̅ .
- Define o
ângulo entre os pontos
̂ .
- Define o
ângulo entre os pontos
̂ .
- Define o
ângulo entre os pontos
̂ .
19
Ilustração do Exemplo 2.
c) Triângulo Escaleno: a medida dos três lados diferentes. Ângulos internos diferentes.
Exemplo 3: Triângulo de lados 3, 4 e 5 cm.
- Construa um
segmento de comprimento fixo igual a 5.
- Construa um
círculo dados centro (A) e raio igual a 3.
- Construa outro
círculo dados centro (B) e raio igual a 4.
- Determine a
intersecção entre as duas circunferências.
- Construa um
segmento ̅̅̅̅ .
- Construa um
segmento ̅̅̅̅ .
- Define o
ângulo entre os pontos
̂ .
- Define o
ângulo entre os pontos
̂ .
- Define o
ângulo entre os pontos
̂ .
20
Ilustração do Exemplo 3.
d) Triângulo Retângulo: possui um dos ângulos internos, reto (90º graus).
Exemplo 3.
e) Triângulo Obtusângulo: possui um dos três ângulos interno obtuso (maior que 90º graus).
Seguindo os mesmos processos de construção, mas com medidas diferentes nos lados,
encontramos o triângulo obtusângulo.
Ilustração do Triângulo Obtusângulo no GeoGebra.
a) Triângulo acutângulo: possui os três ângulos internos menores que 90º graus.
Exemplo 1.
4.4.2
ÁREA DO TRIÂNGULO
- Esconda a Malha.
- Digite na Entrada de Comandos A = (0,0) e dê ENTER.
- Digite na Entrada de Comandos B = (0,4) e dê ENTER.
21
- Digite na Entrada de Comandos C = (1,2) e dê ENTER.
- Encontre o
ponto médio dos pontos C e B. Denomine-o de M.
- Construa uma
reta passando por A e B. Denomine-a de a.
- Construa uma
reta perpendicular a reta a e que passe pelo ponto C. Denomine-a de b.
-
Esconda os Eixos.
- Defina a
-
intersecção da reta b e da reta a. Denomine este ponto de H.
Esconda a reta b.
segmento ̅̅̅̅. Edite este segmento em Propriedades/Estilo/Estilo da
- Construa um
Linha e escolha a forma tracejada. Também
-
Esconda seu Rótulo.
Esconda a reta a.
- Construa o
Polígono ABC.
Obs.: Para construir polígonos quaisquer, devem-se selecionar os vértices do polígono e
fechá-lo sempre no primeiro ponto selecionado, ou seja, o primeiro vértice será o último também.
- Crie na Janela Gráfica um Seletor de mínimo = 0, máximo = 1 e incremento = 0.1.
Denomine-o de t.
- Digite na Entrada de Comandos
- Com a ferramenta
Girar em torno de um ponto por um ângulo, será criado um ponto
que gire em torno do ponto M pelo ângulo
ponto M e então defina o ângulo
e dê ENTER.
. Primeiro selecione o ponto A, o centro que será o
e escolha a opção sentido horário como na ilustração abaixo e dê
OK. Será criado o ponto A .
- Agora faremos o mesmo processo, mas agora selecione primeiro o ponto C, o centro será o
ponto M e o ângulo . Opção sentido horário e OK.
22
- Agora faremos o mesmo processo, mas agora selecione primeiro o ponto B, o centro será o
ponto M e o ângulo . Opção sentido horário e OK.
Polígono A B C . Caso não consiga visualizar os pontos ou não selecioná-
- Construa o
los, movimente o seletor para movimentar os pontos.
- Defina o
4.4.3
ângulo
̂ .
- Construa o
segmento definido por dois pontos ̅̅̅̅ .
- Construa o
segmento definido por dois pontos ̅̅̅̅ .
CICLO TRIGONOMÉTRICO
- Esconda a Malha.
- Defina a
intersecção do eixo das abscissas e do eixo das ordenadas. Denomine-a de C.
- Construa um
círculo dados centro e raio. O centro será o ponto C e raio = 1.
Denomine-a de “c”.
- Construa um
novo ponto na coordenada (1,0). Denomine-o de A.
- Construa um
novo ponto sobre a circunferência c. Denomine-o de P.
- Construa uma
reta definida por dois pontos. Selecione primeiro o ponto C e depois P.
Denomine-a de a.
- Construa uma
reta perpendicular em relação ao eixo das ordenadas e que passe pelo
ponto P. Denomine-a de b.
- Defina a
intersecção da reta b e o eixo das ordenadas. Denomine-o de S.
- Construa um
segmento definido por dois pontos. Selecione primeiro o ponto C e
depois S. Denomine-o de d.
- Construa um
segmento definido por dois pontos. Selecione primeiro o ponto P e
depois S. Denomine-o de b_1.
- Construa uma
reta perpendicular em relação ao eixo das abscissas e que passe pelo
ponto P. Denomine-a de e.
- Defina a
intersecção da reta e e o eixo das abscissas. Denomine-o de S_1.
- Construa um
segmento definido por dois pontos. Selecione primeiro o ponto C e
depois S_1. Denomine-o de d_1.
23
- Construa um
segmento definido por dois pontos. Selecione primeiro o ponto P e
depois S_1. Denomine-o de e_1.
- Defina o
ângulo de
- Construa uma
̂ . Na sequência, primeiro A, C e depois P.
reta paralela ao eixo das ordenadas e que passe pelo ponto A.
Denomine-a de f.
- Defina a
intersecção entre a reta f e a reta a. Denomine-o de T.
- Construa um
segmento definido por dois pontos. Selecione primeiro o ponto A e
depois T. Denomine-o de f_1.
- Arraste a ferramenta
Mover na construção, como se fosse uma seleção de arquivos.
Clique com o botão direito do mouse. Selecione a opção
Esconder Rótulo. Fará que limpe a
Zona Gráfica.
- Modifique as propriedades dos segmentos d, f_1 e d_1. Mude a cor destes, uma diferente
da outra.
- Modifique as propriedades dos segmentos e_1 e b_1. Mude o estilo da linha para tracejada
e de cor cinza.
-
Esconda os Objetos e, f, e b.
- Selecione o ponto S_1, em propriedades/básico escolha a opção Exibir Rótulo e então
Valor.
- Faça o mesmo com os pontos S_1 e T.
24
Ciclo Trigonométrico
4.4.4
ÁREA DO TRAPÉZIO
- Construa uma
- Construa um
- Construa uma
- Construa um
reta definida por dois pontos. Denomine-a de a e os pontos de A e B.
novo ponto não pertencente a esta reta. Denomine-o de C.
reta paralela a reta a que passe pelo ponto C. Denomine-a de b.
novo ponto sobre a reta b. Denomine-o de D.
- Defina o
ponto médio entre os pontos A e C. Denomine-o de E.
- Defina o
ponto médio entre os pontos B e D. Denomine-o de F.
- Construa um
polígono dos pontos A, B, C e D. Denomine-o de ABCD e seus
segmentos de c_1, c_2, c_3 e c_4.
- Construa um
seletor de ângulo mínimo = 0º e máximo = 180º. Denomine-o de t.
- Defina Condição para mostrar os Objetos ABCD, c_1, c_2, c_3 e c_4 para t = 0°.
25
Dica: o símbolo de graus não pode ser digitado pelo teclado, deve ser selecionado janela de
símbolos no canto.
- Com a ferramenta
girar em torno de um ponto por um ângulo, será criado um ponto
que gire em torno do ponto F pelo ângulo
definido pelo seletor. Primeiro selecione o ponto E, o
centro que será o ponto F e então defina o ângulo
e escolha a opção sentido horário como na
ilustração abaixo e dê OK. Será criado o ponto E .
- Faça o mesmo com os pontos C e D. Serão criados os pontos C e D .
- Construa um
polígono dos pontos A, B, E e F. Denomine-o de ABEF e seus
segmentos de d_1, d_2, d_3 e d_4.
- Construa um
polígono dos pontos E , F, D e C . Denomine-o de E FD C e seus
segmentos e_1, e_2, e_3 e e_4.
- Defina Condições para mostrar os Objetos E FD C , e_1, e_2, e_3 e e_4 para t > 0º.
- Defina Condições para mostrar os Objetos ABEF, d_1, d_2, d_3 e d_4 para t > 0º.
- Defina Condições para mostrar os Objetos E, F, E , C e D para t > 0º.
- Selecione todos os Objetos e
- Construa uma
- Defina a
esconda seus Rótulos.
reta perpendicular a reta a e que passe por C. Denomine-a de f.
intersecção entre a reta f e a. Denomine o ponto de H.
- Esconda os Objetos a, b e f.
- Crie um
segmento definido pelos pontos C e D. Denomine-o de g_1.
- Crie um
segmento definido pelos pontos A e B. Denomine-o de g_2.
- Crie um
segmento definido pelos pontos A e C. Denomine-o de g_3.
- Crie um
segmento definido pelos pontos B e D. Denomine-o de g_4.
- Crie um
segmento definido pelos pontos C e H. Denomine-o de h.
- Crie um
segmento definido pelos pontos A e H. Denomine-o de g_5.
- Modifique as propriedades/estilo/estilo das linhas g_1, g_2, g_3, g_4 e g_5 para
pontilhada e desmarque Exibir Rótulo.
26
- Modifique as propriedades/estilo/estilo da linha h para tracejada.
- Modifique nas propriedades/estilo/preenchimento dos polígonos ABCD, ABFE, E FD C e
arraste até 100.
- Defina o ponto médio do segmento h. Denomine-o de M.
Área do Trapézio.
5
ATIVIDADES PARA O ENSINO FUNDAMENTAL
- Construção de uma Casa com as formas geométricas conhecidas: Quadrado, retângulo,
triângulo, paralelogramo. Poderão ser trabalhadas as formas geométricas, perímetro, área de
superfícies planas.
- Teorema de Tales.
- Pontos notáveis do triângulo: Medianas e baricentro; Bissetrizes e incentro; Alturas e
ortocentro; Mediatrizes e circuncentro.
- Congruência de Triângulos: Casos de Congruência (LAL, ALA, LLL, LAAo, triângulos
retângulos).
6
ATIVIDADES PARA O ENSINO MÉDIO
- Teorema de Pitágoras.
- Função Quadrática.
- Função Exponencial.
- Funções Trigonométricas.
- Trigonometria no Triângulo Retângulo.
27
6.1.1
PROGRESSÕES GEOMÉTRICAS
- Crie um
seletor, denominado n de mínimo = 1, máximo = 6 e incremento = 1.
- Digite na Entrada de Comandos: Segmento[(n - 1, 0), (n - 1, 2^(n - 1))]
- Digite na Entrada de Comandos: Sequência[Segmento[(n - 1, 0), (n - 1, 2^(n - 1))], n, 1, 6]
-
Insira um Texto na Janela Gráfica, nesta janela vamos digitar as fórmulas da P.G.

Termo Geral: a_n = a_0 * q^{n-1}

Soma dos Termos: S_n = \frac{ a_0*(q^n - 1) }{q -1 }

Razão: q = \frac{ a_n }{a_{n-1} }
- Modifique as propriedades dos objetos para que fique mais destacados.
Representação de uma sequência geométrica.
6.1.2
PROGRESSÕES ARITMÉTICAS
- Crie um
seletor, denominado n de mínimo = 1, máximo = 6 e incremento = 1.
- Digite na Entrada de Comandos: Segmento[(n - 1, 0), (n - 1, 2 (n - 1))]
- Digite na Entrada de Comandos: Sequência[Segmento[(n - 1, 0), (n - 1, 2 (n - 1))], n, 1, 6]
-
Insira um Texto na Janela Gráfica, nesta janela vamos digitar as fórmulas da P.A.
o Termo Geral: a_n = a_1+(n-1)*r
o Soma dos Termos: S_n = n* \frac{ a_1 + a_n }{2 }
o Razão: r = a_n - a_{n-1}
- Modifique as propriedades dos objetos para que fique mais destacado.
28
Representação de uma sequência aritmética.
6.1.3
MATRIZES
Criar Matrizes:
Exemplo: Digite na Entrada de Comandos. M = {{1, 2}, {3, 4}} e ENTER. Observe a Matriz
criada na Zona Algébrica.
Definir a Matriz inversa: Digite na Entrada de Comandos, M_{-1} = MatrizInversa[M] e
ENTER.
Definir a Matriz identidade: Digite na Entrada de Comandos, I = M*M_{-1} e ENTER.
Definir a Matriz transposta: Digite na Entrada de Comandos, M_t = MatrizTransposta[M]
e ENTER.
Definir a Determinante da Matriz: Digite na Entrada de Comandos, detM =
Determinante[M] e ENTER.
Inserir a Matriz na Zona Gráfica: Digite na Entrada de Comandos, TabelaDeTexto[M] e
ENTER. Observe que não os delimitadores (parênteses) da Matriz.
Há uma segunda maneira de inserir Matriz na Zona Gráfica. Selecione a ferramenta
Inserir Texto e clique sobre na Zona Gráfica, selecione a opção fórmula LaTeX e escolha a opção
Objetos: selecione M.
29
A terceira maneira é selecionando a flecha ao lado da opção Fórmula Latex, após na opção
Matrizes e então selecionar uma das opções disponíveis na janela – Matriz 1 x 3, 3 x 1, 2 x 2 ou
ainda 3 x 3.
Secionada a matriz desejada, irá abrir esta expressão na janela de texto. Nas letras a, b, c e
d, substitua-os por 1, 2, 3 e 4 respectivamente, e clique em OK.
30
Matrizes Dinâmicas
- Crie quatro
seletores, seletor a, b, c e d.
- Digite na Entrada de Comandos, M = {{a, b},{c, d}} e ENTER.
- Selecione a ferramenta
Inserir Texto e clique sobre na Zona Gráfica, selecione a opção
fórmula LaTeX e escolha a opção Objetos: selecione M.
Manipule os seletores e analise a variação dos elementos da Matriz.
31
7
REFERÊNCIAS BIBLIOGRÁFICAS
HOHENWARTER, Markus. GeoGebra. Disponível em: <www.geogebra.org>. Acessado em: 25
Out de 2011.
AQUINO,
L.
C.
M.
Mini
curso
do
GeoGebra.
Disponível
em:
<http://www.youtube.com/watch?v=9orPBR1TXo&feature=results_main&playnext=1&list=PL8884F539CF7C4DE3>.Acessado em: 26
Out de 2011.
32
Sumário
TABELA DE FERRAMENTAS..............................................................................................1
ATALHOS................................................................................................................................3
1
ENTRADA DE COMANDOS .......................................................................................... 3
1.1
OPERADORES .......................................................................................................... 4
2
FOLHA DE CÁLCULO .................................................................................................... 5
3
TABELA DE COMANDOS ............................................................................................. 6
4
CONSTRUÇÕES NO GEOGEBRA ................................................................................. 7
4.1
FUNÇÃO DO 1º GRAU ............................................................................................ 7
4.1.1 DOMÍNIO E IMAGEM ....................................................................................... 9
4.1.2 INTERVALOS ..................................................................................................... 9
4.2
INEQUAÇÕES DO 1° GRAU ................................................................................. 10
4.3
CONSTRUÇÃO DE GRÁFICOS – PLANILHA DE CÁLCULO ......................... 13
4.3.1 PONTOS............................................................................................................. 13
4.3.2 ESBOÇO DO GRÁFICO ................................................................................... 15
4.4
DEMONSTRAÇÕES ............................................................................................... 16
4.4.1 TRIÂNGULOS ................................................................................................... 16
4.4.2 ÁREA DO TRIÂNGULO .................................................................................. 21
4.4.3 CICLO TRIGONOMÉTRICO ........................................................................... 23
4.4.4 ÁREA DO TRAPÉZIO ...................................................................................... 25
5
ATIVIDADES PARA O ENSINO FUNDAMENTAL .................................................. 27
6
ATIVIDADES PARA O ENSINO MÉDIO .................................................................... 27
6.1.1 PROGRESSÕES GEOMÉTRICAS ................................................................... 28
6.1.2 PROGRESSÕES ARITMÉTICAS .................................................................... 28
6.1.3 MATRIZES ........................................................................................................ 29
7
REFERÊNCIAS BIBLIOGRÁFICAS ............................................................................ 32
33