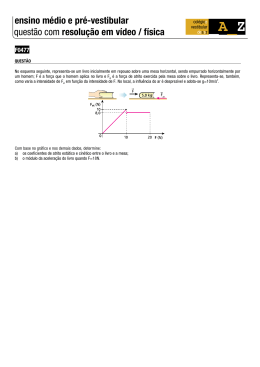
Física
2° ano
Gabarito – Prova Mensal
Thiago
Mai/09
1.
a) (UFSM - Modificada)
O bloco da figura está em repouso sobre um plano horizontal e perfeitamente liso.
A partir do instante t = 0 s, passa a atuar sobre o bloco uma força constante de
módulo igual a 15 N, e esse bloco atinge a velocidade de 20 m/s no instante t = 4 s.
Determine
a
massa
do
bloco,
em
kg.
b) (UFC - Modificada) O bloco mostrado na figura está em repouso sob a ação da
força horizontal 1, de módulo igual a 10 N, e da força de atrito entre o bloco e a
superfície. Se outra força horizontal
2,
de módulo igual a 2 N e sentido contrário,
for aplicada ao bloco, qual será a força resultante sobre ele? Justifique sua
resposta.
2.
(Fatec - Modificada) Na figura a seguir, fios e polias são ideais. O objeto A de
massa 10 kg desce com aceleração constante de 2,5 m/s2, passando pelo ponto P
com velocidade de 2 m/s.
Adotando g = 10 m/s2 e desprezando todas as forças de resistência, determine a
massa do objeto B e a velocidade com que o corpo A passa pelo ponto S.
3.
(Mackenzie - Modificada)
Um operário da construção civil necessita arrastar um bloco de concreto ao longo
de uma prancha inclinada de 30° com a horizontal. Com o objetivo de evitar o
rompimento da corda, ele foi orientado a puxar o corpo com velocidade constante,
de forma que se deslocasse 1,00 m a cada 4,0 s. Seguindo essas orientações, sabiase que a intensidade da força tensora no fio corresponderia a 57% do módulo do
peso do corpo. Considerando a corda e a polia como sendo ideais, calcule o valor
aproximado do coeficiente de atrito dinâmico entre as superfícies em contato.
4.
a) Devido à resistência do ar, as gotas de chuva caem com velocidade constante a
partir de certa altura. O módulo da força resistiva do ar é dado por F = Av2, onde
A
é
uma
constante
de
valor
8 · 10 ­6 Ns2/m2 e v é o módulo da velocidade. Nessas circunstâncias, calcule a
velocidade, em m/s, de uma gota cujo módulo do peso vale 3,2 · 10­7 N ao atingir o
solo.
b) (Uerj) Um passageiro está no interior de um elevador que desce verticalmente,
com aceleração constante "a". Se "a" vale 1/5 da aceleração da gravidade, calcule
a razão entre a intensidade da força que o piso do elevador exerce sobre o
passageiro e o peso do passageiro.
5.
(UFU - Modificada) Um bloco de massa M = 8 kg encontra-se apoiado em um
plano inclinado e conectado a um bloco de massa m por meio de polias, conforme
figura a seguir.
Dados: sen 30° = 1/2
cos 30° =
O sistema encontra-se em equilíbrio estático, e o plano inclinado está fixo no solo.
As polias são ideais e os fios, de massa desprezível. Considerando g = 10 m/s2,  =
30° e que não há atrito entre o plano inclinado e o bloco de massa M, calcule o
valor da massa m, em kg. Considere
= 1,7.
Gabarito – Prova mensal – Física 2º Ano
1. a) A aceleração do bloco pode ser calculada por:
v
20
a
a
 a  5 m / s2
t
4
Pela segunda lei de Newton, temos:
F  m  a  15  m  5  m  3 kg

b)Na situação inicial (sem a presença da força F2 ) o bloco está em repouso.

Então a força F1 não é capaz de superar a força de atrito estático máxima. Neste
caso:

FR(1)  0  F1  fat((e1))

Quando entra em ação a força F2 de intensidade 2 N, ela não é capaz de vencer



F1 . O único efeito de F2 é reduzir a força de atrito que equilibrava F1 . A força
resultante da segunda situação continua sendo nula, temos:

FR( 2 )  0  F1  fat ((e2))  F2
Comparando as duas equações, sabemos que:
fat((e1))  fat((e2))
2. Utilizando a segunda lei de Newton para os blocos A e B, temos:
 PA  T  m A  a
 PA  PB  (m A  mB )  a  100  10  mB  (10  mB )  2,5 

T  PB  mB  a
 mB  6 kg
Para determinar a velocidade do corpo A no ponto S, utilizamos a equação de
Torricelli:
VP2  VS2  2  a  S  VP2  2 2  2  2,5  28  VP  12 m / s
3. Sabendo que o bloco sobe em movimento uniforme, temos:
FR  0  T  fat  Pt  0  0,57  P    N  P  sen30º 
 0,57  P    PN  P  sen30º  0,57  P    P  cos 30º  P  sen30º 
 0,57    0,87  0,50   
7
 0,08
87
4. a) A velocidade com que a gota chega ao solo é a velocidade limite, atingida no
instante em que a força de resistência do ar equilibra-se com a força peso:
FR  0  Rar  P  A  v 2  P  8 10 2  v 2  3,2 10 7  v  2 10 3 m / s
b) Utilizando a segunda lei de Newton:
g
P
N 4
P  N  m  a  P  N  m   P   N    0,8
5
5
P 5
5. Pela condição de equilíbrio no bloco de massa M:
T  Pt  T  m  g  sen60º  T  40 3 N
Analisando as forças atuantes na polia móvel:
Portanto, pela condição de equilíbrio no bloco de massa m:
T
20 1,7
 m  g  20  3  m 10  m 
 m  3,4 kg
2
10