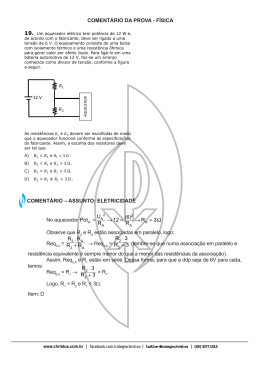
Universidade de Mogi das Cruzes – Engenharia – Curso Básico
Prof. José Roberto Marques
UMC – CURSO BÁSICO DE ENGENHARIA
EXERCÍCIOS COMPLEMENTARES
1 – Dado o circuito elétrico abaixo, calcular:
a) A corrente gerada pela fonte.
b) A potência consumida pelo circuito.
c) A tensão nos resistores R4, R5, R7, R8 e R11.
d) A potência dissipada pelos resistores citados em (c ).
R6
I
fonte
R7
20 Ω
R4
50 Ω
R1
10 Ω
+
R8
16 Ω
R2
20 Ω
300V
R11
50 Ω
R9
18 Ω
R3
30 Ω
R5
10 Ω
R10
6Ω
R12
22 Ω
Solução:
Determine primeiramente os elementos que estão evidentemente em série.
R6
300V
R2
20 Ω
Req2 = R4 + R5 = 60
Req1 = R1 + R2 + R3 = 60
+
R7
20 Ω
R4
50 Ω
R1
10 Ω
R3
30 Ω
R5
10 Ω
R11
50 Ω
R9
18 Ω
Req4 = R11 + R12 = 72
fonte
Req3 = R7 + R8 = 36
I
R8
16 Ω
R10
6Ω
R12
22 Ω
R6 5 Ω
I
fonte
Req3 = 36 Ω
+
Req1 = 60 Ω
Req2 = 60 Ω
36 * 18
Req5 = _______ = 12
36 + 18
Depois disso, resolva os elementos resultantes que ficaram em paralelo.
R9
18 Ω
Req4 = 72 Ω
300V
R10
6Ω
Se dessa redução, resultar elementos em série, resolva-os.
1
Universidade de Mogi das Cruzes – Engenharia – Curso Básico
Prof. José Roberto Marques
R6 5 Ω
I
fonte
Req5 = 12Ω
Req4 = 72 Ω
Req6 = 12 + 6 = 18
Req2 = 60Ω
Req1 = 60Ω
+
300V
R10
6Ω
Verifique se ficaram elementos em paralelo e resolva-os.
R6 5 Ω
Req1 = 60
+
Ω
R4
Req2 = 60
300V
= 14,4
I
fonte
Ω
Req6= 18
Req4 = 72
18 * 72
_______
Req7 = 18 + 72
I
Ω
Verifique desse novo circuito se resultaram novos elementos em paralelo, resolva-os.
R6 5 Ω
q8
Re
I
fonte
=5
+1
=
4,4
300V
Req1 = 60 Ω
Req2 = 60 Ω
,4
19
+
Req7 = 14,4
Ω
2
Universidade de Mogi das Cruzes – Engenharia – Curso Básico
Prof. José Roberto Marques
Verifique agora se resultaram novos elementos em paralelo e resolva-os
I
fonte
Req1 = 60
Ω
Req2 = 60
Ω
60 * 60
_______
Req9 = 60 + 60 = 30
+
300V
Req7 = 19,4 Ω
I
Req8 =30 Ω
Req7 = 19,4 Ω
30 * 19,4
________
30 + 19,4
+
= 11,78
fonte
Req10 =
300V
I
fonte
+
Req10 = 11,78
300V
Ω
Quando o circuito resultar em um único resistor e a fonte podemos calcular a corrente que a fonte
fornece ao circuito:
a)
I fonte =
E
Req10
=
300
= 25,46 A
11,78
b) A potência fornecida pela fonte e consumida pelo circuito é:
Pcircuito = Pfonte = E * I fonte = 300 * 25,46 = 7638W
c) Tensão no resistor R4
Note que a tensão no ramos onde R4 está situado pode ser calculada diretamente a partir da tensão
da fonte utilizando o Req2:
3
Universidade de Mogi das Cruzes – Engenharia – Curso Básico
Prof. José Roberto Marques
R6 5 Ω
I
I
fonte
+
Req1 = 60
Ω
R4
Req2 = 60
Ω
300V
I R 4 = I R 5 = I Re q 2 ==
E
300
=
= 5 A porque R4 e R5 estão em série.
Req 2
60
A tensão em R4 será: V R 4 = R 4 * I R 4 = 50 * 5 = 250V porque R4 e R
E a potência dissipada pelo mesmo é:
PR 4 = I R 4 * V R 4 = 250 * 5 = 1250W
A tensão em R5 é: V R 5 = R5 * I R 5 = R5 * I R 4 = 10 * 5 = 50V
PR 5 = VR 5 * I R 5 = 50 * 5 = 250W
Tensão em R7:
O resistor R7 está o ramo do resistor equivalente Req8 no qual passa a corrente:
I Re q 8 =
300 300
=
= 15,46 A
Req8 19,4
Como R7 pertence ao conjunto de Req6 dentro de Req8, no qual a tensão é:
VRe q 7 = Req 7 * I Re q 8 = 14,4 *15,46 = 222,62V
Essa tensão é aplicada tanto no Req6 como no Req4 porque estão em paralelo, como R7 está no
ramo do Req6, vamos calcular essa corrente.
I Re q 6 =
VRe q 7
Req 6
=
222,62
= 12,38 A
18
Como R7 pertence, dentro de Req6 ao resistor Req5 vamos precisar da tensão em Req5, assim:
VRe q 5 = I Re q 6 * Re q5 = 12,38 *12 = 148,56V
A corrente no resistor Req3 que é onde se encontra R7 pode ser calculada de:
I Re q 3 =
VRe q 5
Req 3
=
VRe q 5
R7 + R8
=
148,56
4,127 A
36
A tensão no resistor R7 é:
V R 7 = I Re q 3 * R7 = 4,127 * 20 = 82,53V
PR 7 = VR 7 * I Re q 3 = 4,127 * 82,53 = 340,60W
Como R8 está em série com R7, a corrente nele é a mesma, ou:
VR8 = I Re q 3 * R8 = 4,127 * 16 = 66,02V
PR8 = VR 8 * I Re q 3 = 4,127 * 66,02 = 272,46W
4
Universidade de Mogi das Cruzes – Engenharia – Curso Básico
Prof. José Roberto Marques
Tensão no Resistor R11.
Note que R11 está inserido em Req4 que em paralelo com Req6 forma o Req7, assim a tensão no
ramo onde está R11 pode ser calculada de:
I Re q 4 =
V Req 7
Req 4
=
222,62
= 3,091A
72
V R11 = R2 * I Re q 4 = 50 * 3,091 = 154,55V
PR11 = I Re q 4 * VR11 = 3,091 *154,55 = 477,71W
2- O circuito abaixo tem duas cargas controladas pelas chaves S1 (R1) e S2(R2). Calcular a energia
gasta pelo circuito em kWh.
I2
I1
t0 = 0
+
t2=5A
S1
t1 = 10h
S2
t3 = 15h
220V
4Ω
R1
R2
6Ω
A potência dissipada por R1 é:
PR1 =
220 2
= 12100W = 12,1kW
4
A potência dissipada por R2 é:
PR 2 =
220 2
= 8066,67W = 8,0667 kW
6
P1 + P2 = 20,1667kW
P1= 12,1kW
P2 = 8,0667kW
5h
5h
5h
t
t1 = 0
t3 = 5h
t2 = 10h
t4 = 15h
A energia total é:
ε = 12,1 * 5 + 20,1667 * 5 + 8,0667 * 5 = 201,667 kWh
5