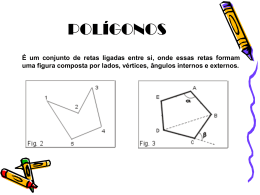
w POLÍGONOS
01. O polígono cuja soma do
gênero (no. de lados) com o número
de diagonais vale 45 é o:
a) Octógono
b) Eneágono
c) Decágono
d) Undecágono
e) Dodecágono
2) Prolongando-se os lados
AB e CD de um polígono convexo
regular ABCD..., obtém-se um ângulo
de 132º conforme ilustra a figura. De
acordo com o número de lados, esse
polígono é um:
1
2) (continuação)
a) Octógono
D á
b) Decágono
c) Undecágono
d) Pentadecágono
e) Icoságono
3) O ângulo interno do polígono
regular em que o número de diagonais
excede de 3 o número de lados é:
a) 60º
b) 72º
c) 108º
d) 150º
E) 120º
4) (continuação)
4) A moldura de um retrato é
formada por trapézios congruentes,
como está representado na figura
abaixo A moldura dá uma volta
abaixo.
completa em torno do retrato. Quantos
trapézios formam essa moldura?
2
4) (continuação)
a) 7
b) 8
c) 9
d) 10
e) 11
6) O polígono regular convexo
cujo ângulo interno é 7/2 do seu ângulo
externo é o:
a)
) Icoságono
g
b) Dodecágono
c) Decágono
d) Eneágono
e) Octógono
5) O ângulo interno de um
polígono regular de 170 diagonais
é igual a:
a) 80º
b) 170º
c) 162º
d) 135º
e) 81º
7) Em um polígono regular de n lados, de
vértices P1,P2,...,Pn, inscrito em uma
circunferência, observa-se que o vértice
P15 é diametralmente oposto ao vértice
P46 O valor
l
d n é:
é
P46.
de
A) 60
B) 62
C) 64
D) 66
E) 68
3
8) Num polígono convexo, o número
de lados é o dobro do número de
diagonais. Calcule o número de
lados do polígono.
w
w
w
w
w
a) 5
b) 6
c) 7
d) 8
e) 9
9) ABCDEF... é um polígono
convexo regular. Determine o número
d lados
l d
d
lí
b d que
de
desse
polígono,
sabendo
o ângulo BDE mede 144º.
4
a)
b)
c)
d)
e)
10) (FISCAL DO TRABALHO – ESAF)
Um polígono regular possui a partir de
cada um de seus vértices tantas
g
q
quantas são as diagonais
g
diagonais
de um hexágono. Cada ângulo interno
deste polígono mede em graus:
10
11
12
15
20
10) (continuação)
a) 140
b) 150
c) 155
d) 160
e) 170
11) A soma das medidas dos ângulos
internos de um polígono regular é
2160º Então o número de diagonais
2160º.
desse polígono, que não passam pelo
centro da circunferência que o
circunscreve, é:
5
11) (continuação)
a) 50
b) 60
c) 70
d) 80
e) 90
12) (continuação)
a) 6
b) 7
c) 13
d) 16
e) 17
12) Dois ângulos internos de um
polígono convexo medem 130o cada
um e os demais ângulos internos
d
128o cada
d um. O número
ú
d
medem
de
lados do polígono é:
13) Considere as afirmações sobre
polígonos convexos:
I) Existe apenas um polígono cujo
número de diagonais coincide
com o número de lados
II) Não existe polígono cujo número
de diagonais seja o quádruplo do
número de lados
6
13) (continuação)
III) Se a razão entre o número de
diagonais e o de lados de um polígono
é um número natural, então o número
de lados do polígono é ímpar
13) (continuação)
a) Todas as afirmações são verdadeiras
I e III são verdadeiras
b)
) Apenas
p
c) Apenas I é verdadeira
d) Apenas III é verdadeira
e) Apenas II e III são verdadeiras
14) A média aritmética dos ângulos
internos de um eneágono convexo vale:
15) Em qual dos polígonos convexos
a soma dos ângulos internos mais a
soma dos ângulos externos é de
1080º ?
) 40º
a)
b) 70º
c) 120º
d) 135º
e) 140º
a) Pentágono
b) Hexágono
c) Heptágono
d) Octógono
e) Eneágono
7
16) Um polígono regular tem vinte
diagonais. A medida em graus, de um
internos é:
de seus ângulos
g
a) 201º
b) 167º
c) 162º
d) 150º
e) 135º
17) (Continuação)
a)
) x < 120º
b) 120º < x < 130º
c) 130º < x < 140º
d) 140º < x < 150º
e) x > 150º
17) Um polígono regular convexo tem
o seu número de diagonais expresso
8 onde n é o seu
por n2 – 10n + 8,
número de lados. O seu ângulo
interno x é tal que:
18) O número de polígonos regulares
cuja soma dos ângulos externos não é
inferior à soma dos ângulos internos é:
a) 5
b) 4
c) 3
d) 2
e) 1
8
19) De dois polígonos convexos, um
tem a mais que o outro 6 lados e 39
diagonais. Então a soma total do
número de vértices e de diagonais
dos dois polígonos é igual a:
a) 63
b) 65
c) 66
d) 70
e) 77
20) (continuação)
de Augusto é o dobro da de Vinicius e o
quádruplo da de Romeu. Augusto
desloca-se em sentido oposto ao de
Vinicius e ao de Romeu. Após um certo
tempo, Augusto e Vinicius encontram-se
num determinado vértice.
20) (FISCAL DO TRABALHO – ESAF)
Augusto, Vinicius e Romeu estão no
mesmo vértice de um polígono regular.
N
d momento,
t os ttrês
ê começam
Num d
dado
a caminhar na borda do polígono. Todos
os três caminham em velocidades
constantes sendo que a velocidade
20) (continuação)
Logo a seguir, exatamente dois vértices
depois, encontram-se Augusto e Romeu.
O número de arestas do polígono é:
a) 10
b) 15
c) 12
d) 14
e) 11
9
w TEOREMA
w DE
21) Ache o perímetro do quadrilátero
ABCD, sendo que o triângulo ABC é
retângulo e o triângulo ACD é eqüilátero.
w PITÁGORAS
a)
b)
c)
d)
e)
17
18
19
20
21
dm
dm
dm
dm
dm
22) Qual o valor de w na figura?
10
a)
b)
c)
d)
e)
a)
b)
c)
d)
e)
11,8
12,2
13,4
14,6
15,8
4m
6m
8m
9m
10m
23) Dois círculos de raios 2m e 8m
são tangentes exteriormente e
tangentes a uma reta nos pontos A
e B. Qual o comprimento de AB?
24) Duas circunferências são
concêntricas (mesmo centro), e
seus raios medem 1,5 cm e 1,2 cm.
Encontre o comprimento da corda
da circunferência maior, tangente
à menor.
11
a)
b)
c)
d)
e)
a)
b)
c)
d)
e)
1,6
1,8
2,0
2,2
2,4
12
13
14
15
16
cm
cm
cm
cm
cm
25) Uma bola estava flutuando em
um lago, quando este congelou. A bola
foi então removida (sem quebrar o
gelo) deixando um buraco de 24 cm
gelo),
de diâmetro e 8 cm de profundidade.
Qual o raio da bola (em
centímetros)?
cm
cm
cm
cm
cm
12