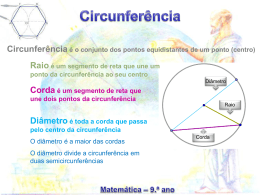
B3
CIRCUNFERÊNCIA E POLÍGONOS.
ROTAÇÕES
Circunferência
Circunferência é um conjunto de pontos do plano situados à mesma
distância de um ponto fixo (centro).
Corda é um segmento de recta cujos extremos são dois pontos quaisquer
da circunferência. Por exemplo, [ED], [AD] e [AB].
Diâmetro é uma corda que contém o centro da circunferência. Por exemplo
[ED].
Raio é um segmento de recta cujos os extremos são o centro e um ponto
qualquer da circunferência. Por exemplo, [CE], [CD] e [CA].
Arco é um segmento de circunferência compreendida entre dois ppontos
que lhe pertencem. Existem arcos menores, pois são menores que metade
da circunferência, e arcos maiores, porque são maiores que metade da
circunferência.
arco menor AB = arco AB
arco maior AB = arco ADB = arco AEB
A amplitude do arco AB representa –se AB
Equipa de formadores da Escola Profissional de Capelas
1
Ângulo ao centro
Ângulo ao centro é um angulo cujo vértice é o cento da circunferência
Por exemplo, ∠AOB e ∠COD
A cada ângulo ao centro corresponde uma corda e um arco: os que ficam
compreendidos entre os seus arcos.
Por exemplo, [AB] é a corda correspondente ao ∠AOB e o arco CD é o
arco correspondente ao ∠COD.
Propriedade
A amplitude de um ângulo ao centro é igual à amplitude do arco
correspondente. Simbolicamente, AÔB = AB e CÔD = CD.
Exemplos:
Considera a circunferência de centro O e determina as amplitudes de
∠AOB e ∠COD.
Resolução:
Como são ângulos ao centro, a sua amplitude é igual à
do arco correspondente. Logo, AÔB = AB = 55º e
CÔD = CD = 60º.
Equipa de formadores da Escola Profissional de Capelas
2
Ângulo inscrito
Ângulo inscrito é um ângulo cujo o centro é um ponto da circunferência e
cujos os lados contém cordas. Por exemplo, ∠ABC e ∠DEF.
Os lados do ângulo inscrito ABC intersectam a
circunferência em dois pontos, A e C. Diz-se que o
arco AC é o seu arco correspondente: arco
compreendido entre os seus lados. Ao arco ABC
chama-se arco capaz desse ângulo: arco que contém
o vértice.
Propriedade
A amplitude de um ângulo inscrito é metade da amplitude do arco
correspondente. Simbolicamente, ABC =
AC
DF
e DÊF =
2
2
Exemplos:
1. Considera a circunferência e determina A^BC e DÊF.
Resolução:
∠ABC e ∠DEF são ângulos inscritos.
AB
50º
=
= 25º
2
2
DF
60º
DÊF =
=
= 30º
2
2
ABC =
Equipa de formadores da Escola Profissional de Capelas
3
2. Determina ABC.
Resolução:
30º
= 15º, porque é um ângulo
2
DAE =
inscrito.
70º
= 35º, porque é um ângulo
2
AÊC =
inscrito.
AÊB = 180º - AÊC, isto é, AÊB = 180º - 35º, AÊB = 145º.
Como a soma das amplitudes dos ângulos internos de um triângulo é 180º,
145º + 15º + ABC = 180º, ou seja, ABC = 20º.
Propriedades dos ângulos, arcos e circunferências.
Numa circunferência ou em circunferências iguais:
• A ângulos ao centro iguais correspondem arcos iguais e reciprocamente.
• A ângulos ao centro iguais correspondem cordas iguais e
reciprocamente.
• A arcos iguais correspondem cordas iguais e reciprocamente.
Simbolicamente: COD = AOB ⇔ CD = AB ⇔ CD
= AB
Nota: Deve entender-se iguais como
geometricamente iguais.
Numa circunferência, ângulos inscritos no mesmo arco
têm a mesma amplitude.
ACD = ADB = AÊB = AFB =
AB
2
Equipa de formadores da Escola Profissional de Capelas
4
Um ângulo inscrito numa semicircunferência é um
ângulo recto porque a amplitude do arco
compreendido entre os seus lados é 180º, logo a
amplitude do ângulo correspondente é
180º
= 90º.
2
Uma recta tangente a uma circunferência é
perpendicular ao raio no ponto de tangência, ou
seja, CTA = 90º.
Uma recta perpendicular ao meio de uma corda
passa no centro da circunferência e divide ao meio
os arcos e os ângulos ao centro correspondentes.
ACD = DCB e AD = DB
Numa
circunferência,
arcos
e
cordas
compreendidas entre cordas paralelas são
geometricamente iguais.
AC = BD e AC = BD
Em consequência desta propriedade, qualquer
trapézio inscrito numa circunferência é isósceles.
Equipa de formadores da Escola Profissional de Capelas
5
Qualquer recta que contém o centro da
circunferência é um eixo de simetria, isto é, ao
dobrar a figura por essa recta, as duas partes
coincidem ponto por ponto.
Exemplos:
Considera a circunferência de centro O da figura. Sabendo que AT é
tangente à circunferência no ponto T e que BT = 70º, determinar OAT.
Resolução:
É necessário considerar o ∆[OAT] e determinar as amplitudes dos seus
ângulos internos.
AOT = BT = 70º porque é um ângulo ao centro.
OAT = 90º porque a tangente é perpendicular ao raio no ponto de
tangência.
Então, OAT = 180º - 70º - 90º = 20º porque a soma das amplitudes dos
ângulos internos de um triângulo é 180º.
Polígonos
Polígono é uma figura geométrica limitada apenas por segmentos de recta.
Existem polígonos côncavos e convexos.
Equipa de formadores da Escola Profissional de Capelas
6
Num polígono podem considerar-se ângulos internos e ângulos externos.
Propriedades
A soma das amplitudes dos ângulos externos de um polígono convexo é
de 360º.
A amplitude de um ângulo externo de um polígono convexo regular
com n lados é
360º
.
n
A amplitude de um `^angulo interno de um polígono convexo regular
com n lados é 180º -
360º
.
n
A soma das amplitudes dos ângulos internos de um polígono convexo
com n lados é 180ºn – 360º.
Um polígono diz-se inscrito numa
circunferência se todos os seus vértices são
pontos da circunferência que se diz
circunscrita ao polígono.
Um polígono regular pode sempre inscrever-se numa circunferência.
O lado de um hexágono regular inscrito numa
circunferência é igual ao raio.
Equipa de formadores da Escola Profissional de Capelas
7
Exemplos:
1. Determinar a amplitude de um ângulo interno de um eneágono regular.
Resolução:
Como um eneágono tem 9 lados, a amplitude do seu ângulo interno é:
180º -
360º
= 180º - 40º = 140º.
9
2. Determinar o perímetro de um hexágono regular inscrito numa
circunferência com 25,12 cm de perímetro.
Resolução:
Para determinar o perímetro é necessário conhecer a medida do lado que é
igual ao raio da circunferência. Ora, PΟ= 2πr
2πr = 25,12 ⇔ r =
25,12
⇔r=4
2π
O lado do hexágono mede 4 cm. Então o seu perímetro é 6 x 4 = 24 cm.
A soma das amplitudes dos ângulos opostos de um
quadrilátero inscrito numa circunferência é 180º.
â + b = 180º e c + d = 180º
A área de um sector circular de raio r, cujo arco tem
amplitude α, é:
A=
απr 2
360
A área de um polígono regular é:
A=
Perimetroxapótema
2
Equipa de formadores da Escola Profissional de Capelas
8
3. Determina a área de um pentágono regular com 6 cm de lado inscrito
numa circunferência de raio 6,5 cm.
Resolução:
Aplicando o Teorema de Pitágoras, ao triângulo rectângulo assinalado,
determina-se a apótema do pentágono,
ap2 + 32 = 6,52
⇔ ap2 + 9 = 42,25 ⇔ ap2 = 42,25 - 9 ⇔
⇔ ap2 = 33,25 ⇔ ap = 33,25 ⇔
⇔ ap = 5,8
A=
P × ap
6 × 5 × 5,8
=
= 87 cm2
2
2
Rotações e isometrias
Ângulo orientado é um ângulo onde está definido um sentido que pode ser
positivo ou negativo.
Sentido negativo – sentido do movimento dos ponteiros do relógio.
Sentido positivo – sentido contrário ao movimento dos ponteiros do
relógio.
Equipa de formadores da Escola Profissional de Capelas
9
Rotação do centro O e amplitude α é uma transformação geométrica que
a cada ponto A associa um ponto A’ tal que AOA’ = α e AO = AO’.
A rotação de centro O e amplitude 80º, R(O, 80º) transforma o ∆[OAB] no
∆[OA'B’]. O ∆[OA'B’] diz-se imagem do ∆[OAB].
Propriedades
Numa rotação:
Um segmento de recta é transformado num segmento de recta
geometricamente igual.
Um ângulo é transformado noutro com o mesmo sentido e
geometricamente igual.
Exemplos:
Construir a imagem do polígono pela rotação de centro O e amplitude –80º,
usando o transferidor e o compasso.
Resolução:
Equipa de formadores da Escola Profissional de Capelas
10
Isometria é a transformação geométrica que transforma uma figura em
outra geometricamente igual.
As rotações, as translações e as simetrias são isometrias.
Equipa de formadores da Escola Profissional de Capelas
11
APLICA O QUE APRENDESTE
1. Na circunferência de centro O da figura, [AC] é o lado de um hexágono
regular nela inscritível.
1.1.
1.2.
1.3.
Determina AOC, ABC e ACB.
Sendo AC = 2 cm, calcula o
comprimento do arco AC.
Classifica o ∆[ABC] quanto aos ângulos.
2. Considera o trapézio [ABCD] inscrito na circunferência. Sabendo que
[AB] é o lado de um pentágono regular
inscritível na circunferência e que DC = 2AB,
determina a amplitude dos ângulos internos do
trapézio.
3. Na circunferência da figura, DCA = 50º e CAB = 55º. Determina :
3.1. CFB
3.2. DÊA
Equipa de formadores da Escola Profissional de Capelas
12
4. Considera a circunferência de centro O da figura. Sabendo que AC =
80º e DE = 30º, determina.
4.1.
4.2.
4.3.
4.4.
4.5.
4.6.
DAE
DCE
ADC
AFD
DFE
ABC
5. Na figura, BC é tangente à circunferência
de centro O no ponto D, AF = 100º e ED =
1
DF. Determina as amplitudes dos
2
ângulos internos do ∆[ABC].
6. Considera a circunferência de centro O da figura. Sabendo que AB =
140º e que AC e BC são tangentes à circunferência em A e B,
respectivamente.
6.1. Calcula OÂB e ABC.
6.2. Classifica o ∆[ABC] quanto aos
lados.
6.3. O gráfico traduz uma situação de
proporcionalidade. Indica o tipo e a
constante de proporcionalidade.
Equipa de formadores da Escola Profissional de Capelas
13
7. Na circunferência de centro O da figura, AD é tangente no ponto A e
BÂD = 80º. Determina:
7.1. AOB
7.2. ACB
8. Considera a circunferência de centro O da figura. Sabendo que CD =
100º e que AB é tangente no ponto B, determina:
8.1. DBC
8.2. BCD
8.3. ABC
8.4. ABD
8.5. BÂC
8.6. BDO
9. Averigua se existe um polígono regular cuja amplitude do ângulo
interno é 162º. Em caso de existir, indica o número de lados.
10. Quais das afirmações seguintes são verdadeiras?
I)
Num triângulo, a amplitude do ângulo externo é igual à soma das
amplitudes dos ângulos internos não adjacentes.
II) Num triângulo, a soma das amplitudes dos ângulos internos é 180º.
III) Num quadrilátero inscrito numa circunferência, os ângulos opostos
são suplementares.
IV) Num triângulo rectângulo, a hipotenusa é igual à soma dos catetos.
A) Todas B) I, II e III
C) II, III e IV
D) I, II e IV
Equipa de formadores da Escola Profissional de Capelas
14
11. Considera um hexágono regular com 4 cm de lado inscrito numa
circunferência de centro O. Determina:
11.1. A área da parte colorida da figura;
11.2. A amplitude do ângulo interno e a amplitude
do ângulo externo do hexágono.
12. Num estudo estatístico sobre os níveis de Matemática dos alunos de
uma turma, elaborou-se um gráfico circular com 2 cm de raio.
Determina a área do sector circular correspondente ao nível 4.
13. Constrói a imagem do ∆[ABC] pela rotação de centro O e amplitude
45º.
Equipa de formadores da Escola Profissional de Capelas
15