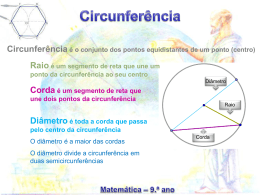
Catarina Ribeiro
1
 Vamos Recordar:
Circunferência de centro C e raio r é o lugar geométrico de
todos os pontos do plano que estão à mesma distância r de um
ponto fixo C.
Círculo de centro C e raio r é o lugar geométrico de todos os pontos do
plano que estão a uma distância menor ou igual a r de um ponto fixo C.
Raio é o segmento de recta que une um ponto da circunferência com
o seu centro.
Corda é qualquer segmento de recta cujas extremidades são dois
pontos da circunferência.
Diâmetro é acorda que passa pelo centro da circunferência, sendo por isso a
maior corda.O diâmetro divide a circunferência em duas semicircunferências.
2
Arco de circunferência é qualquer porção de circunferência
compreendida entre dois pontos que se dizem extremidades
do arco.
Arco menor é qualquer arco menor que uma semicircunferência e que se pode
designar com duas letras. De acordo com a fig. seria o arco AF.
Arco maior é qualquer arco maior que uma semicircunferência e que se pode
designar com três letras. De acordo com a fig. seria o arco FEA.
3
 Posição relativa de uma recta e uma circunferência
A recta r intersecta a circunferência de centro C,
em dois pontos. r é secante à circunferência.
A recta t intersecta a circunferência no ponto T.
t é tangente à circunferência.
A recta s não intersecta a circunferência de centro C.
s é exterior à circunferência.
4
 Posição relativa de duas circunferências
As circunferências
são exteriores
As circunferências
são tangentes exteriores
As circunferências
são secantes
5
 Simetrias numa circunferência
O eixo de simetria de uma figura divide-a em duas partes geometricamente iguais.
Toda a recta que passa pelo centro da circunferência é eixo de simetria da
circunferência. A circunferência tem uma infinidade de eixos de simetria.
A tangente a uma
circunferência é
perpendicular
ao raio que passa pelo
ponto de tangência, T.
Numa circunferência a recta
perpendicular ao meio de
uma corda passa pelo centro
da circunferência.
Numa circunferencia:
arcos (ou cordas)
compreendidos entre
cordas paralelas são
geometricamente i guais
6
 Ângulo ao centro
Ângulo ao centro é um ângulo que tem o vértice no centro da
circunferência e cada lado contém um raio dessa circunferência.
 AOB
é um ângulo ao centro
7
 Amplitude do ângulo ao centro
A cada ângulo ao centro corresponde um
arco, que é a sua intersecção com a
circunferência.
Reciprocamente,
a
cada
arco
corresponde um ângulo ao centro
A amplitude
do ângulo ao centro é
igual
à
amplitude
correspondente.
do
arco
8
Exercício:
Determine a amplitude do ângulo x e do seu arco correspondente.
1.
2.
A amplitude do arco correspondente ao ângulo é 120º.
xˆ  60 º
A amplitude do arco correspondente é também 60º.
9
 Ângulo inscrito
Ângulo inscrito é um ângulo que tem o vértice na circunferência e
os lados contém cordas dessa circunferência.
 AVB
é um ângulo inscrito
10
Na figura, [ABC] é um triângulo equilátero.
C
A Cˆ B  60 º
Logo,
60°
O arco AB tem de amplitude 120º, porque
A Oˆ B  120 º
Portanto,
O
1
ˆ
AC B  AÔB
2
A
120°
B
A amplitude do ângulo inscrito é igual a metade da amplitude
do ângulo ao centro correspondente.
OU
A amplitude do ângulo inscrito é igual a metade da amplitude
do arco que ele contém.
11
Alguns Exemplos:
12
1.
Exercícios: determine a amplitude dos ângulos pedidos.
yˆ  86 º
86º
xˆ 
2
 43 º
2.
40º
xˆ 
 20 º
2
yˆ  40 º
13
Propriedades
1. Ângulos inscritos que contêm o mesmo arco
A Cˆ B  A Dˆ B  A Eˆ B ,
50º
porque os três ângulos contêm o mesmo
arco AB.
50º
Então,
Os ângulos inscritos que
contêm o mesmo arco são
50º
geometricamente iguais.
14
2. Ângulos inscritos numa semi-circunferência
90º
A Cˆ B  A Dˆ B  A Eˆ B  90 º
90º
90º
Então,
Um ângulo inscrito
numa semi-circunferência
é um ângulo recto.
15
4. Ângulos opostos de um quadrilátero inscrito numa circunferência
aˆ  2 A Bˆ C
bˆ  2 A Dˆ C
aˆ  bˆ  2 ( A Bˆ C  A Dˆ C )
Mas,
aˆ  bˆ  360 º
Portanto,
2 ( A Bˆ C  A Dˆ C )  360 º
Logo,
A Bˆ C  A Dˆ C  180 º
Então, A soma dos ângulos opostos de um quadrilátero inscrito numa
circunferência é 180º.
16
3. Ângulo ao centro, arcos e cordas
Na figura estão representados
dois ângulos ao centro iguais, as cordas e
os arcos correspondentes.
C D  A B  40 º
CD  AB
Então,
Numa
circunferência,
as
cordas correspondentes a dois ângulos
ao centro iguais são geometricamente
iguais, e reciprocamente.
Numa circunferência, os arcos correspondentes a dois ângulos ao
centro iguais são geometricamente iguais, e reciprocamente.
17
4. Ângulo ao centro, arcos e cordas
Um arco de amplitude 50º corresponde a um
ângulo ao centro de amplitude de 50º.
Embora os três arcos tenham 50º de amplitude, os seus comprimentos são diferentes.
O comprimento de cada um depende do raio da circunferência que o contém.
Quanto maior for o raio da circunferência, maior é o comprimento do arco.
Se o raio da circunferência que contém o arco EF, de amplitude 50º, for 2 cm
o seu comprimento é:
18
1.
Exercícios: determine a amplitude dos ângulos pedidos.
Pela propriedade 1 vêm:
xˆ  62 º
yˆ  2  62 º  124 º
2.
A amplitude do arco correspondente ao ângulo
(inscrito) de 130º é de 260º.
Logo,
xˆ  360 º  260 º
 100 º
19
3.
Usando a propriedade 2 vêm:
x̂  180 º  ( 90 º  30 º ) 
 180 º  120 º 
 60 º
4.
O Aˆ B  A Bˆ O
Então,
B Oˆ A  180 º  84 º  96 º
Logo,
96 º
xˆ 
 48 º
2
20