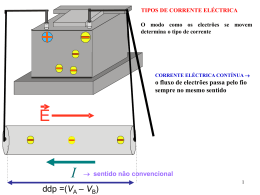
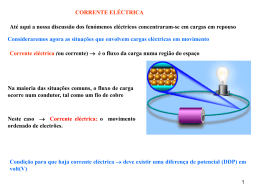
Introdução ao Estudo da Corrente Eléctrica
•
Num metal os electrões de condução estão “dissociados” dos seus átomos de
origem passando a ser partilhados por todos os iões positivos do sólido, e
constituem desta forma um mar de electrões “livres”:
Os electrões movimentam-se, mas a sua velocidade média é nula:
não há corrente eléctrica.
•
Os transportadores de carga estão sempre em movimento, devido à agitação
térmica.
•
Cargas eléctricas em movimento orientado originam a corrente eléctrica.
1/23
•
Para haver corrente eléctrica é necessário que a velocidade média ou
velocidade de deriva dos electrões de condução seja diferente de zero.
•
Quando há uma corrente eléctrica, os electrões têm velocidades diferentes,
mas considera-se uma velocidade média:
•
Apesar de serem os electrões os responsáveis pela corrente eléctrica num
condutor, convencionou-se que o sentido da corrente é o das cargas positivas.
•
Esta convenção foi estabelecida antes de se conhecerem os mecanismos de
condução eléctrica nos metais (antes da descoberta do electrão por JJ Thomson, 1897).
2/23
Intensidade de Corrente Eléctrica
•
Para haver corrente eléctrica é necessário que actue uma força nas cargas, i.é
terá de existir um campo eléctrico.
•
A diferença de potencial, V, que permite a existência de uma corrente eléctrica
entre dois pontos afastado de L do condutor é:
V
E=
L
•
A intensidade de corrente eléctrica define-se como a quantidade de carga
eléctrica que atravessa uma secção recta de um condutor por unidade de tempo:
I=
•
•
∆Q
∆t
ou, no caso de a corrente não ser estacionária, isto é, de ser variável no tempo:
dQ
I=
dt
A unidade SI de corrente eléctrica é o Coulomb por segundo, ou Ampére [A].
3/23
Intensidade de Corrente Eléctrica
•
Nem sempre são os electrões os responsáveis pela corrente eléctrica:
– Num acelerador de partículas a corrente é provocada pelo movimento de
todas as partículas carregadas presentes (electrões, positrões, protões,
etc...).
– No caso de um electrólito a corrente é transportada pelos iões positivos e
negativos, que se movem em sentidos opostos.
I=
•
•
•
•
∆Q
= n ⋅ q ⋅ A ⋅v d
∆t
n número de transportadores de carga por unidade de volume,
q carga eléctrica dos transportadores
A secção recta do volume onde se dá o transporte da corrente
vd velocidade de transporte ou de deriva.
4/23
Resistência e resistividade eléctrica
•
A corrente eléctrica num condutor é provocada por um campo eléctrico no interior
do condutor (nestes casos, o condutor não está em equilíbrio electrostático):
– Os electrões de condução estão sujeitos a uma aceleração no interior do
condutor.
– No entanto a sua velocidade não aumenta indefinidamente, devido às
frequentes colisões com os iões da rede cristalina, originando o
aquecimento do material.
– Quando se atinge o regime estacionário, o trabalho da força eléctrica é
igual ao trabalho das forças de resistência: a energia cinética média dos
electrões é constante.
•
Define-se resistência eléctrica como a razão entre a diferença de potencial
entre os extremos de um condutor e a intensidade da corrente que o percorre:
R=
V
I
5/23
Resistência e resistividade eléctrica
R pode ser relacionada com o comprimento do condutor L , a secção do condutor
A e uma propriedade do material denominada resistividade ρ :
L
R=ρ
A
A unidade SI de resistência eléctrica é o Volt por Ampére, denominada Ohm [Ω].
6/23
Resistência e resistividade eléctrica
O inverso da resistividade eléctrica é a condutividade eléctrica σ ,
1 L
R= ⋅
σ A
Material
Prata
Resistivida
de a 20°C
Ω·m]
[Ω
1,6 × 10-8
Cobre
1,7 × 10-8
Alumínio
2,8 × 10-8
Ferro
10 × 10-8
Germânio
Resistividade eléctrica do cobre
em função da temperatura
0,45
Madeira
108 – 1014
Vidro
1010 – 1014
Borracha dura
1013 – 1016
7/23
Resistividade eléctrica vs. Temperatura
Resistividade aumenta com T em condutores
ρ (T ) = ρ o [1 + α (T − To )]
α - coeficiente de temperatura da resistividade
Metal
Resistividade
diminui com T
Semicondutor
ρ (T < TC ) = 0
Supercondutor
8/23
Lei de Ohm
Para metais verifica-se experimentalmente que
V =RI
, R constante
Lei de Ohm
óhmico
não-óhmico
9/23
Efeito de Joule
•
•
Durante a condução de corrente eléctrica observa-se, no interior do condutor,
uma contínua transformação de energia eléctrica em energia térmica. Este
fenómeno designa-se por efeito de Joule:
– Este aquecimento deve-se ao mecanismo de colisões dos electrões livres
com os iões positivos da rede cristalina durante a condução. Estas
constantes colisões explicam a existência de uma velocidade de deriva
constante.
– Os electrões estão constantemente a receber energia do campo eléctrico,
mas ela é rapidamente transferida para o condutor, sob forma de energia
térmica: durante cada colisão o electrão perde todo o excesso de energia
cinética adquirido.
– O aumento de temperatura leva à transferência de energia do condutor para
o exterior, sob a forma de calor.
Potência dissipada por efeito de Joule num condutor com resistência R ,
submetido a uma diferença de potencial V e atravessado por uma corrente I
Wr = V ∆Q
⇒
V2
P =V I = R I =
R
2
10/23
10/23
Força Electromotriz
•
•
•
•
Para manter uma corrente eléctrica constante num circuito devemos ter
uma fonte de fornecimento de energia eléctrica também constante. Um
dispositivo que fornece energia eléctrica é uma fonte de força
electromotriz (f.e.m.).
São exemplos de fontes de força electromotriz as baterias e os
geradores.
Uma bateria ideal é uma fonte de f.e.m. que
mantém uma diferença de potencial constante
entre os seus terminais, independentemente da
intensidade da corrente que a percorre:
Uma bateria real tem sempre uma certa
resistência interna: a tensão entre os seus
terminais é igual à sua força electromotriz menos
a queda de tensão na sua resistência interna:
11/23
11/23
Leis de Kirchhoff
•
•
Apesar de os circuitos eléctricos poderem ser muito complexos, a sua análise
pode ser efectuada por intermédio de leis muito simples, as leis de Kirchhoff.
A lei dos nodos (ou dos nós)
a soma das correntes que entram num ponto do
circuito é igual à soma das correntes que saem
desse ponto:
•
∑ Ientram = ∑ Isaem
•
Consequência da lei da conservação da carga.
12/23
12/23
Leis de Kirchhoff
•
Lei das malhas
é nula a soma de todas as variações de potencial ao longo de qualquer percurso
fechado:
Atenção à convenção de sinais!
Para a queda de tensão num gerador toma-se o sinal do pólo por onde se entra, ao
circular.
Para a queda de tensão numa resistência toma-se o sinal positivo quando se circula
no sentido arbitrado para a corrente (e vice-versa).
13/23
13/23
Leis de Associação de Resistências
•
Associação em série
A corrente é a mesma em todas as
resistências.
A diferença de potencial (d.d.p.) V é
igual à soma das d.d.p. em cada
resistência.
Req = R1 + R2 + ... + Rn
•
Associação em paralelo
A corrente total é a soma da corrente
que passa em cada resistência.
A d.d.p. em cada resistência é igual
em todas as resistências.
1
1
1
1
=
+
+ ... +
Req R1 R2
Rn
14/23
14/23
Carga de Condensadores
•
•
•
•
Um circuito com uma resistência e um condensador é um circuito RC.
Neste tipo de circuito a corrente não permanece constante, mas varia com o
tempo.
Um exemplo prático de um circuito deste tipo é o circuito de alimentação de um
flash.
Durante o processo de carga de um condensador a intensidade de corrente
diminui à medida que a carga no condensador aumenta: já não falamos de
correntes estacionárias, mas de correntes transitórias.
Num circuito deste tipo a carga, assim como a intensidade de corrente varia de
forma exponencial. Estando o condensador inicialmente descarregado:
−t τ 

Q (t ) = Qf  1− e


,
I (t ) = Io e
−t τ
15/23
15/23
Carga de Condensadores
A duração do processo de carga depende do produto entre os valores da resistência
R e da capacidade do condensador C, designando-se t = RC por constante de
tempo.
O que acontece à energia fornecida pelo gerador ao circuito?
16/23
16/23
Descarga de Condensadores
•
Supondo agora que o condensador se encontra inicialmente com uma carga
Qo e se liga a uma resistência, através da qual se descarrega, a análise da
situação é ainda mais simples, dada a ausência do gerador:
Q (t ) = Qo e
−t τ
,
I (t ) = −Io e
−t τ
O facto de a corrente ser negativa na equação anterior significa apenas que tem
sentido contrário ao escolhido na figura:
•
Para um condensador que se descarregue desta forma, a constante de tempo, t ,
corresponde ao tempo ao fim do qual a carga é Q = Qo/e, ou seja, cerca de 37%
da carga inicial.
17/23
17/23
Aparelhos de Medida: Galvanómetro
Dispositivos que permitem medir as grandezas eléctricas num circuito de corrente
contínua:
– Amperímetro ➜ medida da intensidade de corrente
– Voltímetro ➜ medida da diferença de potencial
– Ohmímetro ➜ medida da resistência eléctrica
Por vezes estes instrumentos estão incluídos num único aparelho: o multímetro.
O principal componente de um amperímetro e de um voltímetro é um
galvanómetro: aparelho cuja leitura é proporcional à corrente que o atravessa.
18/23
18/23
Aparelhos de Medida: Galvanómetro
•
As duas propriedades mais importantes num
galvanómetro são:
– A resistência interna do galvanómetro, Rg .
– A corrente necessária para provocar a
deflexão máxima (sobre toda a escala), Ig .
•
Valores típicos destas grandezas: Rg = 10-100Ω,
Ig = 0,5 mA.
19/23
19/23
Aparelhos de Medida: Amperímetros e Voltímetros
• Para medir uma diferença de potencial através de um
elemento de um circuito, o voltímetro deve ser ligado
em paralelo com esse elemento.
• Para medir uma corrente eléctrica através de um
elemento de um circuito, o amperímetro deve ser
ligado em série com esse elemento.
A resistência interna do voltímetro deve ser grande
(idealmente infinita) comparada com a do elemento
através do qual se pretende medir a diferença de
potencial.
A resistência interna do amperímetro deve ser
pequena (idealmente nula) comparada com a do
ramo do circuito onde se pretende medir a corrente
eléctrica.
20/23
20/23
Aparelhos de Medida: Amperímetro
• Para construir um amperímetro liga-se um galvanómetro em paralelo com uma
resistência pequena (shunt), relativamente à resistência interna do galvanómetro:
• A maior parte da corrente passa pela resistência em derivação (shunt), sendo a
resistência interna do amperímetro assim construído, muito menor do que a do
galvanómetro de partida:
 1
1
Ra = 
+

R
Rs 

g
−1
=
Rg ⋅Rs
Rg + Rs
≈ Rs
, Rs = Rg
21/23
21/23
Aparelhos de Medida: Voltímetro
• Para construir um voltímetro liga-se um galvanómetro em série com uma
resistência elevada, relativamente à resistência interna do galvanómetro:
• Deste modo a resistência interna do voltímetro assim construído é muito mais
elevada que a do galvanómetro de partida:
Rv = Rg + Rs ≈ Rs
22/23
22/23
Aparelhos de Medida: Ohmímetro
• Para construir um ohmímetro liga-se um galvanómetro em série com uma
resistência Rs e uma fonte de força electromotriz e .
• Os valores de Rs e de e são escolhidos de modo a obter a deflexão máxima do
ponteiro com os terminais a e b em curto-circuito:
– A deflexão máxima indica resistência nula entre os terminais a e b .
– Quando os terminais são ligados a uma resistência desconhecida R , a corrente
no galvanómetro é I = e / (R+Rs+Rg), inferior a Ig. A escala pode ser calibrada
para dar uma leitura directa de R (atenção que esta escala não é linear).
23/23
23/23