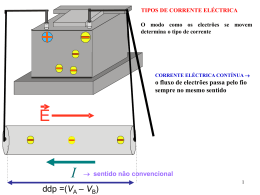
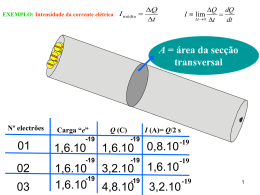
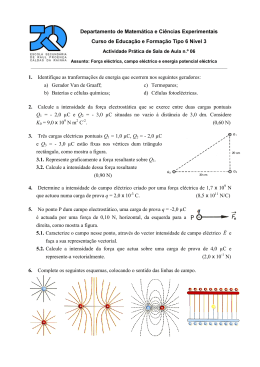
CORRENTE ELÉCTRICA
Até aqui a nossa discussão dos fenómenos eléctricos concentraram-se em cargas em repouso
Consideraremos agora as situações que envolvem cargas eléctricas em movimento
Corrente eléctrica (ou corrente)  é o fluxo da carga numa região do espaço
Na maioria das situações comuns, o fluxo de carga
ocorre num condutor, tal como um fio de cobre
Neste caso  Corrente eléctrica: o movimento
ordenado de electrões.
Condição para que haja corrente eléctrica  deve existir uma diferença de potencial (DDP) em
volt(V)
1
Aplicando-se uma diferença de potencial:
Criam-se pólos positivos e negativos nos extremos
2
Fonte
ddp =(VA – VB)
VB
VA
+
O pólo positivo é de maior potencial (VA)
O pólo negativo é de menor potencial (VB)
3
+
Não
há
corrente
eléctrica  as cargas
se movimentam em
todas as direcções
4
Corrente elétrica é o movimento ordenado
de cargas elétricas
+
Convencionalmente definimos a
corrente eléctrica como a direcção
do fluxo de carga positiva
Q é a quantidade de carga que
atravessa a área A no intervalo de
tempo t:
E
I média 
Q
t
Corrente eléctrica instantânea
Q dQ

t  0 t
dt
I  lim
I
 sentido não convencional
ddp =(VA – VB)
Unidade no SI: ampère (A):
1 A = 1 C/s
5
Podemos ter dois ou mais tipos de partículas que se deslocam, com cargas de ambos os sinais
Um feixe de protões positivamente carregados num acelerador de partículas, a corrente está na
direcção do movimento dos protões.
Nos gases e electrólitos, a corrente é o resultado do fluxo de partículas carregadas positiva e
negativamente
+
++
+
Líquido
+
+
Gás
Sólido
6
CONDUTORES IÓNICOS
iões +
++
+
Iões  Corrente elétrica iônica  é o movimento ordenado de iões
Portador de carga móvel
7
Modelo estrutural  relaciona a corrente macroscópica ao movimento das partículas
carregadas
Volume do cilindro :V= Axe
n
N
V

nº de portadores móveis de cargas
unidade de volume
 número de portadores no elemento de volume:
N=nV=nAxe
A carga móvel Q neste volume:
Q= número de portadores  carga por portador = Nq=(nAxe)q
Os portadores se deslocam ao longo do comprimento do condutor com uma velocidade média
constante chamada de velocidade de migração (ou de deriva - drift)  vd
Distância percorrida pelos portadores de carga num intervalo de tempo t 
Supomos xd = xe
I
Q
 nqv d A
t

xd = vdt
Q = Nq = (nAxe)q = (nAvdt)q
 relaciona uma corrente I macroscópica com
elementos microscópicos da corrente n, q, vd
8
Uma representação esquemática do movimento
ziguezague de um portador de carga num condutor
em
As mudanças de sentido são devidas a colisões com átomos
no condutor.
A resultante do movimento dos electrões está na direcção
oposta à direcção do campo eléctrico
A DENSIDADE DE CORRENTE J NO CONDUTOR
I
J   nqv d
A
Unidades do SI: ampères por metro quadrado:
A
m2
- Quando não existe ddp através do condutor, os electrões do condutor realizam movimento
aleatório similar àquele das moléculas de gás  visto anteriormente na teoria cinética
(Termodinâmica).
Esse movimento aleatório está relacionado à temperatura do condutor.
- Quando existe ddp o movimento dos electrões devido à força eléctrica é sobreposto ao seu
movimento aleatório para fornecer uma velocidade média cujo módulo é a velocidade de
migraçãp , vd
9
Quando os electrões colidem com o átomo do metal durante o seu movimento,
transferem energia para o átomo
 causando um aumento da energia vibracional dos átomos  aumento da
temperatura
Na verdade este é um processo que envolve três etapas :
• A energia no instante em que a ddp é aplicada  é a energia potencial eléctrica
associada ao campo eléctrico e aos electrões.
• Esta energia é transformada em energia cinética pelo trabalho realizado pelo
campo eléctrico sobre os electrões.
• Quando os electrões colidem com os átomos do metal uma parte da energia
cinética é transferida para os átomos esse soma à energia interna do sistema
10
Exemplo: Velocidade de Migração num Fio de Cobre
11