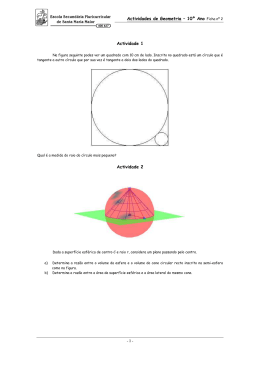
Unidade 10 – Geometria Espacial
Esfera
Esfera
Na série anterior, você
estudou dois dos
chamadas corpos
redondos: o cilindro e o
cone.
Estudaremos outro
sólido que sem dúvida,
aparece com extrema
frequência no cotidiano:
a esfera.
Esfera
Conceito: Considere um ponto P do espaço
e um segmento de medida R. Chama-se
esfera com centro no ponto P e raio de
medida R o conjunto dos pontos do espaço
cuja distância ao ponto P menor do que ou
igual a R.
Superfície esférica
Denomina-se superfície esférica de centro P
e raio de medida R o conjunto dos pontos do
espaço cuja distância ao ponto P é igual a R.
Secção de uma esfera
Se um plano α, intersecta uma esfera, determina
sobre ela uma secção plana. Essa secção é sempre
um círculo.
Se um diâmetro da esfera estiver contido no plano
α, a secção plana é denominada círculo máximo.
Secção de uma esfera
Para você fazer – p. 25
Na figura a seguir, o raio da esfera mede 10 cm , e a distância
do centro desta ao plano β é igual a 8 cm. Calcule a área da
secção plana determinada pela intersecção do plano b com a
esfera:
Assim, a área de secção, determinad a pela
intersecção do plano β e a esfera, é igual a
A = π . r 2 → A = π .6 2 = 36π cm 2
d
8
10
Por meio do Teorema de Pitágoras, temos :
10 2 = 82 + d 2 → d = 6cm
Você se lembra
Para você fazer – p. 26
Observe uma semiesfera de raio R, um cilindro
circular reto de raio da base e altura medindo R e
um cone circular reto cujo vértice coincide com a
base do cilindro. Considere ainda que esses sólidos
estejam apoiados sobre um mesmo plano α.
Para você fazer – p. 26
a) Imagine um plano b, paralelo ao plano a, que
intersecta a semiesfera e o cilindro
(consequentemente o cone). Que figuras planas o
plano b determina na semiesfera e no sólido
compreendido entre o cilindro e o cone?
Plano β
As figuras determinadas pelo plano b na semiesfera e no sólido compreendido
entre o cilindro e o cone são, respectivamente, um círculo e uma coroa circular.
Para você fazer – p. 26
b) Sendo h a distância entre os planos a e b,
calcule, em função de h e R, as áreas das
figuras planas descritas anteriormente.
⇒ Na semiesfera, temos que R 2 = h 2 + r 2 → r 2 = R 2 − h 2
Assim, a área do cículo determinad o pelo β é π R 2 − h 2
⇒ No sólido compreendido entre o cilindro e o cone, a área
(
da coroa é igual a π R 2 − h 2 .
(
)
Mas, r = h, pois o triângulo retângulo, cujos catetos medem r e h,
é semelhante ao triângulo retângulo isósceles, cujos catetos
medem R.
Assim, a área da coroa circular é igual a π R 2 − h 2 .
(
)
)
Para você fazer – p. 26
c) O que você observou em relação às áreas das duas
figuras plana? Com base nessa observação, o que
se pode concluir a respeito dos volumes da
semiesfera e do sólido compreendido entre o cilindro
e o cone?
Resposta: As áreas do círculo e da coroa circular são
iguais. Assim, como o plano β é genérico, qualquer
plano que intersectar a semiesfera e o sólido
compreendido entre o cilindro e o cone determinará
secções de mesma área. Pelo Princípio de Cavalieri,
os volumes dos dois sólidos são iguais.
Para você fazer – p. 26
d) Encontre uma expressão que permita medir
o volume da semiesfera.
Se os volumes dos dois sólidos são iguais, temos que :
Vsemiesfera = Vcilindro − Vcone
Vsemiesfera
1
= π .R .R − π .R 2 .R
3
Vsemiesfera
2
2 3
= .πR
3
Volume da esfera
O volume de um sólido é o espaço ocupado
por ele.
Por exemplo: quando dizemos que o volume
de um cilindro é igual a 1 metro cúbico
significa que o espaço ocupado por ele é
equivalente ao espaço ocupado por um cubo
cujas arestas medem 1 metro.
Mas, como medir o espaço ocupado por uma
esfera?
Volume da esfera
Com base do exercício anterior, concluímos
que, para medir o volume de uma
semiesfera, basta conhecer a medida de seu
raio.
Como o volume de uma esfera é duas vezes
o volume de uma semiesfera, temos que:
Vesfera
2 3
4 3
= 2. .πR ou Vesfera = .πR
3
3
Para você fazer – p. 27
1) A medida aproximada do raio da bola de
futebol na figura a seguir é 11 cm. Calcule o
volume aproximado contido no interior dessa
bola.(Utilize π = 3,14).
Sendo 11cm a medida do raio da bola, seu volume
é igual a
4 3
4
5324
3
Vesfera = .πR ⇒ Vesfera = .π 11 =
≅ 5572cm3
3
3
3
Para você fazer – p. 27
2) Se o volume de uma esfera mede 36π dm³,
calcule a área da secção determinada por
um plano que intersecta a esfera a 2 dm de
distância de seu centro.
Sendo R a medida do raio da esfera, temos
4
36π = .πR 3 ⇒ R 3 = 27 ⇒ R = 3 dm
3
Sendo r a medida do raio da secção, temos
32 = 22 + r 2 → r 2 = 5
Assim, a área da secção é igual a πr 2 = 5π dm 2
Para você fazer – p. 27
3) Mexerica, tangerina, bergamota, mimosa, seja qual
for o nome pelo qual a identificamos, essa deliciosa
fruta é apreciada por grande parte dos brasileiros.
Supondo-se que uma dessas frutas tem o formato
próxima de uma esfera cujo raio mede 3 cm e é
composto por 12 gomos idênticos, calcule o volume
aproximado de um desses gomos. (Utilize π = 3,14).
O volume de cada gomo é aproximadamente igual a
1 4
. .λ.33 = 3π ≅ 9,42cm3
12 3
Área da superfície esférica
Para calcular área da superfície esférica, a
soma de n pirâmides até formar uma esfera,
ou seja:
V p1 + V p 2 + V p 3 + ... + V pn = Vesfera
1
 1
 1

1

 . Ab .R  +  . Ab .R  +  . Ab .R  + ... +  . Ab .R  = Vesfera
3
 3
 3

3

1

n. . Ab .R  = Vesfera
3

1
4
. Ab .R.n = .πR 3
sup erfície esférica
3
3
A
= 4.πR
2
Área da superfície esférica
Exemplo de aplicação
Suponha que tenhamos de colorir três bolas
de isopor cujos raios medem 10cm, 8cm e
6cm. Qual a medida da área total que deverá
ser colorida?
Asup erfície esférica = 4.πR 2 ⇒ Asup erfície esférica = 4.π 10 2 + 4.π 82 + 4.π 6 2
Asup erfície esférica = 4.π 100 + 4.π 64 + 4.π 36 ⇒ Asup erfície esférica = 400.π + 256π + 144.π
Asup erfície esférica = 800πcm 2
Como π ≅ 3,14, a área a ser colorida é aproximadamente igual
a 800.3,14 = 2512cm2
Para você fazer – p 28
1) Determine o volume de uma esfera,
sabendo-se que a área de sua superfície é
igual a 144π cm².
Sendo R a medida do raio da esfera, temos 144π = 4πR 2
R 2 = 6cm
Assim , o volume de esfera é igual a
4 3 4 3
3
Vesfera = πR = π 6 = 288πcm
3
3
Para você fazer – p 28
2) Os volumes de uma esfera, cujo raio mede R, e de um cilindro,
cujo raio da base mede R e cuja altura mede h, são iguais.
a) Determine h em função da
medida do R.
Se os volumes são iguais
4 3
πR = πR 2 h
3
4R
h=
3
b) Calcule a medida da altura
do cilindro, sabendo-se que
o raio da esfera tem medida
9cm.
Se R = 9, temos que
4 R 4.9
h=
=
= 12cm
3
3
Para você fazer – p 28
3) Duas esferas maciças, cujos os raios
medem 4cm e 8cm, são fundidas para
moldar uma única esfera. Calcule a medida
do raio dessa nova esfera.
O volume da nova esfera é igual à soma dos volumes das outras duas.
Sendo R a medida do raio da nova esfera, temos :
4
4
4
4
4 3 4
3
3
3
3
.πR = .πR1 + .πR2 → .πR = .π 8 + .π 43
3
3
3
3
3
3
R 3 = 512 + 64 ∴ R 3 = 576 ∴ R = 3 576 ∴
R = 3 26.32 ∴ R = 43 9cm
Resolução de Atividade
Página 25 e 29