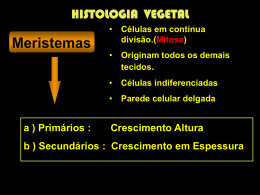
Árvores
Transparências da profa. Renata Galante da II/UFRGS
com permissão
Árvores
• As árvores, diferente das listas, não são estruturas de
dados lineares. São estruturas apropriadas para
realizar uma estrutura hierárquica de objetos.
• São adequadas para representar:
– sistemas de arquivos,
– interfaces gráficas com o usuário (organização dos menus,
por exemplo),
– organização das páginas de um site,
– torneio de tênis (partidas),
– organização hierárquica de cargos ou setores de uma
empresa,
– forma de avaliação de expressões aritméticas, etc.
2
• As árvores, normalmente, são esquematizadas
graficamente como na figura 1, a qual exemplifica o
sistema de arquivos de um dispositivo de
armazenamento.
exemplo de árvore
3
Árvores
A
B
E
C
F
Constituem uma das
estruturas mais importantes
da área de computação,
inclusive em aplicações
D
G
H
I
J
K
4
Árvores
• Relacionamento lógico:
– hierarquia ou subordinação:
– onde um subconjunto dos
componentes é subordinado a outro
A
B
E
C
F
D
G
H
I
J
K
5
Exemplos de aplicações de árvores
Abstração de Composição
BRASIL
RJ
SC
RS
SP
PR
POA CAXIAS GRAMADO CANELA SMARIA TORRES
8
Exemplos de aplicações de árvores
Árvore de derivação - compilador
+
*
a
/
b
c
+
d
e
Expressão aritmética: ( a * b ) + ( c / ( d + e ) )
9
Exemplos de aplicações de árvores
Ordenar valores
200
150
100
350
170
250
500
400
600
Árvore ordenada - esquerda / raiz / direita
10
Terminologia
A
Raiz
B
C
D
11
Terminologia
A
Raiz
B
E
C
F
D
G
H
I
J
K
Sub-árvores
12
Definição de árvore
• Uma árvore enraizada T, ou simplesmente uma
árvore, é um conjunto finito de elementos
denominados nós ou vértices tais que:
– T = 0 é a árvore dita vazia ou
– existe um nó especial r, chamado raiz de T; os restantes
constituem um único conjunto vazio ou são divididos em m
(deve ser maior ou igual a 1) conjuntos distintos não vazios
que são as subárvores de r, cada subárvore a qual é, por
sua vez, uma árvore.
13
Terminologia
Pai
Pai
= mãe
= ascendente
= antecessor
X
Irmão
Filho
= filha
= descendente
= sucessor
Irmão
Filho
= irmã
14
Terminologia
Grau de um nó é igual ao número de sub-árvores do mesmo
Folha ou terminal: Nó com grau igual a zero
Grau de uma árvore
máximo entre os graus
de seus nodos
grau 3
grau 2
A
grau 1
B
E
C
F
D
G
H
I
J
folhas
K
folhas
15
Terminologia
Floresta
disjuntas
X
Y
O
é um conjunto de zero ou mais árvores
M
L
N
Q
P
R
S
A
B
T
E
C
F
D
G
H
I
J
K
16
Terminologia
Caminho seqüência de nós distintos, tal que
existem sempre nós consecutivos que possuam
entre si a relação “é filho de” ou “é pai de”.
A v1
v1 alcança vk e que vk é alcançado por v1
B
E
C
F
D
G
comprimento do
caminho: número de
nós no caminho -1
H
comprimento=3
I
J
K vk
17
Terminologia
Nível de um nó é o número de nós entre ele e a raiz.
Raiz tem nível 1.
A
B
E
C
F
Altura ou
profundidade
nível 1
G
D
nível 2
H
nível 3
de
uma árvore é igual ao
seu maior nível
Altura=4
nível 4
I
J
K
18
Operações sobre árvores
• Dados: árvore A
• Operações básicas:
– criação da árvore
– inserção de um novo nodo
• a raiz
• como folha
• em posição intermediária
– exclusão de um determinado nodo
– acesso a um nodo
A
B
E
C
F
D
G
H
I
J
K
• determinar forma de percorrer a árvore
– destruição da árvore
19
Representação física de árvores
Representação física de árvores
• contigüidade física (usando array)
• encadeamento (com referências)
A
B
E
C
F
D
G
H
I
J
K
21