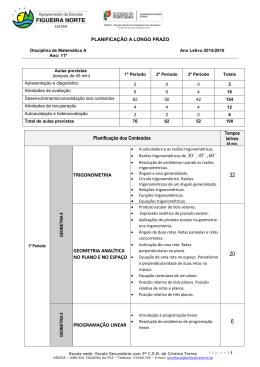
Planificação a médio e longo prazo
Matemática B
11º Ano de escolaridade.
Total de aulas previstas: 193
Ano letivo 2015/2016
Professor responsável: Paulo Sousa
I – O programa
Matemática B do 11º Ano - Página 1 de 5
Primeiro período – 78 aulas
Tema I – Movimentos não lineares. Taxa de variação e funções racionais.
Número de aulas: 43
Conteúdos
- Funções racionais.
Objetivos
Noção de função racional.
Estudo das funções do tipo
1
1
, y 2
y
ax
ax
1
e y
.
a ( x  h) 2
Estudo de algumas funções
racionais recorrendo à
divisão inteira de polinómios.
Simplificação de fracções
racionais.
Equações e inequações
fraccionárias.
 Construir modelos para situações reais utilizando diversos tipos de funções.
 Reconhecer que o mesmo modelo pode representar diferentes situações.
 Analisar os efeitos das mudanças de parâmetros nos gráficos de funções.
 Descrever o comportamento de uma função nos ramos infinitos.
 Resolver equações e inequações fraccionárias.
 Estudar o crescimento (ou decrescimento) da variável dependente em fenómenos
variados.
 Utilizar a tecnologia na aquisição de novos conceitos.
Aplicar os conceitos de taxa média de variação e taxa de variação na resolução de
problemas
- Funções definidas por
ramos.
- Taxa média de variação
num intervalo a, b ; taxa de
variação em x 0 .
Variação e taxa média de
variação num intervalo.
Taxa de variação em x 0
Tema II – Modelos de probabilidades
Número de aulas: 27
Conteúdos
-Introdução ao cálculo
probabilidades
de
-Modelos de Probabilidades
-Aproximações concetuais para
probabilidades
Aproximação
frequencista
de
probabilidade
Definição clássica de probabilidade ou
de Laplace
-Distribuição
probabilidades
- Variável aleatória
Objetivos
 Reconhecer as vantagens em encontrar modelos matemáticos apropriados para
estudar fenómenos aleatórios.
 Compreender as aproximações conceptuais para a probabilidade:
- aproximação frequencista de probabilidade;
-definição clássica ou probabilidade de Laplace.
 Construir modelos de probabilidade em situações simples e usá-los para calcular
a probabilidade de alguns acontecimentos.
de  Reconhecer e dar exemplos de situações em que os modelos de sucessões sejam
adequados.
- Modelo binomial
- Modelo Normal
Número de aulas: 8
Matemática B do 11º Ano - Página 2 de 5
Apresentação (1)
Testes de Avaliação (4)
Auto e heteroavaliação (1)
Atividades Interdisciplinares do PAA (2)
Segundo período – 63 aulas
Tema III - Modelos discretos. Sucessões.
Número de aulas: 28
Conteúdos
- Sucessões.
Conceito de sucessão.
Método Recursivo para
definir uma sucessão.
Sucessões monótonas e
limitadas.
-Progressões aritméticas
e geométricas.
Objetivos
 Usar uma folha de cálculo para trabalhar numérica e graficamente com sucessões.
 Reconhecer e dar exemplos de situações em que os modelos de progressões aritméticas
ou geométricas sejam adequados.
 Distinguir crescimento linear de crescimento exponencial.
 Investigar propriedades de progressões aritméticas e geométricas, numérica, gráfica e
analiticamente.
 Resolver problemas simples usando propriedades de progressões aritméticas e de
progressões geométricas.
Tema IV - Modelos contínuos não lineares
Número de aulas: 28
Conteúdos
- Função exponencial.
- Função logarítmica.
- Equações exponenciais
e logarítmicas
Objetivos
 Reconhecer e dar exemplos de situações em que os modelos exponenciais sejam bons
modelos quer para o observado quer para o esperado.
 Usar as regras das exponenciais e as calculadoras gráficas ou computador para encontrar
valores ou gráficos que respondam a possíveis mudanças nos parâmetros.
 Interpretar uma função e predizer a forma do seu gráfico.
 Descrever as regularidades e diferenças entre os padrões lineares e exponenciais.
 Definir o número e e logaritmo natural.
 Resolver equações simples usando exponenciais e logarítmos (no contexto da resolução
de problemas).
Número de aulas: 7
Testes de Avaliação (4)
Auto e heteroavaliação (1)
Atividades Interdisciplinares do PAA (2)
Terceiro período – 52 aulas
Tema IV - Modelos contínuos não lineares (continuação)
Número de aulas: 8
Conteúdos
- Modelo logístico.
Objetivos
Identificar o modelo logístico.
Tema V - Problemas de optimização.
Aplicações das taxas de variação.
Programação linear, como ferramenta de planeamento e gestão.
Número de aulas: 37
Conteúdos
- Taxas de variação e
Objetivos
 Reconhecer numérica e graficamente a relação entre o sinal da taxa de variação e a
Matemática B do 11º Ano - Página 3 de 5
extremos.
- Programação linear.
monotonia da função.
 Reconhecer a relação entre os zeros da taxa de variação e os extremos de uma função.
 Resolver problemas de aplicações simples envolvendo a determinação de extremos de
funções racionais, exponenciais, logarítmicas e trigonométricas.
 Reconhecer que diferentes situações podem ser descritas pelo mesmo modelo
matemático.
 Resolver numérica e graficamente problemas simples de programação linear.
 Reconhecer o contributo da matemática para a tomada de decisões, assim como as suas
limitações.
Número de aulas: 7
Testes de Avaliação (4)
Auto e heteroavaliação (1)
Atividades Interdisciplinares do PAA (2)
II – A avaliação
Instrumento base – Testes
Seis Instrumentos Base: cinco testes e uma prova comum sendo que em cada período serão
realizados dois Instrumentos Base
Para cada teste e prova comum número de aulas:2
Tipologia de itens
Itens de construção.
Resposta restrita e resposta extensa.
Número:6 a 13.
A resposta aos itens de construção pode envolver, por exemplo, a produção de um
texto com orientação e extensão variáveis, a apresentação de cálculos, justificações
ou de conclusões, de construções geométricas, ou a utilização das potencialidades da
calculadora.
Duração
100 minutos
Critérios gerais de classificação
Todos os testes e prova comum serão corrigidos com base nos Critérios Gerais de Exames em vigor.
Critérios específicos de classificação
Cabe ao professor estabelecer os critérios específicos para cada teste
Instrumento complementar – Ic
Dimensões
Empenho nas tarefas realizadas na aula (35%)
Desempenho das tarefas realizadas na aula (35%)
Desempenho das tarefas propostas, pelo professor ,extra aula (30%)
Critérios gerais/específicos de classificação
A classificação a atribuir em cada dimensão é uma variável qualitativa.
As variáveis qualitativas são: nenhum, insuficiente, suficiente, bom e muito bom.
Matemática B do 11º Ano - Página 4 de 5
A classificação em cada dimensão traduz-se numa classificação quantitativa por aplicação da seguinte conversão:
- Nenhum 0
- Insuficiente 5
- Suficiente 10
- Bom: 15
- Muito bom: 20
A classificação do Instrumento Complementar, com aproximação às décimas, a atribuir a cada aluno é
igual à média pesada das classificações obtidas em cada dimensão.
Classificação final
Primeiro período
Instrumento base - Ib
Avaliação do trabalho do primeiro período
Cp  0,75  Ib  0,25  Ic
Ib  0,5  T1  0,5  T 2
Avaliação final do primeiro período : Cf1  Cp
Classificação arredondada às unidades
Segundo período
Instrumento base - Ib
Avaliação do trabalho do segundo período
Cp  0,75  Ib  0,25  Ic
Ib  0,5  T 3  0,5  T 4
Avaliação final do segundo período : Cf 2  0,6Cp  0,4Cf1
Classificação arredondada às unidades
Terceiro período
Instrumento base - Ib
Avaliação do trabalho do terceiro período
Cp  0,75  Ib  0,25  Ic
Ib  0,4  T 5  0,6  T 6
Avaliação final do terceiro período: Cf 3  0,6  Cf 2  0,4Cp
Classificação arredondada às unidades
IV – Plano anual de atividades
Atividade a desenvolver
Olimpíadas nacionais de matemática.
Tempos letivos disponibilizados
As turmas têm disponíveis dois tempos letivos por período
para atividades interdisciplinares.
Aprovado em reunião de departamento de 17 de setembro de 2015
Matemática B do 11º Ano - Página 5 de 5