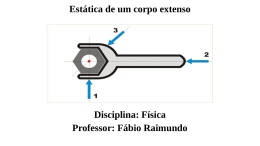
ESTÁTICA
MARCELO ALANO
Corpo extenso
 Corpo extenso: qualquer objeto que pode
girar em torno de seu eixo. (portas, volantes,
régua, etc)
Momento de uma força
(torque)
 Unidade SI: N.m
 Pode-se usar também: N.cm ou Kgf.m
 Lembrando: 1kgf = 9,8 N
Exemplo
 Suponha F1=100N, F2=20N e F3=50N. Em que
sentido vai girar a barra?
O somatório dos momentos de
uma força
Condições de equilíbrio de um
corpo extenso
 Para condições em que o corpo pode girar, as
condições de equilíbrio são:

 equilíbrio de translação:
F  0
 equilíbrio de rotação:
M  0
 Para um ponto material tínhamos apenas:

F  0
Exemplo da apostila
Teorema das Três Forças
 Quando um corpo extenso está em equilíbrio
estático sujeito a três forças não paralelas, as
linhas de ação dessas forças devem passar
por um ponto comum.
 As direções de P e N são
facilmente identificadas,
enquanto F é determinada
pelo teorema.
Centro de gravidade
 Ponto onde podemos considerar aplicado o
peso total do corpo ou sistema.
Centro de gravidade
Centro de gravidade
Centro de massa
 Momento exercido pelo peso: P=Mg
 Equação para calcular o centro de gravidade.
 Centro de gravidade e massa coincidem apenas quando
o corpo está imerso em um campo gravitacional
uniforme.
Centro de massa e
gravitacional
 Centro de gravidade está relacionado ao
momento exercido pela força peso e centro
de massa está relacionado com a força
resultante.
 No nosso caso estamos mais interessados no
centro de gravidade.
Estabilidade do equilíbrio
estático
 Estável: corpo retorna a posição inicial.(a)
 Instável: corpo não retorna a posição inicial.(b)
 Indiferente: corpo é deslocado de sua posição inicial e,
mesmo após ser liberado, não se move.(bola sobre uma
superfície horizontal)
Alavancas
 Barra rígida que pode girar em torno de um
ponto de apoio.
Tipos de alavancas
 Alavanca interfixa: ponto de apoio entre a
potência e a resistência.
Tipos de alavancas
 Alavanca interpotente: força potente entre o
apoio e a resistência.
Tipos de alavancas
 Alavanca inter-resistente: resistência entre o
ponto de apoio e a força potente.
Tipos de alavancas
 O antebraço é uma alavanca interpotente em
que o fulcro está na articulação com o úmero
(osso do cotovelo) e a força potente é exercida
pelo bíceps.
Exercícios:

Competência de área 5: Entender métodos e procedimentos próprios das
ciências naturais e aplicá-los em diferentes contextos.
H17: Relacionar informações apresentadas em diferentes formas de
linguagem e representação usadas nas ciências físicas, químicas ou
biológicas, como texto discursivo,gráficos, tabelas, relações matemáticas ou
linguagem.
Exercícios
Competência de área 6 – Apropriar-se de conhecimentos da física para, em
situações problema, interpretar, avaliar ou planejar intervenções científicotecnológicas.
H20 – Caracterizar causas ou efeitos dos movimentos de partículas, substâncias,
objetos ou corpos celestes.
O que é Estática?
 É a parte da MECÂNICA que estuda o
EQUILÍBRIO das partículas e dos sólidos. O
estudo da ESTÁTICA inicia-se pelo conceito
de FORÇA.
 FORÇA é todo agente capaz de provocar uma
variação de velocidade ou uma deformação
de em um corpo, sendo uma grandeza
vetorial(Caracteres: Módulo; Direção e
Sentido).
OBS sobre FORÇA
 Podemos medir a intensidade de uma FORÇA por
um aparelho denominado DINAMÔMETRO.
 No S.I. a unidade de FORÇA =N(newton)
 FORÇA RESULTANTE ( R ou F r): É a força que
produz o mesmo efeito que todas as forças
aplicadas em um corpo.
 Quando F r = 0 (Nula) ou não existirem forças o
ponto material é dito ISOLADO.
Classificação das FORÇAS
 FORÇAS DE AÇÃO A
DISTÂNCIA.
 São aquelas que atuam
sobre os corpos mesmo
quando não existe o
contato entre eles.
 As forças de ação à
distância atuam numa
região do espaço
denominada de CAMPO.
Ex: a) Força Gravitacional
(Peso) força exercida pela
Terra sobre um corpo de
massa m em proximidades.
Características:
Módulo: P = m . g
Direção: Vertical
Sentido: Para baixo
b)For.Elétrica:(Prótons / elétrons)
c) Força Magnética (Imãs)
Momento de uma Força
É uma grandeza vetorial cuja intensidade é
igual ao produto entre o módulo da força F e a
menor distância d do suporte da força ao ponto
de rotação (O).
Fy
F
d
d
O
O
F

Fx
MF,O = + F y . d = F.d.sen 
MF,O = + F . d (sentido anti - hor.)
MF,O = - F . d (sentido horário).
(No S.I. a unidade é N.m.)
Binário ou Conjugado
 É um sistema construído por duas forças de
intensidades iguais, de mesma direção e de
sentidos opostos, mas cujas linhas de ação estão
separadas por uma distância d (braço) não nula.
 Momento do Binário: M = ± F . D
 A Resultante do Binário é nula. Um corpo
rígido , não sofrerá translação submetido a
um binário e sim movimento de rotação não
uniforme.
Ex:14- Ao extrair uma porca que prende a roda de um carro, um
homem aplica forças de intensidade de 4,0 N com as duas mãos
numa chave de roda, mantendo as mãos a 50 cm uma da outra.
Determine o momento aplicado pelo homem.
Sol:
Dados: F = 4,0 N e d = 50 cm = 0,50 m
O momento do binário vale:
M = F . d = 4,0 . 0,50  M = + 2,0 N. m
F
-F
(+)
Anti-horário
(- )
Horário
Ex:16-
Sol:
Ex:17
Sol:
Equilíbrio de um corpo extenso
 Condições
 1ª - A resultante de todas as forças que agem sobre o
corpo é nula.
 R=0
R x = 0 e R y = 0 .Esta condição faz com que o
corpo não possua movimento de translação.
 2ª - A soma algébrica dos momentos de todas as forças
que atuam no corpo em relação a um ponto é nulo (  M =
0 ). Esta situação faz com que o corpo não tenha
movimento de rotação.
Ex:20
Sol
Ex:24
Sol
Ex: 27-(FGV – SP) Em uma alavanca interfixa, uma
força motriz de 2 unidades equilibra uma
resistência de 50 unidades. O braço da força motriz
mede 2,5 m; o comprimento do braço da
resistência é:
a) 5 m
b) 0,1 m
c) 1 m
d) 125 m
e) n.d.a.
Sol: Alternativa c. ; Dados: F m = 2 u
2,5 m
Fm=2u
e F R = 50 u
x
F R = 50 u
Pela 2ª condição de equilíbrio temos que  M = 0;
então: 2,5 . F m - x . F R = 0
2,5 . 2 = x . 50
x = 0,1 m