Algoritmo de Rastreamento de Raios
MGattass
Perspectiva e tamanhos relativos
MGattass
Perspectiva e tamanhos relativos
MGattass
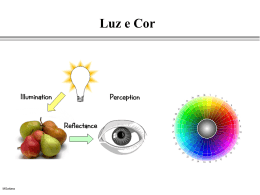
Iluminação e posição
O que está na frente?
A que distância do apoio?
MGattass
Sombra
MGattass
Oclusão
MGattass
Gradiente de textura
Proposto no século XX!
MGattass
Efeitos Passivos
– Inerentes a aparência do mundo externo
– Independem dos nossos olhos
– Fotografias parecem 3D
MGattass
Camera obscura
Plymouth, UK
Camera Obscura - San Francisco
The Camera Obscura at the Cliff House is one of several remaining
camera obscuras in the world. The device is an ancient precursor to
modern photography, and well worth a visit, especially if you haven't
previously visited a camera obscura.
MGattass
Pintores
Canaletto (Giovanni Antonio Canal) (1697-1768).
Dois enfoques: Raios
ye
Traçado de Raios
ze
xe
zo
Para cada pixel da tela
xo
Defina um raio
Para cada objeto da cena
Calcule o objeto visível
Para cada luz da cena
Lance um raio
Para cada objeto da cena
Teste se o objeto faz sombra
Calcule sua iluminação
yo
Complexidade maior que O(num. de pixels  num. de objetos2)
Dois enfoques: ZBuffer
Calcule a cor de cada vertice
Projete cada triângulo
Projete os vértices no plano de projeção
Rasterize o triângulo gerandoo os fragmentos que vão para cada pixel
Aqueles fragmentos que estiverem a frente dos framentos já depositados
recebem nova cor e a profundidade do pixel é atualizada.
A Câmara “Pinhole” e seu modelo
centro de
projeção
plano de
projeção
eixo
óptico
raios
MGattass
eixos do
plano de
projeção
Traçado de Raios
Luz
ye
ze eye
Câmara
Objetos
xe
yo
xo
zo
MGattass
Iluminação
Pixel
(RGB)
Algoritmo básico
Luz
ye
ze
Câmara
xe
Iluminação
Objetos
Para cada pixel da tela;
Lance uma raio;
Para cada objeto da cena
Calcule a interseção do raio com este o objeto;
Armazene a interseção mais próxima;
Se o raio interceptou algum objeto
Calcule a contribuição das luzes neste ponto;
Pinte o pixel com esta cor;
MGattass
Definição de uma câmera
Projeção cônica
plano de projeção
centro de projeção
centro
óptico
o
janela
hp (pixels)
h (metros)
eixo eye
óptico
centro de
projeção
janela
o
wp (pixels)
w (metros* )
w
MGattass
(*) metros ou outra unidade de comprimento
wp
hp
h
Abertura de uma câmera
fovy1
fovy2
h
df1
MGattass
df2
 fovy 
h
 tan

2d f
 2 
 fovy 
h  2d f tan

 2 
Eixos de uma câmera
v
ye
eixo vertical
eixo óptico
eye
ye janela
xe
l (left)
eixo horizontal
hp (pixels)
h
u
t (top)
r (right)
ze
o
b (bottom)
MGattass
wp (pixels)
w
xe
Parâmetros de funções do OpenGL
void glPerspective(GLdouble fovy,GLdouble aspect,GLdouble near_,GLdouble far_);
w
ye
ze
aspect = w/h
fovy
h
xe
ze
f
(far)
void glViewport(GLint x0, GLint y0,
GLsizei width, GLsizei height );
v
height
n
(near)
MGattass
ye
y0
o1
width
x0
u
Parâmetros intrínsecos (do OpenGL)
parte 2 – Câmera mais geral
void glFrustum(
GLdouble left, GLdouble right, GLdouble bottom, GLdouble top,
GLdouble near_, GLdouble far_ );
ye
v
ze
near
far
xe
near
xe
left right
ze
MGattass
u
Parâmetros internos ou intrínsecos
Primários:
n = plano próximo
df  n
f = plano distante
 fovy 
h  2d f tan

 2 
wp  hp pixels
fovy = campo de visão
MGattass
Derivados:
w
wp
hp
h
Posicionamento da câmera
(parâmetros externos ou extrínsecos)
eye
= centro óptico
center = ponto de visada,
up
= direção para cima
y0
vista lateral
up
eye
center
up
eye
fovy
center
x0
z0
Coordenadas dos
Objetos
near
far
MGattass
Calculo do sistema do olho - xe ye ze
up
eye
dados:
eye, center, up
view = center - eye
ze 
y0
center
1
e ye ce nte r
e ye ce nte r
up
x0
eye
z0
view
y0
center
x0
z0
MGattass
ze
Calculo do sistema do olho - xe ye ze
vup
xe
eye
ze
xe 
1
up z e 
up z e
view
y0
center
ye
up
x0
xe
eye
z0
xe
view
ye
y0
center
ze
up
x0
eye
z0
MGattass
center
ze
y e  z e  xe
Um modelo de câmera
d
raio : p(t )  o  td
yo
xo
zo
MGattass
o  eye
d  p xy  eye
Lançamento de Raios
h pixels na altura
v
x
u( x ) 
w
wp
y
v( y ) 
h
hp
h-1
pxy
y
p xy  o1  u( x)uˆ  v( y)vˆ
2
1
o10
1
2
3
x
w-1
u
w pixels na base
MGattass
x
y
p xy  o1  w
xˆ e  h yˆ e
wp
hp
Canto inferior esquerdo da janela no plano near (ou far)
ye
xe
eye
ze
h
w
o1  eye  d f zˆ e  yˆ e  xˆ e
2
2
plano near

a
yˆ e
2
o1
y0
canto inferior
esquerdo
x
y
p xy  o1  w xˆ e  h yˆ e
wp
hp
x0
z0
 y 1
 x 1
d  d f zˆ e  h   yˆ e  w
 xˆ e
h

w

2
2
p
p




MGattass
Resultando
d
raio : p(t )  o  td
yo
o  eye
xo
zo
MGattass
 y 1
 x 1


d  d f zˆ e  h
 yˆ e  w
 xˆ e
h

w

2
2
p
p




Tipo Abstrato de Dados: Camera em C
struct _Camera {
/* Definição da câmera */
Vector eye, center, up;
float fovy;
float n,f;
int
wp,hp;
/* Parametros derivados */
float df;
float w,h;
Vector xe,ye,ze;
};
typedef struct _Camera
Camera;
Camera* camCreate( Vector eye, Vector at, Vector up,
double fovy, double _near, double _far, int wp, int hp
);
Ray camGetRay( Camera camera, double x, double y );
MGattass
Objeto câmera
Inicialização (pré-processamento):
Dados: fovy, wp, hp, n, f, eye, center, up
df  n
ze 
 fovy 
h  2d f tan

2


1
e ye ce nte r
e ye ce nte r
xe 
w
wp
hp
h
1
up z e 
up z e
y e  z e  xe 
Lançamento de raios: o + td
Dados: x, y
o  eye
MGattass
 y 1
 x 1
d  d f zˆ e  h   yˆ e  w
 xˆ e
h

w

2
2
p
p




Modelagem dos Objetos
Implícita:
Por fronteira:
p
p c  r
p3
dados:
centro c
raio r
MGattass
p2
p1
Superfícies implícitas em grades Cartesianas
•
Seja f(x,y,z), uma função amostrada em R3
y
f(x,y,z)
R
a
x
Objetivo:
– Visualizar
z
uma isosuperfície
f(x,y,z) = a.
S
definida
por
Classificação do Voxel
Voxel
opacidade
1.0
Branco
(1,1,1)
Osso
Músculo
Vermelho
(1,0,0)
Gordura
Amarelo
(1,1,0)
ar
cor
0
valor
1.0
Interseção de um raio com uma esfera
Raio: p(t )  o  td
Esfera :
o
d
p(ti )  c  r 2
2
o  ti d  c  r
2
ti
2
o  c  tid o  c  tid  r 2
d  d ti2  2d  (o  c) ti  o  c o  c  r 2   0
a ti2  b ti  c  0
MGattass
 b  b 2  4ac
t
2a
Objeto esfera: métodos (dados o, d, c, r )
Interseção:
a  d d
se ti > 0 :
b  2d  (o  c)
c  o  c o  c  r 2
se   b2  4ac  0
pi  p(ti )  o  tid
Normal:
pi
b 
t1 
2a
b 
t2 
2a
MGattass
ti  min(t1 , t2 )
nˆ i
c
1
pi  c
nˆ i 
pi  c
Interseção com o plano do triângulo
Raio: p(t )  o  td
Plano:
p(ti )  p1  n  0
o  tid  p1  n  0
tid  n  o  p1  n  0
ti
MGattass
nˆ 
o

p1  o   n

dn
p 2  p1  p 3  p 2 
p 2  p1  p 3  p 2 
p3
n
d
p(ti )
p1
pi  p(ti )  o  tid
p2
Ponto interno a triângulo
p3
n  v12  v 23
v23
v31
p2
int
pi
v12
p1
MGattass
p iext




n  v12  (pint
 p1 )  0
i
n  v12  (piext  p1 )  0
Coordenadas baricêntricas
A1  nˆ  v 23  (pi  p 2 ) / 2
A2  nˆ  v 31  (pi  p3 ) / 2
nˆ  unitv12  v31 
A3  nˆ  v12  (pi  p1 ) / 2
p3
AT  A1  A2  A3
v31
nˆ
A1
A2
p
L1  A1 / AT
v23
int
i
L2  A2 / AT
A3
p1
L3  A3 / AT
v12
p
MGattass
ext
i
p2
pi é interior se L1, L2 e L3 [0..1]
Coordenadas baricêntricas como
funções interpolantes
 xi 
 x1 
 x2 
 x3 
 
 
 
 
 yi   L1  y1   L2  y2   L3  y3 
z 
z 
z 
z 
i
1
2
 
 
 
 3
p3
A2
p1
A1
pi
L1
A3
1
p2
L3
MGattass
L1  L2  L3  1
L2
1
1
Interpolação de cor e coordenada de textura
através das coordenadas baricêntricas
c3 u3
p3
A2
p1
c1 u1
 ri 
 r1 
 r2 
 r3 
 
 
 
 
 gi   L1  g1   L2  g 2   L3  g 3 
b 
b 
b 
b 
 i
 1
 2
 3
A1
pi
ou:
A3
p2
c2 u2
MGattass
ui 
u3 
u1 
u2 
   L1    L2    L3  
v1 
v2 
vi 
v3 
Forma otimizada de calculo
o
p i  o  ti d
pi  L1p1  L2p2  L3p3
d
p3
n
p(ti )
p1
pi  o  tid  (1  L2  L3 )1p1  L2p2  L3p3
Tomas Möller, Ben Trumbore
Fast, Minimum Storage Ray/Triangle Intersection
MGattass
p2
Forma otimizada de cálculo
o
d
p3
n
p(ti )
p1
o  tid  (1  L2  L3 )1 p1  L2p2  L3p3
 tid  L2 (p2  p1 )  L3 (p3  p1 )  o  p1
 ti 
 
 d (p 2  p1 ) (p 3  p1 ) L2   o  p1 
L 
 3
Ax  b
MGattass
p2
Caixa alinhada com os eixos
d=(dx, dy, dz)
o
ti
(xmin, ymin, zmin)
y
z
(xmax, ymax, zmax)
x
d x  0  x  xmin
d y  0  y  ymax
d z  0  z  zmax
MGattass
Motivação: Uma cena simples
Camera:
eye = (100,40,40), center = (0,0,0), up=(0,1,0), fov=90º, near = 30, far=230,
w=230, h=230.
Esfera:
c = (0,20,0), r = 25, cor azul = (0,0,1)
Caixas alinhadas com os eixos:
p0 = (-80,-50,-50), p1 = (50,-45,50) e cor amarela = (0.7,0.7,0)
p0 = (-80,-50,-60), p1 = (50,50,-50) e cor amarela = (0.7,0.7,0)
Luz Pontual:
Posição=(60,120,40) e intensidade RGB l=(0.8,0.8,0.8)
MGattass
O que conseguiriamos se simplesmente
atribuissemos aos pixels a cor dos objetos?
MGattass
Área aparente
energia
luminosa
I
2
i  lumens / m
A
I (lumens)
A
energia
luminosa

I (lumens)
A
A 
cos 
'
MGattass
I
2
i '  cos  lumens / m
A
Modelo de reflexão de superfíces
Lambertianas
luz
incidente
luz
incidente
luz
incidente
1. Reflete igualmente em todas as direções
2. A intensidade é proporcional ao co-seno
MGattass
Componente de reflexão difusa
cos 
1
nˆ
Lˆ

- /2
pi
 I r   l r k dr cos 
  

 I g    l g k dg cos 
 I   l k cos 
 b   b db

MGattass
0
/2
a
Outras maneiras de se escrever:
 I r   l r k dr cos 
  

 I g    l g k dg cos 
 I   l k cos 
 b   b db

 I r   lr k dr
 
 I g    l g k dg
 I   l k
 b   b db
nˆ  Lˆ   l k 
l

ˆ
ˆ
nˆ  L   l k nˆ  L   l
l
nˆ  Lˆ   l k 

r
dr
g
dg
b db
  k dr 
  
ˆ ˆ
g    k dg  n  L
 k 
b 
 db 
r
 
Eq. 1
I, l, k  [0 ,1 ]
MGattass
Luz difusa mais ambiente:
 I r   lr   k dr 
     
 I g    l g    k dg  nˆ  Lˆ
 I  l  k 
 b   b   db 
 
 I r   I ar   k dr   lr   k dr 
         
 I g    I ag    k dg    l g    k dg  nˆ  Lˆ
 I   I  k  l  k 
 b   ab   db   b   db 
 
MGattass
Componente de reflexão especular
rˆ
nˆ
Lˆ
a
vˆ
Brilho
rˆ  vˆ n
n=1
n=4
n=8
-1
MGattass
-0,5
n




I
l
k
cos
a
 r
r
sr


 
n
  l g k sg cosa  
Ig 

n 
I 



l
k
cos
a
 b  especular  b sb

0
0,5
1
a
Eq.2
I, l, k  [0 ,1 ]
Reflexão especular
 I r   I ar   k dr   l r   k dr 
 l r   k sr 
         
   
n
ˆ
ˆ
ˆ
ˆ


I

I

k

l

k
n

L

l

k
r

v
 g   ag   dg   g   dg 
 g   sg 
 I   I  k  l  k 
l  k 
b
ab
db
b
db
         
 b   sb 
 
MGattass
Reflexão especular
nˆ
rˆ
a vˆ
Lˆ
pi
MGattass
luz
refletida
Cálculo da reflexão de um vetor sobre outros
h
Lˆ
nˆ
ˆ  nˆ )nˆ
Ln  (L
h
Ln
rˆ
h  Ln  L
rˆ  Ln  h


ˆ n
ˆ
ˆ n
ˆ L
rˆ  2 L
MGattass
Distribuição da luz direta sobre um ponto
Lˆ
rˆ
nˆ
vˆ
pi
Ambient
Diffuse
C  Camb  Cluz k dif 
MGattass
 
Specular
n
ˆ
nˆ  L  Cluz k s rˆ  vˆ 
Modelo de várias luzes
  lr   k dr 

 I r   I ar   k dr 
 lr   k sr 


     
   
   
n
ˆ   l    k rˆ  vˆ  
 I g    I ag    k dg      l g    k dg  nˆ  L
g
sg
luzes
 l   k 

 I  I  k 
l  k 
 b   ab   db 
 b   sb 
  b   db 

 
ˆ  nˆ )nˆ  L
ˆ
rˆ  2(L
para cada fonte de luz
rˆr  2( vˆ  nˆ )nˆ  vˆ
uma reflexão apenas
  l r   k dr 
 I r   I ar   k dr 
 l r   k sr 

     
   
   
ˆ
ˆ
 I g    I ag    k dg      l g    k dg  nˆ  L   l g    k sg  rˆr  L
 I   I   k  luzes   l   k 
l  k 
b
db
 b   ab   db 




 b   sb 

 
MGattass


n




Sombra
Raio de sombra: p(t )  pi  t rˆs
rˆs
pi
A luz não chega a superfíce
MGattass
Modelo de várias luzes e sombra
  l r   k dr 
 I r   I ar   k dr 
 lr   k sr 
   
     
   
ˆ
ˆ
 I g    I ag    k dg    f s   l g    k dg  nˆ  L   l g    k sg  rˆr  L
 I   I   k  luzes   l   k 
l  k 
 b   ab   db 
 b   sb 
  b   db 
 
se sombra
0
fs  
1 caso contrário
MGattass


n




Fontes de luz especiais: Onidirecional
MGattass
Fonte: Mauricio Hofmam
Fontes de luz especiais: Direcional
MGattass
Fonte: Mauricio Hofmam
Fontes de luz especiais: Farolete
MGattass
Fonte: Mauricio Hofmam
Uma revisão
MGattass
Reflexão de outros objetos
Raio refletido: p(t )  pi  t rˆr
nˆ
rˆr

vˆ

pi
Superfície especular
MGattass
Transparência
Raio refratado: p(t )  pi  t rˆt
nˆ
h1
rˆt
MGattass
vˆ
1
Objeto transparente
pi
2
h2
lei de Snell
h1 sin  2

h 2 sin 1
Cálculo do Raio Refratado
vt  ( vˆ  nˆ )nˆ  vˆ
nˆ
vˆ
sin i  vt
vt
i v n
tˆ
pi
t
 nˆ
hi
sin  t  sin  i
ht
cos  t  1  sin 2  t
rˆt
ˆt  1 v t
vt
rt  sin t tˆ  cost (nˆ )
MGattass
Raio refratado: p(t )  pi  t rˆt
Advertência: Refração não é simples!
MGattass
Iluminação considerando superfícies
refletoras e objetos transparentes
  lr   k dr 
  I r (rr ) 
 I r   I ar   k dr 
 lr   k sr 
 I r (rt ) 
   

     
   




n
ˆ
ˆ
 I g    I ag    k dg    f s   l g    k dg  nˆ  L   l g    k sg  rˆr  L   k  I g (rr )   (1  o) I g (rt ) 
  I (r ) 
 I   I   k  luzes   l   k 
l  k 
 I (r ) 
b
db
b
sb
 b   ab   db 








 b t 

  b r 
 

redução da
reflexão
MGattass

redução da
transparência
Natureza recursiva do algoritmo de
Rastreamento de Raios
R2
R1
L2
T1
L1
L3
T2
R3
L1
R1
L2
T1
L3
R2
MGattass
R3
T2
Resultado de curso
MGattass
Alunos de CGI98
Algoritmo de traçado de raios
selecione o centro de projeção(eye) e uma janela no plano de projeção
for (cada pixel da tela)
{
determine o raio ray que vai do centro de projeção ao pixel;
pixel = trace ( ray, 1);
}
}
Color trace (Scene scene, Vector3d eye, Vector3d ray, int depth)
{
determine a interseção mais próxima com um objeto
if (intercepta objeto)
{
calcule a normal no ponto de interseção
return ( shade ( scene, object, ray, point, normal, depth));
}
return BACKGROUND;
}
MGattass
Color shade (Scene scene, Object object, Vector3D ray,
Vector3D point, Vector3D normal, int depth)
{
color = termo ambiente do material do objeto ;
for (cada luz) {
L = vetor unitário na direção de point para a posição da luz;
if (L • normal>0) {
if (a luz não for bloqueada no ponto) {
color += componente difusa (Eq.1) + componente especular (Eq.2)
} }
if (depth >= maxDepth) return color;
if (objeto é refletor) {
rRay = raio na direção de reflexão;
rColor = trace(scene, point, rRay, depth+1);
reduza rColor pelo coeficente de reflexão especular e some a color; }
return color;
}
Texturas
v
v
v
1.0
1.0
1.0
0
1.0 u
0
1.0 u
0
1.0 u
Texturas 2D = Imagens onde o domínio é u, v [0,1]×[0,1]  R2
MGattass
Sistemas de coordenada de textura na caixa
face x=xmax
(0,0)
v
u
(1,1)
(0,0)
u
y  ymin
ymax  ymin
z  z min
v
z max  z min
u
y
MGattass
(0,0)
v
v
z
u
x
Sistema de coordenada de textura na esfera
z   cos
x   sin  cos
y   sin  sin 
z


y

tan 
x
u  1 
v  1
MGattass
tan  y / x


x2  y2
z
i
i  v(h  1)
j  u( w  1)
j
Sistema de coordenada de textura no triângulo
v
3 (u3,v3)
v3
2
v1 = v2
1
(u1,v1)
u1= u3
MGattass
u2
u
(u2,v2)
Textura no triângulo e coordenadas baricêntricas
p3
A3  nˆ  v12  (pi  p1 ) / 2
v31
nˆ
A2
p1
A1  nˆ  v 23  (pi  p 2 ) / 2
A2  nˆ  v 31  (pi  p3 ) / 2
A1
v23
L1  A1 / AT
L2  A2 / AT
L3  A3 / AT
p int
i
A3
L3  1  ( L1  L2 )
v12
p2
ui 
u3 
u1 
u2 

L

L

L
  1  2   3 
v1 
v2 
vi 
v3 
MGattass
AT  A1  A2  A3
Textura
MGattass
Texturas de rugosidade (bump textures) e
Texturas de deslocamentos (displacement mapping)
nˆ
nˆ '  nˆ   ( , )
MGattass
Pertubar aleatóriamente
as normais dos objetos
Pertubar aleatóriamente
as posições dos pontos
z=x
z
x
(1,1)
y
v
(0,0)
MGattass
u z=-x
y=x
y=-x
Textura ambiente (environment maps)
face dos raios x>y e x>z
yx
u
2x
zx
v
2x
Tratamento anti-alias
a
dxdy
sub-pixels
pixel
dx, dy = variáveis randômicas
MGattass
•Lance um raio para cada sub-pixel
•Faça uma média dos valores obtidos
Anti-alias
pixel
(a) original
MGattass
pixel
(b) uniforme
pixel
(c) “jittered”
Refinamento Progresivo
MGattass
amostragem inicial
primeira subdivisão
segunda subdivisão
subdivisão final
pixels
sendo visitados
pixels
já visitados
Radiosidade e Ray Tracing
standard raytracing
global illumination
MGattass
Klaus Mueller, Stony Brook University, Computer Science (CSE 564)
Todays State of the Art
- Some Snapshots
Feb 3rd, 2003
Afrigraph 2003
Aceleracao do RT
• Cálculos mais eficientes
• Uso de uma Kd Tree
MGattass
Classificação do Voxel
Voxel
opacidade
1.0
Branco
(1,1,1)
Osso
Músculo
Vermelho
(1,0,0)
Gordura
Amarelo
(1,1,0)
ar
cor
0
valor
1.0
Lançamento dos Raios
plano de
visualização
y
volume dos
raios
x
z
volume dos
slices
raio
Partição dos Raios
x
ta
z
voxel
tb
y
amostra
t=min(x,y,z)
Iluminação de um voxel
 
ˆ
C  Camb  Cluz kdif  nˆ  L
N
Gel A
Gel B
L
N  V (X )
Estimativa do vetor normal
f x, y, z 
N
f x, y, z 






 f xi 1 , y j , zk   f xi 1 , y j , zk  / 2x ,


f xi , y j , zk    f xi , y j 1 , zk   f xi , y j 1 , zk  / 2y ,
 






f
x
,
y
,
z

f
x
,
y
,
z
/
2

z
,
i
j k 1
 i j k 1

1a ordem
2a ordem
Influência de um Voxel
r=0
g=0
b=0
r0
g0
b0
r1
g1
b1
a0
a1
a0
r = a 0 r0
g = a0 g0
b = a0 b0
a  a0
r = a0 r0+1a0  a1 r1
g = a0 g0+1a0  a1 g1
b = a0 b0+1a0  a1 b1
a  a0 +1a0  a1
Composição no raio
a out  a in  (1  a in )a
C out  C  (1  a )a C
in
in
ray
Cin
C  C out a out
Cout
Interpolação
x,i
(xa, ya, za)
x
i a 
 Dx
y
j a 
 Dy
za 

k
 Dz
z,k
y,j
xa % Dx
x
Dx
ya % Dy
y
Dy
za % Dz
z
Dz
Interpolação no voxel
v( x, y, z )  1  x 1  y 1  z vi , j ,k 
vi +1,j,k +1
vi,j,k +1
vi+1,j+1,k+1
vi,j +1,k +1
vi+1,j,k
y x
vi,j,k
v z
vi+1,j+1,k
vi,j+1,k
x 1  y 1  z vi1, j ,k 
1  x  y 1  z vi, j 1,k 
x  y 1  z vi1, j 1,k 
1  x 1  y z vi, j ,k 1 
x 1  y z vi1, j ,k 1 
1  x  y z vi, j 1,k 1 
x  y z vi1, j 1,k 1
Etapa de Composição
• Para cada raio:
gera amostras de cor C (pi) e opacidades a(pi)
• reamostragem dos dados dos voxels, em k amostras
igualmente espaçadas
• Processo de acumulação
I= t Ib +(1-t)I0
I0 = cor do objeto
Ib = cor do fundo
I = cor resultante
t = coeficiente de transparência
ezy= (y)z +(-z)y +cyz
Tripod
z
exy exz ezy
y
exy= (y)x + (-x)y +cxy
(x0+x,y0 +y,z0 +z)
(x0,y0,z0)
x
exz= (z)x + (-x)z +cxz
+

+
-
-


+
-
Valor inicial e incremento
(1/2,1/2,1/2) x++
exy= (y)x + (-x)y +cxy
(y-x)/2
y
exz= (z)x + (-x)z +cxz
(z-x)/2
z
ezy= (y)z +(-z)y +cyz
(y-z)/2
y++
z++
x
x
z
y
Caminhamento discreto
Bresenham
Cohen
Efeito da amostragem
Bresenham
Tripod
Partição celular
Volume
de dados
Voxel
Partição
uma amostra no meio da partição
marcador da partição
Partição na grade
nx  (ib  ia )  1
z
n y  ( jb  ja )  1
(ia ,ja ,0) nz  (kb  ka )  1
tzi= ta
tyi
t x  (t xf  t xi ) nx
t y  (t yf  t yi ) n y
tyf=tb tzf
(ib ,Ny ,kb)
t z  (t zf  t zi ) nz
y
Partição celular: algoritmo
Dados: txi,tyi,tzi, txf,tyf,tzf, nx,ny,nz
dtx = txf/nx; dty = tyf/ny; dtz = tzf/nz;
tx=txi; ty=tyi; tz=tzi;
t1 = min(tx,ty,tz) e w é o eixo do mínimo
n=nx+ny+nz;
while ( n > 0 )
tw += dtw;
n--;
t2 = min(tx,ty,tz) e w é o eixo do mínimo
Sample ((t1+t2)/2);
t1=t2;
Otimizações
• Velocidade
– Refinamento progressivo
– Terminação adaptativa do raio
– Estruturas Hieráquicas
• Qualidade da imagem
– aumento do número de amostra no raio
– lançamento de mais raios
– melhora esquema de interpolação
Refinamento Progresivo
amostragem inicial
primeira subdivisão
segunda subdivisão
subdivisão final
pixels sendo visitados
pixels já visitados
Refinamento Progressivo: Exemplo
2x2
4x4
8x8
16x16
32x32
64x64
128x128
256x256