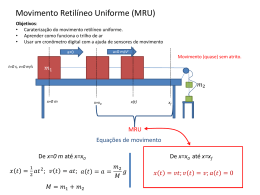
UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE
ESCOLA DE CIÊNCIAS E TECNOLOGIA
Princípios e Fenômenos da Mecânica
Professor: Humberto
EXPERIMENTO Nº 4 – CONSERVAÇÃO DA ENERGIA MECÂNICA
Discentes:
Camila de Oliveira Silva (2009028716)
Gabriel Araújo
(2009029224)
José Henrique T. D. Góis (2009032110)
Thiago Mateus B. da Silva(2009030605)
Turma 2 A
NATAL
23/04/2010
Objetivo
O presente relatório tem como finalidade apresentar resultados obtidos na prática laboratorial
do dia dezenove de abril, com a turma 2 A de Princípios e Fenômenos da Mecânica, juntamente com
professores e monitores de laboratório, no horário de 10h 50 min às 12 h 30 min. Nesse experimento,
nosso objetivo foi verificar a conservação de energia mecânica de um objeto(carrinho) que se movia
em movimento retilíneo uniformemente variado (MRUV) sobre um trilho de ar plano e sem atrito, com
inclinações de 1° e 5°, nessa ordem.
Introdução Teórica
A vida que conhecemos requer basicamente energia, pois todo e qualquer fenômeno que
acontece na natureza necessita dela para ocorrer. Diariamente, vemos noticiários sobre a cotação do
petróleo e sabemos que este é o fator primordial de desenvolvimento mundial. E uma das notícias mais
recentes é a polêmica sobre a construção da Usina Hidrelétrica do Belo Monte, que teria capacidade de
“gerar” a energia necessária para cobrir a demanda de toda a região norte do Brasil.
Mas como uma usina gera energia? Essa é uma resposta que a Física pode explicar: quando a
água passa pelas turbinas localizadas nas barragens da usina, a força das águas gera sua rotação,
produzindo velocidade (energia cinética), que é adquirida graças à força represada das águas (energia
potencial gravitacional). Ou seja, não acontece uma geração, e sim uma transformação. Essa é
basicamente uma explicação da Primeira Lei da Termodinâmica, onde: “A energia pode se transformar
de uma forma em outra, mas não pode ser criada ou destruída”.
Reconhecendo que um tipo de energia pode ser transformado em outros e tendo aprendido, em
sala de aula, o Princípio de Conservação de Energia Mecânica, podemos fazer a seguinte afirmação:
“Em um sistema isolado, onde apenas forças conservativas causam variações de energia, a
energia cinética e a energia potencial podem variar, porém, a energia total do sistema, ou seja, a
energia mecânica, é constante.
∆𝐸𝑚𝑒𝑐 = ∆K + ∆U = 0
A Energia mecânica é a soma da energia potencial U com a energia cinética K. Para o nosso
experimento, cuja energia potencial é somente gravitacional, a energia mecânica é a soma da energia
cinética com a energia potencial gravitacional. Isto é:
𝐸𝑚𝑒𝑐 = K + 𝑈𝑔
A energia associada à velocidade é denominada energia cinética K (citada acima). Esta é igual
à metade do módulo do produto do quadrado da velocidade pela massa de uma partícula.
𝑚𝑣 2
𝐾=
2
Porém, a energia cinética, por si só, não é conservativa, pois um corpo pode estar acelerado.
Pode-se definir, então, essa variação de energia cinética em relação ao tempo como a potência
transferida P de/a uma partícula por uma força 𝐹 . Assim:
𝑃 = 𝐹𝑣 =
𝑡2
𝑑𝐾
𝑑𝑡
𝑡2
𝑃 𝑑𝑡 =
𝑡1
𝑡2
𝐹𝑣 𝑑𝑡 =
𝑡2
𝑡2
𝑡1
𝑡2
𝑃 𝑑𝑡 =
𝑡1
𝐹
𝑡1
𝑡2
𝑑𝑟
𝑑𝑡 = 𝐾2 − 𝐾1
𝑑𝑡
𝑟2
𝑃 𝑑𝑡 =
𝑡1
𝑑𝐾
𝑑𝑡
𝑑𝑡
𝐹 𝑑𝑟 = ∆𝐾
𝑟1
À integral da potência entre os tempos 𝑡1 e 𝑡2 , dá-se o nome de trabalho (W).
𝑊 = 𝐹 . ∆𝑑
Para a força peso:
𝑊𝑝𝑒𝑠𝑜 = 𝑚𝑔ℎ2 − 𝑚𝑔ℎ1 → 𝐸𝑝𝑔 = 𝑚𝑔ℎ
Agora, tratando-se de duas configurações distintas dos objetos do sistema, sabendo que a
variação de energia potencial de um corpo ∆U é definida como o negativo do trabalho realizado por ele
(-W), e que a variação de energia cinética ∆K é o trabalho realizado W, podemos fazer a seguinte
relação:
∆K = W
∆U = -W
∆K = -∆U
𝐾2 – 𝐾1 = -(𝑈2 – 𝑈1 )
𝐾2 + 𝑈2 = 𝐾1 + 𝑈1
𝐸2 = 𝐸1
Tudo o que foi provado foi a conservação da energia, como diz o princípio que citamos.
A partir dessas teorias, ficamos aptos a realizar os cálculos e entender o problema.
Material Utilizado
Para a realização do experimento sobre Conservação da Energia Mecânica, foram utilizados
alguns materiais, a saber:
Trilho de ar inclinável;
Gerador de corrente de ar;
Dois sensores ópticos;
Computador com um software para captar os eventos dos sensores;
Um carrinho;
Trena;
 Dinamômetro.
O trilho de ar inclinável é um aparelho que reduz consideravelmente o atrito entre o carrinho
(objeto que se movimenta) e o trilho, permitindo a obtenção de dados próximos aos ideais. Do trilho
sai um fluxo de ar (regulável), que é fornecido pelo gerador de corrente de ar. O trilho é feito de
metal, é oco e tem diversos orifícios.
Figura 1 : Trilho de ar inclinável.
Figura 2: Gerador de fluxo de ar
O intervalo de tempo gasto pelo carrinho para se deslocar entre dois pontos é medido pelos
sensores ópticos. No momento em que o primeiro sensor sofre uma interferência no fluxo, um
cronômetro é iniciado. O cronômetro para de contar o tempo no instante em que o carrinho passa pelo
segundo sensor (segunda interferência).
Figura 3: Sensor óptico
O carrinho é o objeto que vai se mover pelo trilho, ele possui dez pares de franjas, cada uma com
18 mm de largura. Os tempos são marcados quando cada franja passa pelo sensor.
Figura 4: Carrinho
O software contido no computador recebe os intervalos dos movimentos do carrinho em cada
franja que passa pelos sensores. É com esses dados que podemos realizar os cálculos para encontrar o
valor da energia mecânica do sistema.
Figura 5: Interface do temporizador
O dinamômetro é o aparelho que mede a força (em Newtons) de um objeto.
Figura 6: Dinamômetro
Procedimento Experimental
O procedimento desse laboratório foi utilizar o trilho inclinado, em 1º e 5º, respectivamente,
para que dessa forma, o carrinho solto percorresse o trilho sem que utilizássemos força para isso.
Ativamos o software e colhemos dados do tempo, como também medimos a altura com que o sensor 1
e o sensor 2 faz com a vertical. Vale acrescentar que o carrinho possui 10 pares de franjas. Sendo
assim, teríamos que escolher apenas o tempo em que o mesmo par de franjas passasse pelos dois
sensores, com a finalidade de provar que a variação de energia cinética e potencial para um mesmo
ponto pode mudar com o tempo, porém a variação de energia mecânica do sistema é constante.
Para o ângulo de 1º, os dados são:
Para o ângulo de 5º, os dados são:
∆𝒕𝟏 (segundos)
∆𝒕𝟐 (segundos)
∆𝑺(metros)
𝒉𝟏 (metros)
𝒉𝟐 (metros)
0,150
0,074
0,018
0,193
0,191
∆𝒕𝟏 (segundos)
∆𝒕𝟐 (segundos)
∆𝑺(metros)
𝒉𝟏 (metros)
𝒉𝟐 (metros)
0,034
0,018
0,018
0,249
0,213
Feita essa etapa, medimos a massa do carrinho utilizando um dinamômetro:
𝑚𝑐𝑎𝑟𝑟𝑖𝑛 ℎ𝑜 = 0,255 kg
Resultados e discussão
(a) Considerando desprezível o atrito entre o carrinho e o trilho, podemos esperar que a energia
mecânica do carrinho seja conservada, ou seja, E1 = E2. Preencha a tabela 11 e verifique se a
energia foi realmente conservada (podemos dizer que houve conservação quando δE < 7%).
Na parte superior do carrinho há dez pares de franjas, cada uma com 18 mm de largura. Não
precisamos utilizar os dados de tempo de todas elas; basta apenas de uma. Porém, se utilizarmos o
tempo em que a quarta franja passa no sensor 1, tempos que utilizar o tempo em que essa mesma franja
passa no sensor 2, por exemplo.
O desenho abaixo mostra o plano inclinado em 1º, bem como h1 e h2 as alturas no sensor 1 e no
sensor 2, respectivamente:
Com o plano inclinado em α = 1°, escolhemos os intervalos de tempo da sexta franja, que é o
seguinte:
𝛥𝑡1 (segundos)
0,150
𝛥𝑡2 (segundos)
0,074
Como a distância entre cada par de franjas é 0,018 m, podemos calcular a velocidade media do
carrinho nesse pequeno deslocamento.
𝑣1 =
0,018 𝑚
𝑣2 =
0,150 𝑠
𝑣1 = 0,120 m/s
0,018 𝑚
0,074 𝑠
𝑣2 = 0,243 m/s
Considerando as seguintes afirmações:
𝐸𝑛 : Energia Mecânica no ponto 𝑃𝑛 ;
𝑈𝑛 : Energia Potencial Gravitacional no ponto 𝑃𝑛 ;
𝐾𝑛 : Energia Cinética no ponto 𝑃𝑛 ;
Podemos resolver da seguinte forma:
𝐸1 = 𝐸2
𝐸1 = 𝑈1 + 𝐾1
𝐸2 = 𝑈2 + 𝐾2
𝑈1 + 𝐾1 = 𝑈2 + 𝐾2
1
1
2
2
m.g. ℎ1 + . m.𝑣12 = m.g. ℎ2 + . m.𝑣22
Onde:
𝑈1 = 𝑚. 𝑔. ℎ1
𝑈1 = 0,255 . 9,8 . 0,193
𝑈1 = 0,4823 J
𝑈2 = 𝑚. 𝑔. ℎ2
𝑈2 = 0,255 . 9,8 . 0,191
𝑈2 = 0,4773 J
1
𝐾1 = 𝑚 . 𝑣12
2
1
𝐾1 = . 0,255 . (0,120)2
2
𝐾1 = 0,0018 J
1
𝐾2 = 𝑚 . 𝑣12
2
1
𝐾2 = .0,255 . (0,243)2
2
𝐾2 = 0,0075 J
O erro é calculado da seguinte maneira:
δE =
𝐸1 + 𝐸2
𝐸1
𝐸1 = 0,4823 + 0,0018
𝐸1 = 0,4841 J
𝐸2 = 0,4773 + 0,0075
𝐸2 = 0,4848 J
δE =
0,4841 – 0,4848
0,4841
δE = 0,001 x 100% = 0,1%
Portanto, dado os resultados experimentais, podemos preencher a tabela (para o ângulo de 1º):
𝑣1 (m/s)
0,120
𝑣2 (m/s)
0,243
𝐾1 (J)
0,0018
𝑈1 (J)
0,4823
𝐾2 (J)
0,0075
𝑈2 (J)
0,4773
𝐸1 (J)
0,4841
𝐸2 (J)
0,4848
δE(%)
0,1
O desenho abaixo corresponde à experiência para uma inclinação de 5°:
Nesse caso, o sensor marcou os seguintes intervalos:
𝛥𝑡1 = 0,034 s
𝛥𝑡2 = 0,018 s
Como o espaço de uma franja corresponde a 0,018 m, as velocidades correspondentes são:
𝑣1 =
0,018 𝑚
𝑣2 =
0,034 𝑠
𝑣1 = 0,529 m/s
0,018 𝑚
0,018 𝑠
𝑣2 = 1,000 m/s
De modo análogo à inclinação de 1°, encontramos a energia do carrinho quando o plano tinha uma
inclinação de 5° da mesma forma:
𝐸1 = 𝐸2
𝐸1 = 𝑈1 + 𝐾1
𝐸2 = 𝑈2 + 𝐾2
𝑈1 + 𝐾1 = 𝑈2 + 𝐾2
1
1
2
2
m.g. ℎ1 + . m.𝑣12 = m.g. ℎ2 + . m.𝑣22
1
𝑈1 = 𝑚. 𝑔. ℎ1
𝑈1 = 0,255 . 9,8 . 0,249
𝑈1 = 0,6223 J
𝐾1 = 𝑚 . 𝑣12
𝑈2 = 𝑚. 𝑔. ℎ2
𝑈2 = 0,255 . 9,8 . 0,213
𝑈2 = 0,5323 J
𝐾2 = 𝑚 . 𝑣12
2
1
𝐾1 = 0,255 . (0,529)2
2
𝐾1 = 0,0357 J
1
2
1
𝐾2 = 0,255 . (1,000)2
2
𝐾2 = 0,1275 J
𝐸1 = 𝑈1 + 𝐾1
𝐸1 = 0,6223 + 0,0357
𝐸1 = 0,6580 J
𝐸2 = 𝑈1 + 𝐾1
𝐸2 = 0,5323 + 0,1275
𝐸2 = 0,6598 J
Como a fórmula para calcular o erro é:
δE =
𝐸1 − 𝐸2
𝐸1
Então, fazemos:
δE =
0,6580− 0,6598
0,6580
δE = 0,002 x 100% = 0,2%
Portanto, com esses resultados podemos preencher a tabela:
𝑣1 (m/s)
0,529
𝑣2 (m/s)
1,000
𝐾1 (J)
0,0357
𝑈1 (J)
0,6223
𝐾2 (J)
0,1275
𝑈2 (J)
0,5323
𝐸1 (J)
0,6580
𝐸2 (J)
0,6598
δE(%)
0,2
Dessa forma, como os erros para ambos os ângulos foi menor que 7%, podemos dizer que a
energia foi conservada. Mas também podemos inferir que esses erros normalmente são encontrados em
experiências, visto que diferenças na precisão do programa, contato com a bancada do experimento,
forma como foi solto o carrinho, resistência do ar no laboratório, entre outros, podem ter causado essa
diferença.
Conclusão
Para a realização desse experimento, o trilho foi posicionado com ângulos de 1º e 5º,
respectivamente. O carrinho foi solto, e o software marcou os intervalos de cada franja de 18 mm, para
ambos os sensores. Medimos as respectivas alturas do sensor 1 e do sensor 2, como também colhemos
dados em que uma mesma franja passou por estes. Baseando-se nas equações do Princípio de
Conservação da Energia Mecânica, obtivemos os dados tanto para o sensor 1 como para o 2. Para o
ângulo de 1º, obtivemos uma energia mecânica de 0,4841 J no sensor 1 e de 0,4848 J no sensor 2. O
erro neste caso foi de 0,1%. Para o ângulo de 5º, a energia mecânica calculada foi de 0,6580 J no
sensor 1 e 0,6598 no sensor 2, gerando um erro de 0,2%.
Explicamos que o erro em um experimento sempre pode existir, já que não estamos lidando com
um ambiente ideal (sem atrito, sem resistência do ar, umidade, etc). Diferenças na precisão do
programa, forma como o carrinho foi solto, resistência do ar no laboratório, contato com a bancada,
respiração de quem estava perto no momento do procedimento, entre muitas outras causas, podem ser
a razão da existência desses erros experimentais. Podemos inferir também que o erro foi maior no
ângulo de 5º, pois que se utilizarmos as Leis de Newton (calcular através de F = m.a), veremos que a
componente da força que age é 𝑃𝑥 , ou seja, P.senα. Observamos que o seno dos ângulos é maior com o
aumento do ângulo. Então, isso significa que a componente 𝑃𝑥 no ângulo de 5º é maior do que no
ângulo de 1º, pois 𝑃𝑥 em 5º é maior do que 𝑃𝑥 em 1º, causando um maior erro.
De qualquer forma, os erros foram mínimos, o que torna conclusivo que a energia mecânica se
conservou nesse experimento. Provamos em um ambiente real que a energia é conservativa se a
energia mecânica de um objeto, em intervalos diferentes, for a mesma. Isso significa que a energia
cinética e a energia potencial do corpo podem variar com o decorrer do tempo, mas a energia mecânica
do sistema não.
Bibliografia
HALLIDAY; RESNICK. Fundamentos de Física. 8ª Ed. V1. LTC. RJ 2008.
Trilho de ar, sensores, gerador de fluxo de ar
Disponíveis em <http://www.fitalab.com.br/acess_aulas_didaticas/dinamometro.jpg> (Acesso em 22
de abril 2010).
Dinamômetro.
Disponível em
<http://www.cidepe.com.br/resources/multimidia/images/upload/produtos/g1241806509_EQ238.jpg>
<http://pt.wikipedia.org/wiki/Dinam%C3%B4metro> (Acesso em 22 abril de 2010).
Interface do temporizador. Disponível em < http://www.cidepe.com.br/openGal/1403/> (Acesso em
22 de abril de 2010).