UNIVERSIDADE FEDERAL DE MINAS GERAIS
PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
PLANEJAMENTO E ANÁLISE DE EXPERIMENTOS
Professor:
Prof. D. Felipe Campelo
Ensaio da Influência de componente
harmônico, nos circuitos de tensão e
corrente de Medidores de Energia.
Júlio Cesar de Oliveira
PPGEE-UFMG
BELO HORIZONTE – MG
2012
Conteúdo
i.
Introdução
ii.
Descrição do Problema
iii. Descrição do Planejamento
iv. Análise dos Resultados
v.
Conclusão
i. Introdução
“Influência de componente harmônico nos
circuitos de tensão e corrente em Medidores
de Energia”.
O ensaio foi realizado conforme orientações de Norma Específica, modelo abaixo.
3
i. Introdução
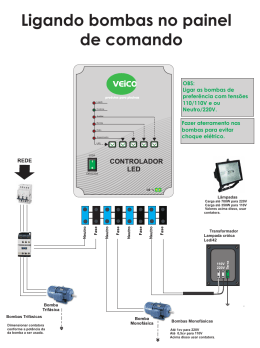
Conexões dos equipamentos utilizados durante o ensaio
4
ii. Descrição do Problema
Problema: “Influência de componente harmônico nos circuitos de tensão e corrente”.
Objetivo: Medir os erros sob condições, com e sem Tensões Harmônicas e verificar
se estão dentro da tolerância garantida de 2,00%.
Condições de Teste no meio Ambiente:
Temperatura: (23 ± 2) °C
Umidade relativa do ar: (50 ± 10) %
5
ii.Descrição do Problema
DESENVOLVIMENTO
Foram aplicados Tensões Un de 120V e 220V e 0,5*Imáx (senoidais) com cos φ = 1, aos
elementos de tensão e corrente do medidor, respectivamente, e determinado o
erro nesta condição.
Em seguida foram aplicadas formas de onda com tensão do quinto harmônico de
0,1*Un e corrente do quinto harmônico de 0,4*Inom, conforme Norma específica,
em cada um dos equipamentos, e determinado o erro nesta condição.
Tais procedimentos foram realizados três vezes para cada medidor, a fim de se obter
uma amostra de valores medidos, para a determinação do erro percentual,
conforme norma da RTM anexo à Portaria 431/2007 – Item B.11.
6
ii. Descrição do Problema
PROCEDIMENTO
Foram feitos warm-up de 05 pulsos da energização do
medidor, até o início da contabilização do tempo de
ensaio, em 120 segundos.
Os procedimentos acima foram realizados na frequência
60 Hz.
7
ii. Descrição do Problema
Estratégia Escolhida: Planejamento DOE fatorial 2^3, com 3 replicações .
Teste de Hipótese : yijk = µ + τi + βj + γk+(τβ)ij + (τγ)ik + (βγ)jk + (τβγ)ijk+ϵijkl
𝑯𝟎 : 𝝁𝑯𝟏𝟐𝟎= 𝝁𝟐𝟐𝟎= 𝝁𝑯𝟓 𝑵Ã𝑶= 𝝁𝑯𝟓 𝑺𝑰𝑴= 𝝁𝑬𝑵𝑬𝑹𝑮.𝑫𝑰𝑹𝑬𝑻𝑨= 𝝁𝑬𝑵𝑬𝑹𝑮.𝑹𝑬𝑽𝑬𝑹𝑺𝑨=𝟎
𝑯𝟏 : 𝝁𝑯𝟏𝟐𝟎 ≠ 𝝁𝟐𝟐𝟎≠ 𝝁𝑯𝟓 𝑵Ã𝑶≠ 𝝁𝑯𝟓 𝑺𝑰𝑴≠ 𝝁𝑬𝑵𝑬𝑹𝑮.𝑫𝑰𝑹𝑬𝑻𝑨≠ 𝝁𝑬𝑵𝑬𝑹𝑮.𝑹𝑬𝑽𝑬𝑹𝑺𝑨≠𝟎
8
Teste de Hipóteses: yijk = µ + τi + βj + γk+(τβ)ij + (τγ)ik + (βγ)jk + (τβγ)ijk+ϵijkl
ϵijkl
{
i = 1, . . . , a
j = 1, . . . , b
k =1, . . . , c
l = 1, . . . , n
As hipóteses de teste foram definidas como sendo:
1) H0: τ1 = τ2 = . . . = τa = 0 (sem efeito no fator principal
Tensão H1-120V ou 220V);
H1: Pelo menos um τi≠ 0.
2) H0: β1 = β2 = . . . = βb = 0 (sem efeito no fator principal
Tensão H5 Harmônico, inserido ou não);
H1: Pelo menos um βj ≠ 0.
3) H0: γ1 = γ2 = . . . = γc = 0 (sem efeito no fator principal Energia);
H1: Pelo menos algum γk ≠ 0.
4) H0: (τβ)11 = (τβ)12 = . . . = (τβ)ab = 0 (sem efeito na interação dos fatores);
H1: Pelo menos algum (τβ)ij ≠ 0.
9
iii. Descrição do
Planejamento
Equipamentos utilizados
Padrão de Potência Elétrica Fluke 6100A / 6101A - Pat: 138761 - Série: 915152211
CERTIFICADO DE CALIBRAÇÃO: 282-12B
Dados Coletados: Próximo Slide
10
iv. Análise dos Resultados
Dados Coletados conforme planilha abaixo, que foram aleatorizadas no Minitab:
RunOrder
CenterPt
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Blocks
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Tensão H1
1 120V
1 120V
1 220V
1 220V
1 220V
1 120V
1 120V
1 220V
1 220V
1 220V
1 120V
1 120V
1 120V
1 120V
1 120V
1 220V
1 220V
1 220V
1 120V
1 120V
1 220V
1 220V
1 220V
1 120V
Tensão H5
Não
Não
Sim
Sim
Sim
Não
Sim
Não
Não
Não
Sim
Sim
Sim
Sim
Sim
Não
Não
Não
Não
Não
Sim
Sim
Sim
Não
Energia
Direta
Direta
Reversa
Reversa
Reversa
Direta
Reversa
Direta
Direta
Direta
Reversa
Reversa
Direta
Direta
Direta
Reversa
Reversa
Reversa
Reversa
Reversa
Direta
Direta
Direta
Reversa
Erro
0,173
0,3
-0,09
0,045
0,045
0,217
0,399
0,091
0,091
0,091
0,099
0,093
0,171
0,198
0,297
-0,045
-0,045
-0,045
0,023
0,058
0,045
0,18
0,18
0,015
11
iv. Análise dos Resultados
Análise dos Dados Coletados: Minitab
Ferramentas:
• Create Factorial Design
• Diplay Design
• Analyse Factorial Design
• Factorial Plots
Full Factorial Design
Factors: 3
Base Design:
Runs: 24
Replicates:
Blocks: 1
2; 8
3
12
iv. Análise dos Resultados
Teste F para nível de significância 𝐝𝐞 𝟗𝟓% 𝐜𝐨𝐦 𝜶 = 0,05:
Analysis of Variance for Erro
Source
DF
SS
Tensão H1
1 0,093750
Tensão H5
1 0,022694
Energia
1 0,091513
Tensão H1*Tensão H5
1 0,001734
Tensão H5*Energia
1 0,011354
Tensão H1*Energia
1 0,000864
Tensão H1*Tensão H5*Energia 1 0,011094
Error
16 0,103690
Total
23 0,336692
MS
F
0,093750 14,47
0,022694 3,50
0,091513 14,12
0,001734 0,27
0,011354 1,75
0,000864 0,13
0,011094 1,71
0,006481
P
0,002
0,080
0,002
0,612
0,204
0,720
0,209
13
iv. Análise dos Resultados
Neste gráfico de tendência, vemos que os resultados dos erros permaneceram
estáveis dentro durante a fase de testes, pois eles envolvem a curva mediana, e não
apresenta efeitos quadráticos.
14
iv. Análise dos Resultados
O gráfico de probabilidade normal demonstra que os pontos que estiverem mais
afastados da reta são significantes para a resposta, no caso abaixo é possível
visualizar que os pontos A e C são significantes, ou seja Tensão H1 e Energia.
15
iv. Análise dos Resultados
O gráfico de Pareto, abaixo, mostra que todos os efeitos que ultrapassam a linha no
valor de 2,120 são significantes com 95% de confiança, desse modo pode-se
confirmar que todos os fatores são A e C significantes para resposta.
16
iv. Análise dos Resultados
Efeitos Principais
No gráfico abaixo, pode-se observar que temos valores médios de Tensão H1 e Energia
como maiores efeitos principais sobre os erros médios, pois a linha que conecta as
respostas médias para o nível baixo e o nível alto tem inclinação maior comparada a
tensão H5.
17
iv. Análise dos Resultados
Efeitos de interação vemos que não existem efeitos de interações, uma vez que as
retas são praticamente paralelas sem se cruzarem.
18
iv. Análise dos Resultados
No gráfico da probabilidade normal versus resíduos , a normalidade é identificada
quando os dados tendem a uma reta, o que ocorre neste caso. No Gráfico dos valores
Residuais ajustados uma certa homocedascidade.
19
iv. Análise dos Resultados
No gráfico de probabilidade de erro medidos, vemos que as mesmas se encontram
dentro de um intervalo de confiança de 95%.
20
Conclusão
One-Sample T: Erro; CenterPt
Test of mu = 2 vs not = 2
Variable N Mean
StDev SE Mean
95% CI
T
P
Erro
24 0,107750 0,120991 0,024697 (0,056660; 0,158840) -76,62 0,000
CenterPt 24 1,00000 0,00000 0,00000 ( 1,00000; 1,00000)
*
*
21
Conclusão
Conforme gráfico abaixo, vemos que este gráfico representa o Contorno do Erro
de segunda ordem, com as condições abaixo:
22
Conclusão
23
Conclusão
24
Conclusão
Portanto, segundo os dados e gráficos apresentados pelo MINITAB, pode-se dizer
que o maior efeito para é o “ A e C-”, ou seja, quando os fatores são utilizados nos
seguintes níveis: H1 nível mínimo e Energia nível Direta, Portanto conforme vimos o
equipamento testado, manteve-se dentro do requisito da norma.
25
Bibliografia
Montgomery D. Design Analisys of Experiments – John Wiley
Montgomey Engineering Applied Statistics and Probability for Engineer.
Notas de Aula do Prof. Dr. Felipe Campelo - PPGEE - UFMG