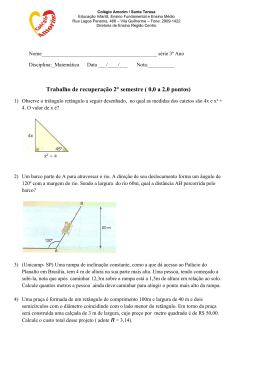
SEMELHANÇAS
TRIÂNGULOS
Aplicações
DE
UM TOPÓGRAFO PRECISA MAPEAR UMA CERTA
ÁREA ONDE HÁ UM RIO E UMA ESTRADA. PARA
ISSO, ELE PRECISA DESCOBRIR A LARGURA DO
RIO E A DISTÂNCIA DA ESTRADA ATÉ A
MARGEM DO RIO. APÓS REALIZAR TODAS AS
MEDIDAS, COMEÇOU A CHOVER E SUA
PRANCHETA FICOU COMPLETAMENTE MOLHADA,
FAZENDO COM QUE ALGUNS DE SEUS DADOS
SE APAGASSEM. VEJA O ESQUEMA ABAIXO E
AJUDE O TOPÓGRAFO A RECUPERAR SEUS
DADOS.
26 m
Largura do rio
y
α
13 m
Distância da
margem do rio
à estrada.
30 m
β
x
60°
15 m
Sa= soma dos ângulos internos de um triãngulo.
Sa= 180
Sa= 60° + 90° + β
β = 180° - 90° - 60°
β= 30°
Considerando α = β, pois são ângulos OPV (opostos
pelo vértice), temos que:
tg β = 15/x
tg 30°= 15/x
√3/3 = 15/x
x .√3= 45
x = 45/√3
x =15√3
x≈26 m
tg α = 26/y
tg 30° = 26/y
y ≈ 44,2
R: A largura do rio é de
aproximadamente 44,2 m e a distância
da margem do rio até a estrada é
cerca de 26 m.
MARCELO PRECISA COMPRAR UMA CERTA
METRAGEM DE CORDA PARA HASTEAR DUAS
BANDEIRAS. PORÉM, ELE NÃO SABE O
TAMANHO DAS HASTE ONDE AS BANDEIRAS
FICARIAM. SABENDO A SOMBRA QUE A
HASTE MENOR PROJETA É DE 10 M E DA
MAIOR É DE 15 M, QUAL É O TAMANHO DAS
RESPECTIVAS HASTES? VEJA O ESQUEMA
ABAIXO:
α
h
60°
15 m
10 m
3. SOU
UM PEDREIRO E PRECISO
CONSTRUIR UMA RAMPA PARA O ACESSO
À DEFICIENTES FÍSICOS EM UMA
LOJA.SABENDO QUE A RAMPA TEM
DE EXTENSÃO E
3M
5M
DE ALTURA, A QUE
DISTÂNCIA DA LOJA EU DEVEREI
COMEÇAR A FAZER A RAMPA?
5
3
x
Utiliza-se o teorema de Pitágoras:
A² + B² = C²
5² +X² = 3²
25 + X² = 9
25 – 9 = X²
X² = 16
X = 4
R: A rampa deverá ser construída a 4
m de distância da loja