SISTEMAS
Prof. Marcelo de Oliveira Rosa
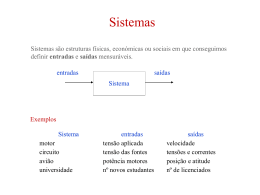
Sistemas
Definição
 Entidade que
manipula um ou vários sinais
(entrada), produzindo um ou vários sinais (saída)
 Composição:
 Sinais de entrada
 Sistema (propriamente dito)
Sistema
Sinais de
saída
 Sinais de saída
Sinais de
entrada

Sistemas

Definição
 Terminologias adicionais
 Entradas 
Excitação  x(t)
 Saídas  Resposta  y(t)
 Matematicamente
 h{} é uma operação
realizada sobre uma função x(t)
para produzir uma função y(t)
x(t)
h{}
y(t)
Sistemas

Diagrama de Blocos
 Somador
 w(t)
= x(t) – y(t) + z(t)
z(t)
+
z(t)
x(t)
+
x(t)
+
+
+
+
w(t)
z(t)
w(t)
y(t)
x(t)
+
Σ
-
-
y(t)
y(t)
w(t)
Sistemas

Diagrama de Blocos
 Amplificador
 y(t)
= K x(t)
x(t)
x(t)
x(t)
K
y(t)
y(t)
K
K
y(t)
Sistemas

Diagramas de Blocos
 Integrador/diferenciador
 y(t)

= ∫ x(τ) dτ
(de – ∞ até t)
x(t)
 y(t)
∫
y(t)
d/dt
y(t)
= dx(t)/dt
x(t)
Sistemas

Exemplos
 Navegação de
barcos
 Entradas



Empuxo da hélice
Posição do leme
Direção e velocidade da correnteza
 Saída


Direção do barco
Velocidade do barco
 Sistema


Dinâmica dos fluidos
Equações do movimento de corpos
Sistemas

Exemplos
 Suspensão automotiva
 Entradas

Distância entre roda e solo
 Saídas

Distância entre chassi e chão
 Sistema

Equações dinâmicas de movimento
 fator de amortecimento
 energia elástica.
Sistemas

Exemplos
 Ponte
 Entrada


Direção do vento
Velocidade do vento
 Saída

Deslocamento da ponte
 Sistema


Dinâmica dos fluidos
Interação entre fluido e estrutura
 exemplo: Ponte Tacoma
Sistemas

Exemplos
 Corpo
humano
 Entradas

Dose de medicamento
 Saídas

Concentração da dose no corpo
 Sistema


Equação farmacocinética do medicamento
Equação de infusão e eliminação do medicamento
Sistemas

Modelagem de sistemas
 Definir equações que
“ligam” as entradas às saídas
 Geralmente equações integro-diferenciais

Equações diferenciais ordinárias (por exemplo)
 Há sistemas complexos demais para modelagem
detalhada


Uso de aproximações e simplificações
Tratamento estocástico
 Exemplos
Sistemas

Propriedades
 Resposta com entrada nula
 Saída do sistema para entrada x(t)
= zero
 Condições de contorno não-nulas

Caracteriza efeito da energia inicial do sistema na saída
 Resposta com condições
iniciais nulas
 Saída do sistema para entrada x(t)
≠ zero
 Condições de contorno nulas

Geralmente energia inicial do sistema é nula
Sistemas

Propriedades
 Resposta total
≠
Respostas com entrada nula + Respostas com
condições inicias nulas
 Existe situações de igualdade
 EDOs


lineares a coeficientes constantes
Solução homogênea
Solução particular
Sistemas

Propriedades
 Homogeneidade
 Um sistema é homogêneo quando sua saída é sempre
proporcional à sua entrada

Condições iniciais nulas
x(t )  y(t )  ax(t)  ay(t)
h{}
h{}
Sistemas

Propriedades
 Aditividade
 Duas entradas (x1(t) e x2(t))
produzem respostas y1(t) e
y2(t), respectivamente, para um sistema H.

Condições iniciais nulas
O
sistema é aditivo se x3(t) [= x1(t) + x2(t)] produzir
resposta y3(t) [= y1(t) + y2(t)]
h{}
x1 ( t ) 
y1 ( t ) 

h{}
x 2 ( t )  y 2 ( t )
h{}
x1 ( t )  x 2 ( t )  y1 ( t )  y 2 ( t )
Sistemas

Propriedades
 Linearidade
 Combinação de homogeneidade e aditividade.
 Princípio da superposição.


“Dividir para conquistar”
Método comum a classe de sistemas (lineares)
h{}
x1 ( t ) 
y1 ( t ) 

h{}
x 2 ( t )  y 2 ( t )
h{}
ax1 ( t )  bx 2 ( t ) 
ay1 ( t )  by 2 ( t )
Sistemas

Propriedades
 Linearidade
 Como aplicar o

método a sistemas não-lineares?
Processo de linearização
 Linearização



Equações diferenciais não-lineares exatas transformadas
em equações diferenciais lineares aproximadas
Adição de restrições para aproximação
Exemplo clássico:
 Pêndulo para pequenos ângulos
Sistemas

Propriedades
 Invariância no tempo
 Um sistema é invariante no tempo se uma entrada x(t)
atrasada/adiantada t0 instantes de tempo produz uma
saída atrasada/ adiantada t0 instantes de tempo

Condições iniciais nulas
x(t)  y(t)  x(t  t 0 )  y(t  t 0 )
h{}
h{}
Sistemas

Propriedades
 Linearidade e
Invariância no tempo
 LTI

“Linear and time-invariant system”
 Combinação de linearidade e invariância no tempo
 Classe específica de sistemas


Análise será baseada em relações em excitações específicas
Uso de convolução
Sistemas

Propriedades
 Estabilidade
O
sistema não “explode”
 Critério BIBO

Para qualquer excitação limitada, o sistema produzirá
sempre respostas limitadas
x(t)  A  y(t)  h{x(t)}  B

Condições iniciais nulas
Sistemas

Propriedades
 Estabilidade
 Para um sistema descrito por uma EDO
linear com
coeficientes constantes, a solução homogênea (sem
excitação)



Descrita por combinação linear de exponenciais complexas
 Exponenciais complexas = autofunções
Se Re{autovalores} ≥ zero  sistema instável
Se Re{autovalores} < zero  sistema estável
 Caso particular importante
Sistemas

Propriedades
 Causalidade
 Um sistema é causal
se ele apresenta resposta somente
durante ou após a aplicação de alguma excitação.
 Sistema não-antecipatório
x(t )  0, t  t 0  y(t )  0, t  t 0

Condições iniciais nulas
Sistemas

Propriedades
 Causalidade
 Processamento tempo-real
 Não-causal  processamento off-line
 Causal

Impossibilidade de aplicações em tempo real, pois análise
depende do “futuro”.
Sistemas

Propriedades
 Causalidade
 Exemplo:
Mercado de ações e filtro média-móvel.
Sistemas

Propriedades
 Memória
 Um sistema com
memória depende das excitações em
instantes anteriores ou posteriores, além da
excitação no instante atual.

Também chamado sistema dinâmico
 Um sistema sem
memória depende apenas da excitação
no instante atual

Também chamado sistema estático
Sistemas

Propriedades
 Reversibilidade/Inversibilidade
 Um sistema é
inversível se excitações singulares
produzem respostas singulares
y(t )  h{x(t )}  x(t )  h 1{y(t )}

Condições iniciais nulas
 Sistema inverso “anula”
completamente os efeitos do
sistema direto.

Idéia de função bijetora
Sistemas

Convolução
 Estado atual:
 Sistemas descritos por EDOs


Solução completa  soluções particular + homogênea
Solução homogênea  combinação linear de autofunções
 Questão:
 Podemos analisar o sistema sem considerar excitações
e respostas?
Sistemas

Convolução
 Princípio
básico
 Excitação

Combinação linear de sinais “elementares”
 Sistema específico


Sistemas lineares e invariantes no tempo (LTI)
Uso do princípio de sobreposição
 Resposta

 Sinal
Combinação linear dos efeitos produzidos pelos sinais
“elementares”
elementar  sinal impulso  δ(t)
Sistemas

Convolução
 Sistema original
 F(y, y’, y’’,

..., y(n-1), y(n)) = G(x, x’, x’’, ..., x(m-1), x(m))
y = y(t) e x = x(t)
 Resposta ao
 A(h,

impulso  h(t)
h’, h’’, ..., h(n-1), h(n)) = B(δ, δ’, δ’’, ..., δ(m-1), δ(m))
h = h(t) e δ = δ(t)
Sistemas

Convolução
 Obtenção da
resposta ao impulso  h(t)
h(t)  hh(t)
 Características da solução particular
 Encontre solução homogênea de


Derive h(t) até a n-ésima derivada e aplique no lado
esquerdo da EDO: deve haver correspondência com todas
as derivadas de δ(t) até m-ésima derivada
 Para t = zero
Combinação linear de h(t) e suas derivadas = zero
 Para t ≠ zero
 Garantia de solução homogênea “vingar”
Sistemas

Convolução
 Obtenção da
resposta ao impulso  h(t)
 n>m

hh(t) u(t)
 n=m

hh(t) u(t) + Kδ δ(t)
 n<m

hh(t) u(t) + [K(m-n)u(m-n)(t) + K(m-n-1)u(m-n-1)(t) + ... +
K1u1(t) + K0u0(t)]
 u0(t) = δ(t), u1(t) = δ’(t), ...
Sistemas

Convolução
 Resposta ao
impulso
 Descrição do sistema para qualquer excitação

Apenas para sistemas lineares e invariantes no tempo!
 Como obter resposta dado h(t) e excitação?
Sistemas

Convolução
 Decomposição de x(t)
 Tp
em soma de pulsos
 duração dos pulsos
Sistemas

Convolução
 Decomposição de x(t)
em soma de pulsos
 Combinação linear de pulsos deslocados no tempo.
 
 t  nTp 

  x (nTp ) rect

T
n



p



x (t )   
 t  nTp 
1

  Tp x (nTp ) rect

T
T
n


p
p



pulso retangular unitário
Sistemas

Convolução
 Pelo princípio da superposição...
 Válido para sistemas lineares e


invariantes no tempo
Lembre-se do exemplos dos filtros RC, RL, RLC, LC
x(t) = pulso unitário  y(t) = hp(t)
y( t ) 

 T x(nT ) h
n  
p
p
p
( t  nTp )
Sistemas

Convolução
 Exemplo
 Excitação 
senóide amortecida
 Sistema  filtro RC
Sistemas

Convolução
 Exemplo
 Excitação 
senóide amortecida
 Sistema  filtro RC
Sistemas

Convolução
 Considerando o
limite Tpτ
 Excitação

x(t )   d x() δ(t  )  x(t )  δ(t )


Qualquer sinal = combinação linear de δ(t)
 Resposta

y(t )   d x() h(t  )  x(t )  h(t )


Integral de convolução
Sistemas

Convolução
 Diagrama de
 y(t)
blocos
= h(t) * x(t)
h(t)
x(t)
 Reforçando
 h(t)
 resposta ao impulso do sistema
y(t)
Sistemas

Propriedades da Convolução

y(t )  x(t )  h(t )   x() h(t  )d

 Em
relação à variável τ
 x(τ) é
mantido é mantida fixa
 h(t – τ) é revertida e deslocada t instante de tempo


Reflexão  h(–τ)
Atraso no tempo  h(–(τ – t))
Sistemas

Propriedades da Convolução
 Visualização do processo
 Para cada t
“fixo”, calculamos a integral (–∞ a +∞)
Sistemas

Propriedades da Convolução
 Convolução entre dois
pulsos unitários
Sistemas

Propriedades da Convolução
 Amostragem do
impulso
x(t) * A δ(t  t 0 )  A x(t  t 0 )
 Comutativa
x(t )  y(t )  y(t )  x(t )
 Distributiva
x(t )  y(t )  z(t )  x(t )  y(t )  x(t )  z(t )
Sistemas

Propriedades da Convolução
 Associativa
x(t ) * y(t )  z(t )  x(t )  y(t ) z(t )
x(t)
y(t)
z(t)
w(t)
x(t)
y(t)
z(t)
w(t)
Sistemas

Propriedades da Convolução
 Distributiva
x(t )  y(t )  z(t )  x(t )  y(t )  x(t )  z(t )
x(t)
y(t)+z(t)
w(t)
y(t)
+
+
x(t)
+
z(t)
w(t)
Sistemas

Propriedades da Convolução
 Se y(t)
= x(t)*h(t)
 Diferenciação
y' (t )  x' (t )  h(t )  x(t )  h' (t )
 Área
Área de y(t)  Área de x(t)  Área de h(t)
 Escala
y(at)  a x(at)  h(at)
Sistemas

Propriedades da Convolução
 Estabilidade
 Se x(t) é
limitado
x(t )  B
 Então

y(t )  x(t )  h(t )  B h() d

 Um sistema é estável ser sua resposta ao impulso for
absolutamente integrável

Existência da convolução
Sistemas

Propriedades da Convolução
 Causalidade
 Um sistema linear e invariante no tempo é causal
h(t )  0, t  0


Sistema não-antecipatório
Convolução em tempo-real
se
Sistemas

Propriedades da Convolução
 Memória
 Um sistema linear e invariante no tempo é estático se:
h(t )  0, t  0

Sistema sem memória
Sistemas

Diagrama de Blocos
 Genericamente
N
M
n 0
m 0
(n )
(m)
a
y
(
t
)

b
x
 n
 m (t)
 Sistema linear e invariante no tempo
 Pode ser representado por convolução
Sistemas

Diagrama de Blocos
 Usando
integradores (forma direta I):
bn
x(t)
+
1/an
+
y(t)
–
∫
∫
bn-1
+
+
an-1
∫
∫
bn-2
b1
+
+
+
+
an-2
a1
∫
∫
b0
a0
Sistemas

Diagrama de Blocos
 Pela propriedade de comutação
x(t)
1/an
+
bn
+
–
∫
+
an-1
bn-1
∫
+
+
∫
∫
an-2
bn-2
a1
b1
∫
a0
+
∫
b0
+
+
y(t)
Sistemas

Diagrama de Blocos
 Simplificando
x(t)
(forma direta II)
1/an
+
bn
+
–
∫
+
an-1
bn-1
+
∫
+
+
an-2
bn-2
a1
b1
∫
a0
b0
+
+
y(t)