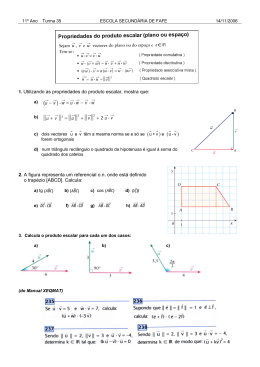
Matemática
A figura (ilustrativa e sem escalas) que segue corresponde à vista superior do trecho de uma praça. Nela se destacam uma região de circulação de pedestres e uma região
sombreada, a ser gramada, composta por três partes e limitada por segmentos de reta
e um setor circular de raio r, conforme indicado.
C
D
E
B
r
A
G
F
região de circulação
Sabe-se que ABEG é um quadrado de lado L m, com L > 7, EF = 13m, DE = 5,2m,
AF = 17m, CD = 3m, CD é paralelo a AF a área do setor circular é igual à metade da área
de ABEG e D, E e F são colineares. Nessas condições, elabore e execute um plano de
resolução de maneira a determinar:
A)
O valor de L (em metros).
B)
A área de toda a região sombreada (em m2).
Resolução
A figura ilustra a vista superior do trecho de uma praça.
Dados:
EF = 13 m; DE = 5,2 m; AF = 17 m; CD = 3 m
Área do setor circular igual a metade da Área do Quadrado ABEG.
A)
O valor de L:
No triângulo retângulo EGF temos:
EG = L ; GF = 17 – L ; EF = 13
Aplicando o Teorema de Pitágoras:
L2 + (17 – L)2 = 132
L2 + 289 – 34L + L2 = 169
2L2 – 34L + 120 = 0
L2 – 17L + 60 = 0
Raízes da equação L = 5 (não convém, pois L > 7) e L = 12 m.
Portanto, o lado do quadrado mede 12 metros.
B)
A área de toda região sombreada
Considerando A1 (área do triângulo EGF); A2 (área do trapézio BCDE) e A3 (área
do setor circular), temos que:
GF ⋅ GE 5 ⋅ 12
=
= 30 m2
2
2
(BE + CD) ⋅ h (12 + 3) ⋅ h
A2 =
=
2
2
A1 =
Se considerarmos o segmento DH a altura do trapézio BCDE temos a semelhança
entre os triângulos DEH e EFG:
DH DE
h 5, 2
=
→
=
→ h = 4, 8 metros
EG EF
12 13
(BE + CD) ⋅ h (12 + 3) ⋅ 4, 8
A2 =
=
= 3 6 m2
2
2
A3: Área do setor circular igual a metade da Área do Quadrado ABEG.
L2
A=
= 72 m2
3
2
Asombreada = A1 + A2 + A3 = 30 + 36 + 72 = 138 m2