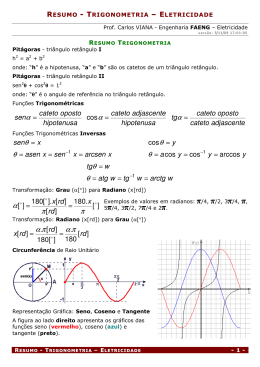
• Matemática – Progressões
pg. 02
• Matemática – Trigonometria no
triângulo
Casas de farinha representam
fonte de renda para o homem sustento familiar e
do interior
pg. 04
• Física – Movimentos de projéteis
pg. 06
• Física – Trabalho e Energia
• Literatura – Realismo e
Naturalismo I
a
rro nergia mecânic
e
F
e
d
strada ormado em e
E
a
d
f
s
r
a vapo é calor tran
a
n
i
u
q
Má a Mamor :
Madeir –
pg. 08
pg. 10
Acervo de
bibliotecas registra
crescimento
de 700%
Ao ingressar na Universidade do Estado do
Amazonas, o aluno tem acesso a um rico
acervo bibliográfico. Em cinco anos, o
número de títulos disponíveis cresceu mais
de 700%. Em 2001, eram 3.661 títulos e
8.235 exemplares. Em 2006, já são 29.058
títulos e 95.180 exemplares.
A esse acervo, soma-se o material didático
disponível em todos os 61 municípios do
interior do Amazonas disponível para os
alunos dos cursos ministrados pela UEA
pelo Sistema Presencial Mediado (Proformar,
Ciência Política e Licenciatura em
Matemática).
A rede de serviços é composta por uma
Biblioteca Central, nove bibliotecas setoriais,
nove bibliotecas de núcleos e 37 minibibliotecas.
A Biblioteca da UEA é informatizada e utiliza
o sistema Pergamun, que permite ao aluno
pesquisar e fazer reservas e renovações de
títulos via Internet. O Pergamun já é utilizado
em cerca de 48 instituições de nível superior
do País, o que possibilita aos alunos da UEA
consulta ao acervo dessas instituições. Todo
esse sistema de informatização utiliza 68
computadores.
Além disso, professores, pesquisadores,
alunos e funcionários da UEA têm acesso à
produção científica mundial atualizada por
meio do Portal de Periódicos da Capes.
Trata-se de uma biblioteca virtual, de fácil
acesso, oferecida pelo governo federal e
mantida pela Capes. O acervo do Portal
compreende mais de 9,5 mil periódicos
completos, 507 revistas científicas e bases
de dados brasileiros de acesso gratuito, 105
bases de dados referenciais e, ainda, seis
bases de dados de patentes com cobertura
internacional e outras fontes de informações
acadêmicas.
O foco da coleção do Portal são as publicações periódicas. Completando essa
coleção, estão incluídos importantes sítios
com textos completos, destacando-se:
Biblioteca Nacional; Escola Paulista de
Medicina; Domínio Público (Ministério da
Educação), entre outros.
Os usuários autorizados para o acesso às
coleções são professores permanentes,
temporários e visitantes, estudantes de
graduação, pós-graduação e extensão,
funcionários permanentes e temporários
vinculados oficialmente às instituições
participantes do Portal.
Com o objetivo de qualificar equipes
técnicas para o usos e a divulgação do
Portal, são desenvolvidos treinamentos em
todas as Unidades Acadêmicas da UEA, por
meio de bibliotecárias capacitadas pela
Capes, bem como treinamento por
representantes das editoras credenciadas.
Matemática
Suponhamos que se queira calcular a soma dos
termos dessa seqüência, isto é, a soma dos 10
termos da PA(2, 4, 6, 8, ..., 18, 20).
Poderíamos obter esta soma manualmente, ou
seja, 2+4+6+8+10+12+14+16+18+20 =110.
Mas se tivéssemos de somar 100, 200, 500 ou
1000 termos? Manualmente seria muito
demorado. Por isso, precisamos de um modo
mais prático para somarmos os termos de uma
PA. Na PA( 2, 4, 6, 8, 10, 12, 14, 16, 18, 20)
observe:
a1+a10 = 2 + 20 = 22
a2+a9 = 4 + 18 = 22
a3+a8 = 6 + 16 = 22
a4+a7 =8 + 14 = 22
a5+a6 = 10 + 12 = 22
Note que a soma dos termos eqüidistantes é
constante (sempre 22) e apareceu exatamente 5
vezes (metade do número de termos da PA,
porque somamos os termos dois a dois). Logo,
devemos, em vez de somarmos termo a termo,
fazermos apenas 5 x 22 = 110, e assim,
determinamos S10 = 110 (soma dos 10 termos).
E agora, se fosse uma progressão de 100 termos,
como a PA(1, 2, 3, 4,...,100), como faríamos?
Procederemos do mesmo modo. A soma do a1
com a100 vale 101 e esta soma vai-se repetir 50
vezes (metade de 100), portanto
S100 = 101x50 = 5050.
Então, para calcular a soma dos n termos de
uma PA, somamos o primeiro com o último
termo e esta soma irá se repetir n/2 vezes.
Assim, podemos escrever:
n
Sn = (a1 + an) ––––
2
Professor CLÍCIO
Progressões
1. Progressão aritmética ( P.A.)
Definição
Consideremos a seqüência ( 2, 4, 6, 8, 10, 12,
14, 16).
Observamos que, a partir do segundo termo, a
diferença entre qualquer termo e seu antecessor
é sempre a mesma:
4 – 2 = 6 – 4 = 10 – 8 = 14 – 12 = 16 – 14 = 2
Seqüências como esta são denominadas progressões aritméticas (PA). A diferença constante é
chamada de razão da progressão e costuma ser
representada por r. Na PA dada temos r = 2.
Podemos, então, dizer que:
Progressão aritmética é a seqüência numérica
onde, a partir do primeiro termo, todos são
obtidos somando uma constante chamada razão.
Notação
Considere a P.A. ( a1, a2, a3, a4, ...., an)
Onde:
a1= primeiro termo
an = último termo, termo geral ou n-ésimo
termo
n = número de termos(se for uma PA finita)
r = razão
Classificação
Quanto à razão:
• (5, 10, 15, 20, 25, 30) é uma PA de razão
r = 5. Toda PA de razão positiva (r > 0) é
crescente.
• (12, 9, 6, 3, 0, -3) é uma PA de razão r = -3.
Toda PA de razão negativa (r < 0) é
decrescente.
• (2, 2, 2, 2, 2,...) é uma PA de razão r = 0.
Toda PA de razão nula (r = 0) é constante ou
estacionária.
Quanto ao número de termos:
• (5, 15, 25, 35, 45, 55) é uma PA de 6 termos e
razão r = 10. Toda PA de n.° de termos finito é
limitada.
• (12, 10, 8, 6, 4, 2,...) é uma PA de infinitos
termos e razão r = -2. Toda PA de n.° de
termos infinito é ilimitada.
Propriedades:
• Numa PA, qualquer termo, a partir do segundo,
é a média aritmética do seu antecessor e do
seu sucessor.
• Numa PA qualquer de número ímpar de
termos, o termo do meio (médio) é a média
aritmética do primeiro termo e do último termo.
Exemplo:
Consideremos a PA(3, 6, 9, 12, 15, 18, 21) e o
termo médio é 12. Observemos que o termo
médio é sempre a média aritmética do primeiro
e do último, ou seja:
3 + 21 = 12
–––––––
2
• A soma de dois termos eqüidistantes dos
extremos de uma PA finita é igual à soma dos
extremos.
Exemplo:
Consideremos a PA (3, 7, 11, 15, 19, 23, 27, 31).
Aplicações
01. (FGV) Verifique se 31/20 é termo da
sucessão.
1+3n
an = ––––––
2n
a) décimo termo; b) quarto termo;
c) sexto termo;
d) oitavo termo;
e) n.d.a.
Solução:
31
1+3n
e an = –––
an = ––––––
20
2n
31
1+3n
––– = –––––
e ⇒ 62n = 20 + 60n
20
2n
2n = 20 ⇒ n = 10 (n ∈ IN)
02. (MACK) Determine o valor de x para que os
números log28, log2(x+9) e log2(x+7)
estejam, nessa ordem, em PA
a) x = 5
b) x = 3
c) x = -3
d) x = -5
e) n.d.a.
Solução:
(log28, log2(x+9) e log2(x+7)) PA
2log2(x+9) = log28 + log2(x+7)
2
2
log2(x+9) =log28(x+7)⇒ x +18x+81= 8x+56
2
x + 10x+25 = 0 ⇒ x = –5
03. (UFAM) Quantos são os números naturais
menores que 98 e divisíveis por 5?
a) 15 números b) 20 números
c) 25 números d) 30 números
e) n.d.a.
Solução:
(0, 5, 10,..................., 95) PA
a1 = 0; an = 95; r = 5
an = a1 + (n–1).r ⇒ 95 = 0 + (n–1).5
95 = (n–1).5 ⇒ 19 = n – 1 ⇒ n = 20
Portanto a quantidade de termos é igual a 20.
04. (UNIP) Numa PA crescente de 6 termos, a
soma dos termos de ordem ímpar é 27, e a
soma dos termos de ordem par é 36.
Escreva essa PA
Solução:
(x–5r, x–3r, x–r, x+r, x+3r, x+5r) P.A.
x–5r + x–r + x+3r=27 ⇒ 3x–3r=27 ⇒ x–r=9
x–3r + x+r + x+5r=36 ⇒ 3x+3r=36 ⇒ x+r=12
Termo Geral
Uma PA de razão r pode ser escrita assim:
PA(a1, a2, a3, a4, ...., an–1 an)
Portanto, o termo geral será:
an = a1 + (n – 1)r, para n ∈ N*
Soma dos Termos de uma PA finita
Consideremos a seqüência (2, 4, 6, 8, 10, 12,
14, 16, 18, 20). Trata-se de uma PA de razão 2.
Logo a PA é dada por: (3, 6, 9, 12, 15, 18) P.A.
05. (UEA) O perímetro de um triângulo retângulo
mede 24cm. Calcule as medidas dos lados,
sabendo-se que elas estão em P.A.
2
a) 5cm, 9cm e 10cm b) 4cm, 6cm e 10cm
c) 4cm, 5cm e 15cm d) 5cm, 6cm e 13cm
e) n.d.a.
Solução:
(x–r, x, x+r)P.A.
x–r + x + x+r = 24 ⇒ 3x = 24 ⇒ x = 8
8–r, 8, 8+r representam os lados de um triângulo
retângulo.
2
2
2
(8–r) + 8 = (8+r)
2
2
64 –16r + r + 64 = 64 + 16r + r
32r = 64 ⇒ r = 2
Logo os lados são 6cm, 8cm e 10cm.
06. (FGV) Ache a progressão aritmética em que
S10 = –65 e S20 = 170.
a) (-20, -17, -14,..........)
b) (-20, -15, -10,..........)
c) (-10, -17, -24,..........)
d) (-20, -17, -14,..........)
e) n.d.a
Solução:
(a1 + a10).10
= –65 ⇒ a1+a10=–13
S10=–65 ⇒ ––––––––––––
2
(a1 + a20).10
S20=170 ⇒ –––––––––––– = 170 ⇒ a1+a20=17
2
Logo a P.A. é dada por (-20, -17, -14,..........)
2. Progressão geométrica( PG)
Definição
Entenderemos por progressão geométrica – PG
– como qualquer seqüência de números reais
ou complexos, onde cada termo, a partir do
segundo, é igual ao anterior, multiplicado por
uma constante denominada razão.
Exemplos:
(1, 2, 4, 8, 16, 32, ... ) PG de razão 2
(5, 5, 5, 5, 5, 5, 5, ... ) PG de razão 1
(100, 50, 25, ... ) PG de razão 1/2
(2, –6, 18, –54, 162, ...) PG de razão –3
Fórmula do termo geral
Seja a PG genérica: (a1, a2, a3, a4, ... , an, ... ) ,
onde a1 é o primeiro termo, e an é o n-ésimo
termo, ou seja, o termo de ordem n. Sendo q a
razão da PG, da definição podemos escrever:
a2= a1 . q
2
a3= a2 . q = (a1 . q).q = a1 . q
2
3
a4= a3 . q = (a1 . q ).q = a1 . q
................................................
................................................
n-1
Infere-se (deduz-se) que: an = a1 . q , que é
denominada fórmula do termo geral da PG.
Genericamente, poderemos escrever:
j-k
aj = a k . q
Exemplos:
a) Dada a PG (2,4,8,... ), pede-se calcular o
décimo termo.
Temos: a1 = 2, q = 4/2 = 8/4 = ... = 2. Para
calcular o décimo termo, ou seja, a10, vem
pela fórmula:
9
9
a10 = a1 . q = 2 . 2 = 2. 512 = 1024
b)Sabe-se que o quarto termo de uma PG
crescente é igual a 20, e o oitavo termo é
igual a 320. Qual a razão desta PG?
Temos a4 = 20 e a8 = 320. Logo, podemos
8–4
escrever: a8 = a4 . q . Daí, vem:
4
320 = 20.q
4
Então q =16 e portanto q = 2.
Nota: Uma PG genérica de 3 termos, pode ser
expressa como:
(x/q, x, xq), onde q é a razão da PG.
Propriedades principais
• Em toda PG, um termo é a média geométrica
dos termos imediatamente anterior e posterior.
Exemplo:
PG (A, B, C, D, E, F, G)
2
2
Temos então: B = A . C ; C = B . D ;
2
2
D = C . E ; E = D . F, etc.
• O produto dos termos eqüidistantes dos
extremos de uma PG é constante.
Exemplo:
PG (A, B, C, D, E, F, G)
2
Temos então: A . G = B . F = C . E = D . D = D
Soma dos n primeiros termos de uma PG
Seja a PG (a1, a2, a3, a4, ... , an , ...). Para o
cálculo da soma dos n primeiros termos Sn ,
vamos considerar o que segue:
Sn = a1 + a2 + a3 + a4 + ... + an-1 + an
Multiplicando ambos os membros pela razão q,
vem:
Sn . q = a1 . q + a2 .q + .... + an-1 . q + an .q .
Logo, conforme a definição de PG, podemos
reescrever a expressão acima como:
Sn . q = a2 + a3 + ... + an + an . q
Observe que a2 + a3 + ... + an é igual a Sn – a1.
Logo, substituindo, vem:
Sn . q = Sn – a1 + an . q
Daí, simplificando convenientemente,
chegaremos à seguinte fórmula da soma:
an . q – a1
Sn = ––––––––––
q–1
n-1
Se substituirmos an = a1 . q , obteremos uma
nova apresentação para a fórmula da soma, ou
seja:
qn – a1
Sn = a1 –––––––
q–1
Soma dos termos de uma PG decrescente e
ilimitada
Considere uma PG ILIMITADA ( infinitos termos)
e decrescente. Nestas condições, podemos
considerar que no limite teremos an = 0.
Substituindo na fórmula anterior, encontraremos:
a1
S∞ = ––––––
q–1
Aplicações
01. (UFMG) Dados os números 1, 3 e 4, nesta
ordem, determine o número que se deve
somar a cada um deles para que se tenha
uma progressão geométrica.
a) –5
d) –8
b) –6
e) n.d.a.
c) –7
Solução:
(x+1, x+3, x+4) P.G.
2
(x+3) = (x+1).(x+4)
2
2
x + 6x + 9 = x + 5x + 4 ⇒ x = –5
02. (UEA) Numa P.G., o primeiro termo é 4 e o
quarto termo é 4000. Qual é a razão dessa
P.G.
a) 10
d) 40
b) 20
e) n.d.a.
c) 30
Solução:
a1 = 4 e a4 = 4000
3
3
a4 = a1.q ⇒ 4000 = 4. q
3
q = 1000 ⇒ q = 10
03. (UFPA) Numa progressão geométrica, a
diferença entre o 2.° e o 1.° termo é 9 e a
diferença entre o 5.° e o 4.° termo é 576.
Calcule o primeiro termo dessa progressão.
a) 3
d) 6
b) 4
e) n.d.a.
c) 5
Solução:
Desafio
Matemático
01. Se numa seqüência temos que f(1) =
3 e f (n + 1) = 2.f(n) + 1, então o valor
de f(4) é:
a) 4
d) 31
b) 7
e) 42
02. O trigésimo primeiro termo de uma P.
A. de 1.° termo igual a 2 e razão 3 é:
a) 63
d) 95
b) 65
e) 102
a) a = –2
b) a = 2
c) a = –3
d) a = 3
e) n.d.a.
Solução:
(a,................, 486) P.G.
q=3
5
5
a6 = a1.q ⇒ 486 = a. 3 ⇒ a = 2
05. (FGV) Resolva a equação:
10x + 20x + 40x + .............+ 1280x =
7650, sabendo que os termos do 1.°
membro estão em P.G.
a) x = -3
b) x = 3
c) x = 4
d) x = -4
e) n.d.a.
Solução:
(10x, 20x, ................, 1280x) P.G.
n–1
1280x = 10x.2
128 = 2n-1 ⇒ n = 8
10x + 20x + 40x + .............+ 1280x = 7650
10x.(28 – 1)
––––––––––– = 7650 ⇒ x = 3
2–1
3
c) 92
03. O primeiro termo de uma progressão
aritmética, com a7 = 12 e razão igual a
5 é:
a) –18
d) –42
b) 18
e) 2
c) 42
04. Três números positivos estão em
progressão aritmética. A soma deles é
12 e o produto 18. O termo do meio é:
a) 2
d) 4
b) 6
e) 3
c) 5
05. A soma dos múltiplos de 3
compreendidos entre 100 e 200 é:
a) 5000
d) 4950
b) 3950
e) 4500
c) 4000
06. Um cinema possui 20 poltronas na
primeira fila, 24 poltronas na Segunda
fila, 28 na terceira fila, 32 na quarta fila
e as demais fileiras se compõem na
mesma seqüência. Quantas filas são
necessárias para a casa ter 800
lugares?
a) 13
d) 16
b) 14
e) 17
c) 15
07. Se a razão de uma P.G. é maior que 1
e o primeiro termo é negativo, a P.G. é
chamada:
a) decrescente
c) constante
e) singular
04. (UFAM) Inserindo- se quatro meios
geométricos entre a e 486, obtém-se uma
P.G. de razão igual a 3. Qual o valor de a?
c) 15
b) crescente
d) alternante
08. Em uma progressão geométrica, o
quinto termo é 24 e o oitavo termo é 3.
A razão entre o sexto termo e o
décimo é:
a) 4
d) 16
b) 8
e) 1/16
c) 1/8
09. Sabendo que a sucessão
(x – 2, x + 2, 3x – 2,...) é uma P.G.
crescente, então o quarto termo é :
a) 27
d) 16
b) 64
e) 54
c) 32
10. Dada a progressão geométrica
1, 3, 9, 27,..., se a sua soma é 3280,
então ela apresenta:
a) 9 termos
d) 6 termos
b) 8 termos c) 7 termos
e) 5 termos
Desafio
Matemático
01. Considere o triângulo retângulo
representado na figura abaixo, onde
AB = 3 e AC = 4.
Matemática
Professor CLÍCIO
Nomenclatura dos catetos
Os catetos recebem nomes especiais de acordo
com a sua posição em relação ao ângulo sob
análise. Se estivermos operando com o ângulo
C, então o lado oposto, indicado por c, é o
cateto oposto ao ângulo C e o lado adjacente ao
ângulo C, indicado por b, é o cateto adjacente
ao ângulo C.
Trigonometria no triângulo
1. Trigonometria:
Trigonometria do Triângulo Retângulo
A trigonometria possui uma infinidade de
aplicações práticas. Desde a antiguidade, já se
usava da trigonometria para obter distâncias
impossíveis de serem calculadas por métodos
comuns.
Algumas aplicações da trigonometria são:
Determinação da altura de um certo prédio.
Um dos objetivos da trigonometria é mostrar a
utilidade do conceitos matemáticos no nosso
cotidiano. Iniciaremos estudando as propriedades geométricas e trigonométricas no triângulo
retângulo. O estudo da trigonometria é extenso
e minucioso.
C é:
O valor de cos ^
a) 4/5
d) 5/4
b) 3/5
e) 3/4
Propriedades do triângulo retângulo
c) 5/3
02. Se um cateto e a hipotenusa de um
triângulo medem a e 3a, respectivamente, então o cosseno do ângulo
oposto ao menor lado é:
a)
b)
d)
e)
c)
03. Duas rodovias A e B encontram-se em
O, formando um ângulo de 30°. Na
rodovia A existe um posto de gasolina
que dista 5km de O. O posto dista da
rodovia B:
a) 5Km
d) 15Km
b) 10Km
e) 1,25Km
c) 2,5Km
b) 3/5
e) 4
c) 4/5
05. Sendo sen a + cos a = m, então
sen a . cos a é igual a:
m–1
a) –––––
2
m+1
d) –––––
2
2
m –1
b) ––––––
2
m
e) ––––
2
2
m +1
c) ––––––
2
06. Sabendo-se que cos x = 1/4 e que x é
um arco do 4.° quadrante, pode-se
afirmar que o valor real positivo de
y= [sec2x – secx . cos secx].[1 –
cotgx]–1é:
a) 132
d) 1253
b) 16
e) 43
Os gregos determinaram a medida do raio da
Terra, por um processo muito simples.
Seria impossível se medir a distância da Terra à
Lua, porém com a trigonometria isso torna
simples.
Um engenheiro precisa saber a largura de um rio
para construir uma ponte, o trabalho dele é mais
fácil quando ele usa dos recursos trigonométricos.
Um cartógrafo (desenhista de mapas) precisa
saber a altura de uma montanha, o comprimento
de um rio, etc. Sem a trigonometria ele demoraria
anos para desenhar um mapa.
Tudo isto é possível calcular com o uso da
trigonometria do triângulo retângulo.
Funções trigonométricas básicas
As Funções trigonométricas básicas são
relações entre as medidas dos lados do
triângulo retângulo e seus ângulos. As três
funções básicas mais importantes da
trigonometria são: seno, cosseno e tangente. O
ângulo é indicado pela letra x.
Triângulo Retângulo
04. Um retângulo com lados adjacentes
medindo sen α e cos α, com 0<α<π/2,
tem perímetro igual a
. A área desse
retângulo é:
a) 1/4
d) 5/4
Ângulos: Um triângulo retângulo possui um
ângulo reto e dois ângulos agudos complementares.
Lados: Um triângulo retângulo é formado por
três lados, uma hipotenusa (lado maior) e outros
dois lados que são os catetos.
Altura: A altura de um triângulo é um segmento
que tem uma extremidade num vértice e a outra
extremidade no lado oposto ao vértice, sendo
que este segmento é perpendicular ao lado
oposto ao vértice. Existem 3 alturas no triângulo
retângulo, sendo que duas delas são os catetos.
A outra altura (ver gráfico acima) é obtida
tomando a base como a hipotenusa, a altura
relativa a este lado será o segmento AD,
denotado por h e perpendicular à base.
É um triângulo que possui um ângulo reto, isto
é, um dos seus ângulos mede noventa graus,
daí o nome triângulo retângulo. Como a soma
das medidas dos ângulos internos de um
triângulo é igual a 180°, então os outros dois
ângulos medirão 90°.
Observação: Se a soma de dois ângulos mede
90°, estes ângulos são denominados
complementares, portanto podemos dizer que o
triângulo retângulo possui dois ângulos
complementares.
Tomando um triângulo retângulo ABC, com
hipotenusa H medindo 1 unidade, então o seno
do ângulo sob análise é o seu cateto oposto CO
e o cosseno do mesmo é o seu cateto adjacente
CA. Portanto a tangente do ângulo analisado
será a razão entre seno e cosseno desse ângulo.
Lados de um triângulo retângulo
Os lados de um triângulo retângulo recebem
nomes especiais. Estes nomes são dados de
acordo com a posição em relação ao ângulo
reto. O lado oposto ao ângulo reto é a
hipotenusa. Os lados que formam o ângulo reto
(adjacentes a ele) são os catetos.
2. Relações Trigonométricas
Relação fundamental
Para todo ângulo x (medido em radianos), vale
a importante relação: cos²(x) + sen²(x) = 1
Fórmulas derivadas das fundamentais
c) 49
Já sabemos as cinco fórmulas fundamentais da
Trigonometria, a saber:
07. Se um ângulo é igual ao seu complemento, então o seno deste ângulo é
igual a:
a)
b)
d) 1
e)
b) 2
e) 5
Fórmula I – Relação Fundamental da
Trigonometria.
2
2
sen x + cos x = 1
2
2
[o mesmo que (senx) + (cosx) = 1]
Fórmula II – Tangente.
senx
1
tgx = ––––– = –––––– , com cosx ≠ 0
cosx
cotgx
Fórmula III – Co-tangente.
cosx
1
cotgx = ––––– = ––––, com senx ≠ 0
senx
tgx
Fórmula IV – Secante.
1
secx = ––––––, com cosx ≠ 0
cosx
c)
08. O valor de k que verifica simultaneamente sec x = k/2 e tgx=
é:
a) 1
d) 4
Dado um arco trigonométrico x, temos:
Para padronizar o estudo da Trigonometria,
adotaremos as seguintes notações:
c) 3
4
AH = diâmetro da circunferência = 2R
(R = raio)
AO = OH = raio da circunferência = R
Medidas dos lados do triângulo ABC:
AB = c, BC = a e AC = b.
Para deduzir o teorema dos senos, vamos iniciar
observando que os ângulos H e B são
congruentes, ou seja, possuem a mesma
medida, pois ambos estão inscritos no mesmo
arco CA. Além disso, podemos afirmar que o
ângulo ACH é reto (90°), pois AH é um diâmetro.
Portanto o triângulo ACH é um triângulo
retângulo.
Podemos então escrever:
sen H = sen B = cateto oposto/hipotenusa =
AC / AH = b/2R.
Logo, fica: senB = b/2R e, portanto, b/senB=2R.
Analogamente, chegaríamos às igualdades
c/senC = 2R e a/senA = 2R
Como essas três expressões são todas iguais a
2R, poderemos escrever finalmente:
A
B
C
–––––– = –––––– = ––––– = 2R
senA
senB
senC
Essa expressão mostra que as medidas dos
lados de um triângulo qualquer são
proporcionais aos senos dos ângulos opostos a
esses lados, sendo a constante de
proporcionalidade igual a 2R, onde R é o raio da
circunferência circunscrita ao triângulo ABC.
Fórmula V – Co-secante.
1
cosecx = ––––––, com senx ≠ 0
senx
Nota – Considere, nas fórmulas acima, a
impossibilidade absoluta da divisão por ZERO.
Assim, por exemplo, se cosx = 0, não existe a
secante de x; se sen x = 0, não existe a cosec x.
Para deduzir duas outras fórmulas muito
importantes da Trigonometria, vamos partir da
fórmula I acima, inicialmente dividindo ambos
2
os membros por cos x ≠ 0. Teremos:
2
2
sen x
cos x
1
–––––––
+ ––––––
= ––––––
2
2
2
cos x
cos x
cos x
Das fórmulas anteriores, concluiremos inevitavelmente a seguinte fórmula que relaciona a tangente e a secante de um arco trigonométrico x:
2
2
tg x + 1 = sec x
2
Se em vez de dividirmos por cos x, dividíssemos
2
ambos os membros por sen x, chegaríamos a:
2
2
cotg x + 1 = cosec x
As duas fórmulas anteriores são muito
importantes para a solução de exercícios que
comparecem nos vestibulares; merecem, por
isto, uma memorização. Aliás, as sete fórmulas
anteriores têm necessariamente de ser
memorizadas, e isso é apenas o início! A
Trigonometria, infelizmente, depende de
memorizações de fórmulas, mas, se você
souber deduzi-las, como estamos tentando
mostrar aqui, as coisas ficarão muito mais
fáceis! Portanto fique tranqüilo(a).
5. Lei dos Co-senos
Considere o triângulo ABC na figura abaixo:
Desafio
Matemático
01. Sendo O o centro da circunferência de
raio unitário, então x = BC vale:
a) 1
d) 0,5
(UEA) Sendo sena + cosa = m, então sena.cosa
é igual a:
c) 0,6
02. O valor de k, para o qual
(cosx + senx)2 + k .senx. cos x – 1=0
é uma identidade , é:
a) –1
d) 1
Arapuca
b) 0,8
e) 0,4
b) –2
e) 2
c) 0
03. Simplificando a expressão
a) (m-1)/2
b) (m + 1)/2
c) m/2
d) (2m-1)/2 e) n.d.a.
Solução:
sena + cosa = m
2
2
(sena + cosa) = m
2
2
2
sen a + 2sena.cos.a + cos a = m
2
2
(sen2a + cos a) + 2sena.cos.a = m
2
1 + 2sena.cos.a = m
2
sena.cosa = (m – 1)/2
AH = altura do triângulo em relação à base CB.
Medidas dos lados: AC = b, AB = c e CB = a.
Podemos escrever no triângulo AHB:
2
2
2
AH + HB = c (Teorema de Pitágoras).
Analogamente, podemos aplicar o teorema de
2
2
2
Pitágoras no triângulo AHC: b = CH + AH
Mas CH = CB – HB = a – HB
2
2
2
Portanto: b = (a - HB) + AH
2
2
2
2
b = a – 2.a.HB + HB + AH
2
2
2
2
Observe que HB + AH = AB = c
2
2
2
Então fica: b = a + c – 2.a.HB
No triângulo retângulo AHB, podemos escrever:
cosB = cateto adjacente/hipotenusa = HB/c
Daí, HB = c.cosB
Substituindo, fica:
2
2
2
b = a + c – 2.a.c. cosB
Da fórmula acima, concluímos que num
triângulo qualquer, o quadrado da medida de
um lado é igual à soma dos quadrados das
medidas dos outros dois lados, menos o dobro
do produto das medidas desses lados pelo coseno do ângulo que eles formam.
Analogamente, poderemos escrever:
2
2
2
a = b + c – 2.b.c.cosA
2
2
2
c = a + b – 2.a.b.cosC
Em resumo:
2
2
2
a = b + c – 2.b.c.cosA
2
2
2
b = a + c – 2.a.c.cosB
2
2
2
c = a + b – 2.a.b.cosC
(FGV) Simplificar a expressão:
senx
cosx
–––––––––– + –––––––– .
1 + cotgx
1 + tgx
1
a) ––––––––––––
senx + cosx
1
b) ––––––––––––
senx – cosx
1
c) ––––––
senx
1
c) ––––––
cosx
e) n.d.a.
Solução:
, encontramos:
a)
b)
c)
d)
E = 1 + senx
1
2
2
E = sen x – cos x
E = 1 – senx
cosx
e) E = –––––––––
1+senx
04. Na figura abaixo, determinar o valor de
AB.
a) 65
d) 25
b) 45
e) 67
c) 75
05. Na figura abaixo, tem-se representado
o losango ABCD, cuja diagonal menor
mede 4 cm.
4. Lei dos Senos
Considere a figura abaixo, em que se vê um
triângulo ABC inscrito numa circunferência de raio
R. Observe que também podemos dizer que a
circunferência está circunscrita ao triângulo ABC.
Caiu no vestibular
(UEA) Num triângulo dois lados de
medidas 4cm e 8cm formam entre si
um angulo de 60°. Qual a medida do
outro lado?
a)
b)
d)
e) n.d.a.
c)
Solução:
Ora, sendo x a medida do terceiro lado, teremos:
2
2
2
x = 4 + 8 – 2.4.cos60° = 16 + 64 – 8.(1/2), já
que cos60° = 1/2.
2
x = 16 + 64 – 4 = 76
x=
cm
Na figura acima, temos:
5
A medida do lado desse losango, em
cm, é:
a)
b) 6
d) 4
e)
c)
Desafio
Físico
Física
Professor CARLOS Jennings
Movimentos de projéteis
01. (UFSC) Duas bolinhas, A e B, partem
ao mesmo tempo de uma certa altura H
acima do solo, sendo que A em queda
livre e B com velocidade vo na direção
horizontal. Podemos afirmar que:
a) A chega primeiro ao solo.
b) B chega primeiro ao solo.
c) A ou B chega primeiro, dependendo da
altura.
d) A ou B chega primeiro, dependendo da
velocidade inicial vo de B.
e) As duas chegam juntas.
02. (UFPR) Uma bola rola sobre uma mesa
horizontal de 1,225m de altura e vai
cair num ponto situado à distância de
2,5m, medida horizontalmente a partir
da beirada da mesa. Qual a velocidade
da bola, em m/s, no instante em que
ela abandonou a mesa? (g = 9,8m/s2).
a) 5m/s
c) 15m/s
b) 10m/s
d) 20m/s
b) 10,5m/s
e) 6,6m/s
c) 8m/s
04. Um jogador chuta uma bola com uma
velocidade inicial de 20m/s, sob um
ângulo de 60° com a horizontal. Calcule
a altura máxima que a bola irá atingir.
a) 5m
c) 15m
b) 10m
d) 20m
e) 25m
05. (Fuvest-SP) Um gato, de um quilograma,
dá um pulo, atingindo uma altura de
1,25m e caindo a uma distância de 1,5m
do local do pulo (g = 10m/s2). A
componente vertical da velocidade inicial
e a velocidade horizontal do gato valem,
respectivamente.
a) 5m/s e 1,5m/s
c) 5m/s e 15m/s
e) 5,5m/s e 1m/s
b) 1,5m/s e 5m/s
d) 0,5m/s e 1,5m/s
06. Uma bola rola sobre uma mesa de
80cm de altura, com velocidade constante de 5m/s. Ao abandonar a mesa
(g = 10m/s2), a bola cai, tocando o
solo no ponto situado, em relação à
mesa:
a) 3m
d) 0,5m
b) 2m
e) 1,5m
c)1m
07. Uma pedra de 4kg é lançada
verticalmente de baixo para cima, com
uma velocidade inicial de 80m/s. qual a
altura máxima alcançada pela pedra?
a) 320m
d) 20m
Corpos que se movimentam nas imediações da
superfície terrestre, sem contato com o solo e
sujeitos apenas à atração gravitacional (força
peso), estão submetidos à mesma aceleração: a
da gravidade (g).
2. LANÇAMENTO VERTICAL
Equações: origem no ponto de lançamento (S0 =
0); trajetória orientada no sentido do movimento.
1. QUEDA LIVRE (MUV acelerado em trajetória
vertical).
Equações: origem no ponto inicial (S0 = 0);
velocidade inicial nula (v0 = 0); resistência do ar
nula.
Caiu no vestibular
(UEA) Se uma pedra é lançada verticalmente
para cima, a partir do solo, com velocidade
inicial vo = 30m/s, ela atingirá uma altura
máxima h, antes de voltar ao solo. Desprezando
o atrito com o ar e fazendo g = 10m/s2, o valor
de h será:
As proporções de Galileu
A área de cada triângulo da figura abaixo é
numericamente igual ao deslocamento d.
a) 45m
b) 35m
c) 20m
d) 10m
e) 5m
Solução:
Na altura máxima, o móvel pára (v = 0). Então:
v = vo + gt ∴ 0 = 30 + 10 . t ∴ t = 3s
A altura máxima atingida:
2
2
10.3
gt
S= vo.t – ––– ∴ S= 30.3 – –––––– ∴ S=45m
2
2
e) 25m/s
03. Um corpo de 2kg deve ser lançado
horizontalmente do alto de uma rampa
de altura 45m, devendo atingir um
buraco a 20m do pé da rampa. Qual
deve ser o valor da velocidade de
lançamento?
a) 12m/s
d) 7,6m/s
o móvel percorre em 1s, 2s, 3s e 4s,
respectivamente: d, 3d, 5d e 7d. Então:
x = d + 3d = 4d
y = 5d + 7d = 12d
x
A razão ––– vale:
y
x
4d
1
––– = –––– = ––––
y
12d
3
b) 220m
c) 120m
e) Nenhuma é correta.
Conclusão:
Em tempos iguais e consecutivos, um móvel em
queda livre percorre distâncias cada vez maiores,
na proporção dos ímpares consecutivos: no
primeiro segundo, o móvel cai uma distância d;
no segundo seguinte, percorre 3d; no terceiro
segundo, 5d, e assim por diante.
Arapuca
Um objeto de 2kg é lançado verticalmente para
baixo, com velocidade inicial de 20m/s. Atinge o
solo 4s após o lançamento. De que altura o
corpo foi lançado? Com que velocidade ele
atinge o solo?
Solução:
A altura do lançamento:
2
10.16
gt
S= vo.t – ––– ∴ S= 20.4 – –––––– ∴ S=160m
2
2
A velocidade ao chegar ao solo:
v = vo + gt ∴ 20 + 10 . 4 ∴ v = 60m/s
Importante: observe que a massa do corpo
(2kg) não interferiu na resposta.
Caiu no vestibular
(UEA) A expressão popular que afirma que o
gato tem “sete vidas” justifica-se pelo fato de
eles conseguirem se sair bem de algumas
situações difíceis. No caso de uma queda, por
exemplo, eles podem atingir o chão, sem se
machucar, se a velocidade final for cerca de
8m/s. De que altura máxima eles podem cair,
sem o perigo de perder uma de suas “vidas”?
a) 2,0m
b) 2,5m
c) 3,2m
d) 4,0m
e) 4,5m
Solução:
Procuremos o tempo:
v = vo + gt ∴ 8 = 0 + 10t ∴ t = 0,8s
Consideremos g = 10m/s2 e calculemos a altura:
2
2
gt
10.(0,8)
S= –––– ∴ S= –––––––– ∴ S=3,2m
2
2
3. LANÇAMENTO HORIZONTAL
A partir de um ponto situado a uma altura h,
acima do solo, o móvel é lançado
horizontalmente e percorre uma trajetória
parabólica, que pode ser construída utilizandose a composição de dois movimentos
independentes:
a) Movimento horizontal – Nesse movimento, o
corpo percorre espaços iguais (designados
por L, na Figura 2) em tempos iguais:
movimento uniforme (velocidade constante).
b) Movimento vertical – Nessa direção, o móvel
está em queda livre (MUV acelerado) a partir
do repouso. Os deslocamentos verticais
obedecem às Proporções de Galileu: 1d, 3d,
5d, ..., (2n – 1)d.
Arapuca
(UEA) Um corpo é abandonado em queda livre
de uma determinada altura. Observa-se que, nos
dois primeiros segundos de seu movimento, ele
cai x metros. Já nos dois segundos seguintes, o
corpo desloca-se y metros. A razão x/y vale,
portanto:
a) 1
b) 1/2
c) 1/3
d) 2
e) 3
Solução:
O intervalo é de 4s. Pelas proporções de Galileu,
6
Importante: o alcance é o mesmo para
diferentes corpos, lançados com a mesma
velocidade inicial e com ângulos de lançamento
complementares (aqueles cuja soma vale 90°).
Arapuca
Importante: para corpos lançados da mesma
altura, o tempo de queda é o mesmo,
independente das massas dos corpos e de suas
velocidades horizontais de lançamento
(desprezando-se os efeitos do ar).
Um objeto é lançado obliquamente com uma
velocidade inicial de 100m/s, que forma com a
horizontal um ângulo de 60°. Calcule a altura
máxima atingida pelo móvel e a distância do
ponto de lançamento ao ponto em que o móvel
toca o solo.
Aplicação
Solução:
As componentes da velocidade valem:
vox=vo . cos θ =100 . cos 60°=100.0,5 =50 m/s
voy = vo . sen θ = 100 . sen 60°= 100 . 0,866 =
86,6m/s
Calculemos o tempo de subida, usando a
expressão da velocidade vertical. No ponto mais
alto, vy = 0:
2
gt
vy = voy – –––– ∴ 0 = 86,6 – 10t ∴ t= 8,66s
2
A altura atingida pelo móvel (MUV retardado):
2
gt
10 . (8,66)2
h = voy – ––– = 86,6 . 8,66 – ––––––––– = 375m
2
2
Calculemos o alcance (distância horizontal
percorrida em MU). O tempo é o de subida mais
o de descida (8,66s + 8,66s):
Uma bolinha rola por toda a extensão de uma
mesa horizontal de 5m de altura e a abandona
com uma velocidade horizontal de 12m/s. Calcule
o tempo de queda e a distância do pé da mesa
ao ponto onde cairá a bolinha (g = 10m/s2).
Solução:
Calculemos, inicialmente, o tempo de queda,
considerando apenas o movimento vertical
(queda livre – MUV acelerado):
2
gt
10 2
2
H = ––– ∴ 5= ––– t ∴ 5= 5t ∴ t=1s
2
2
Considerando agora o movimento horizontal
(uniforme), teremos:
SH
vH = –––
∴ SH = vH.t = 12 . 1 =12m
t
(o corpo cairá a 12m do pé da mesa).
Sh = vox . t = 50 . 17,32 = 866m
4. LANÇAMENTO OBLÍQUO
A velocidade de lançamento forma com a
horizontal um ângulo distinto de 0° e de 90°.
Exercícios
01. (PUC-RJ) Uma pedra é lançada
verticalmente para cima. No ponto
mais alto da trajetória, pode-se dizer
que a sua velocidade v e a sua
aceleração a têm os seguintes valores,
em módulo:
a) v = 0 e a = 0
c) v = a
e) v = 0 e a = g/2
A velocidade Vo pode ser decomposta em duas
componentes: Vox (componente da velocidade
no eixo dos x) e Voy (componente da velocidade
no eixo dos y):
Vox = vo . cos θ
Voy = vo . sen θ
O lançamento oblíquo resulta da composição de
dois movimentos independentes:
a) Movimento horizontal – Esse movimento é
uniforme, uma vez que Vox é constante
(desprezando-se a resistência do ar).
b) Movimento vertical – Nesse movimento, a
velocidade é variável, pois o corpo está
sujeito à aceleração da gravidade: na subida,
o movimento é retardado (velocidade e
aceleração têm sentidos contrários); na
descida, o movimento é acelerado
(velocidade e aceleração têm sentidos iguais).
b) v = g e a = 0
d) v = 0 e a = g
02. De um ponto a 20m do solo, lança-se,
verticalmente para cima, um objeto
com velocidade inicial de 10m/s.
Despreze a resistência do ar e
considere g = 10m/s2. Considere as
afirmativas:
I. A altura máxima atingida é de 25m, em
relação ao solo.
II. O objeto atinge o solo com velocidade
de 10m/s, em módulo.
III. O tempo, do lançamento até o retorno
ao solo, é de 2s.
São corretas:
a) Apenas a I. b) Apenas a II.
c) Apenas a III. d) I e II.
e) II e III.
03. (Udesc-SC) Um jogador de basquete
arremessa uma bola verticalmente
para cima, com velocidade inicial de
15m/s. Sabendo-se que a bola subiu
durante 1,5s, calcule, em metros, a
altura máxima que ela atingiu a partir
do seu ponto de lançamento,
desprezando a resistência do ar.
a) 10,5m
d) 13m
7
b) 11,25m
e) 14,4m
c) 12,5m
Desafio
Físico
01. (PUC–SP) Você atira um corpo de
200g verticalmente para cima, a partir
do solo, e ele atinge uma altura de 3m
antes de começar a cair. Considerando
a aceleração da gravidade 9,8m/s2 e
nula a resistência do ar, a velocidade
de lançamento foi de:
a) 7,67m/s
d) 7m/s
b) 8,76m/s
e) 6m/s
c) 6,76m/s
02. Um pára-quedista, quando a 120m do
solo, deixa cair uma bomba, que leva
4s para atingir o solo. Qual a velocidade de descida do pára-quesdista?
a) 1m/s
d) 8m/s
b) 2m/s
e) 10m/s
c) 5m/s
03. Um buriti cai do alto de um buritizeiro
e, entre 1s e 2s, percorre 4,5m. As
distâncias percorridas durante o
terceiro e o quarto segundos de
queda são, respectivamente:
a) 5,5m e 6,5m
c) 7,5 e 10m
e) 7,5m e 10,5m
b) 6,5m e 7,5m
d) 7m e 10,5m
04. Um corpo em queda livre sujeita-se à
aceleração gravitacional de 10m/s2.
Ele passa por um ponto A com
velocidade de 10m/s e por um ponto
B com velocidade de 50m/s. A
distância entre os pontos A e B é de:
a) 100m
d) 160m
b) 120m
e) 240m
c) 140m
05. (FESP–PE) Do alto de um edifício,
abandona-se uma bola de ferro que
durante o último segundo percorre
25m. A altura do edifício vale, em
metros:
a) 45
c) 35
b) 40
d) 80
e) 125
06. Um ouriço de castanha desprendeu-se
do alto de uma castanheira de 20m. O
tempo de queda e a velocidade do
ouriço ao chegar ao solo são,
respectivamente:
a) 2s e 20m/s
c) 3s e 30m/s
e) 5s e 50m/s
b) 20s e 2m/s
d) 4s e 40m/s
07. Do alto de uma torre, um garoto deixa
cair uma pedra, que demora 2s para
chegar ao solo. Qual a altura dessa
torre?
a) 10m
c) 30m
b) 20m
d) 40m
e) 50m
08. Uma pedra é arremessada
verticalmente para cima, com
velocidade inicial de 30m/s. Calcule a
altura máxima que ela atinge?
a) 15m
c) 35m
b) 25m
d) 45m
e) 55m
Anota
Aí!
O Sol ocupa uma posição central no
mosaico energético da Terra. A energia
dele emanada induz a formação de todas
as outras formas de energia, exceto a
nuclear.
A energia solar dá causa aos movimentos
dos ventos e das águas, que são formas
de energia mecânica. Essa energia
alimenta as usinas e os moinhos para a
geração de energia elétrica que chega às
nossas casas, a qual, por seu turno, é
transformada em energia térmica (no
chuveiro), em energia mecânica (no
movimento do liquidificador), em energia
luminosa (nas lâmpadas), etc. É pela
energia de radiação provinda do Sol que
se formam os ventos e se aquecem os
rios, realizando-se, assim, o ciclo da
água, que vai propulsionar usinas as
hidroelétricas.
Como se não bastassem todas as formas
de energia que derivam do Sol, a energia
de radiação ainda pode ser usada
diretamente para produzir energia
elétrica, por meio das células
fotoelétricas, e também como energia
termoelétrica, por meio do calor.
Utilizar energia solar como fonte de
energia elétrica pode resolver muitos
problemas da vida moderna, em que,
indiscriminadamente, fabricam-se
equipamentos e máquinas movidos a
eletricidade.
A utilização de células fotoelétricas para a
produção de energia elétrica também
pode representar uma alternativa em
regiões de difícil acesso como a
Amazônia, onde o fornecimento de
energia solar é abundante o ano inteiro.
Física
→
c) Trabalho de Fat (θ = 180°):
τ Fat = Fat.d.cos180° = 10.10.(−1) = −100J
(trabalho resistente).
Energia Mecânica – Chamamos de Energia
Mecânica a todas as formas de energia
relacionadas com o movimento de corpos ou
com a capacidade de colocá-los em movimento
ou deformá-los. É dada pela soma das energias
cinética e potencial: Em = Ec + Ep
Energia Cinética – Energia associada ao movimento. É uma grandeza escalar que depende da
massa e do quadrado da velocidade do corpo:
mv2
Ec = ––––––
2
Professor CARLOS Jennings
Trabalho e Energia
O conceito científico de trabalho nem sempre
coincide com o que se pensa vulgarmente
sobre trabalho (geralmente tido como “qualquer
esforço do corpo ou da mente”).
Para a Física, Trabalho é a medida das transformações de energia causadas por uma força sobre
um sistema. Energia é um conceito muito abrangente e, por isso mesmo, muito abstrato e difícil
de ser definido de um modo preciso. Usando
apenas a experiência do nosso cotidiano, poderíamos conceituar energia como algo que é capaz
de originar mudanças no mundo.
Podemos dizer que a presença de energia num
dado sistema físico encerra a possibilidade
de que se produza movimento. Por exemplo: a
energia armazenada por uma pessoa, a partir
dos alimentos, permite que ela se movimente e
mova outros corpos.
Trabalho
(ττ) de uma força constante – Se uma
→
força F constante atua em uma partícula,
→
produzindo um deslocamento d. O trabalho
realizado por essa força é dado por:
τ =F.d.cos θ
F = módulo da força aplicada ao corpo;
d = módulo do deslocamento;
→
→
θ = ângulo entre F e d.
Unidade de trabalho (SI) – O joule: trabalho
realizado por uma força de 1 newton, ao
deslocar um corpo por 1 metro (1J = 1N . 1m).
Energia Potencial Gravitacional – Energia
armazenada associada à posição do corpo;
pode permanecer armazenada indefinidamente,
ou ser utilizada a qualquer momento na
produção de movimento, ou seja, pode ser
transformada, no todo ou em parte, em energia
cinética: Ep = m.g.h
Energia Potencial Elástica
É a energia armazenada em uma mola
comprimida ou distendida. Matematicamente:
kx2
Epe = –––––, onde k é a constante elástica e x é
2
a deformação da mola (quanto a mola foi comprimida ou distendida).
Teorema da Energia Cinética – O trabalho da
força resultante é igual à variação de energia
cinética: τ = ∆Ec = Efinal − Einicial
Princípio da Conservação da Energia
Mecânica – Uma força é chamada conservativa,
quando pode devolver o trabalho realizado para
vencê-la. Desse modo, o peso de um corpo e a
força elástica são exemplos desse tipo de força.
No entanto a força de atrito cinético, que não
pode devolver o trabalho realizado para vencêla, é uma força não-conservativa, ou dissipativa
(degrada energia mecânica).
Em um sistema no qual só atuam forças conservativas (sistema conservativo), a energia mecânica
se conserva, isto é, mantém-se com o mesmo
valor em qualquer momento, alternando-se nas
suas formas cinética e potencial (gravitacional ou
elástica).
Dependendo do valor de θ, o trabalho de uma
força pode ser:
a) Positivo (trabalho motor) – A força “contribui”
com o deslocamento.
b) Negativo (trabalho resistente) – A força atua
em oposição ao deslocamento.
c) Nulo – A força é perpendicular ao sentido do
deslocamento do corpo.
Importante: o trabalho de uma força perpendicular ao deslocamento é sempre nulo.
Aplicação
Uma pedra de 2kg é abandonada de uma altura
de 8m em relação ao solo. Calcule a energia
cinética e a velocidade de que estará dotada a
pedra ao atingir o solo? (Despreze a resistência
do ar e considere g = 10m/s2).
Aplicação
Um corpo movimenta-se por 10m sobre uma
superfície horizontal sob a ação das forças
constantes indicadas na figura. Calcule o
trabalho de cada uma das forças atuantes no
corpo. Dados: P = 100N; F = 50N; Fat = 10N;
cos 60° = 0,5; cos 90° = 0; cos 180° = −1.
Solução:
a) Ec = Ep ∴ Ec = mgh = 2.10.8 = 160J (ao
atingir o solo, a pedra terá uma energia cinética
que corresponde à energia potencial que tinha
quando iniciou a queda).
2.v2
mv2
b) Ec = –––– ∴ 160 = –––– ∴v =
=12,6m/s
2
2
IMPULSO E MOMENTO LINEAR
→
Um corpo recebe um impulso ( I ) quando é
solicitado por uma força durante um certo
intervalo de tempo.
→
→
∆t
Impulso de uma força constante: I = F∆
– É uma grandeza vetorial (possui módulo,
direção e sentido).
→
– Tem módulo proporcional ao módulo de F
(quanto maior a força, maior o impulso).
→
– Tem sempre direção e sentido iguais aos de F.
Solução:
→
→
a) P e N são perpendiculares ao deslocamento
(θ = 90º):
τP = P.d.cos90° = 100.10.0 = 0
τN = N.d.cos90°→ = 0
b) Trabalho de F (θ = 60°):
τF = F.d.cos60° = 50. 10. 0,5 = 250J (trabalho
motor);
8
Aplicação
Princípio da Conservação do Momento Linear
Sob a ação de uma força resultante constante de
intensidade 20N, um corpo, de 1,0kg, parte do
repouso no instante t = 0. Calcule o módulo do
impulso da resultante, desde t = 0 até t = 5,0s, e
a velocidade final.
– Um dos mais relevantes da Mecânica; pode
ser assim enunciado:
– Num sistema físico isolado de forças
externas (aquele em que a resultante das forças
externas que nele agem é nula), o momento
linear total permanece constante. Então:
→
→
→
→
→
Qtotal = constante ou Qfinal = Qinicial ⇒ ∆Qtotal = 0
Solução:
→
Desafio
Físico
m.vfinal
0,4 . 4,0
Fm∆t = m.vfinal ∴ Fm=–––––– = ––––––––=160N
∆t
1,0 . 10–2
→
I = F∆t ⇒ I = 20.5 = 100Ns
Para calcular a velocidade, lembre-se de que
v = vo + at, sendo vo = 0 e a = F/m:
F
20
v = ––– .t = ––– . 5= 100m/s
m
1
→
Momento linear (Q) – Também chamado de
momentum ou quantidade de movimento, o
momento linear é uma grandeza vetorial dada
→
→
pela expressão: Q = m . v
→
– Tem módulo proporcional ao módulo de v.
– É uma grandeza instantânea (depende da
definição da velocidade vetorial instantânea).
→
– Tem sempre direção e sentido iguais aos de v.
Aplicação
Antônio Farias, pescador do Cambixe, está com
sua canoa no lago dos Reis. Inicialmente, tanto
a canoa como o pescador repousam em relação
à água que, por sua vez, não apresenta
qualquer movimento em relação à Terra. Atritos
da canoa com a água são desprezíveis e, no
local, não há ventos. Num determinado instante,
o pescador atira horizontalmente a sua zagaia
de massa 2,0kg que sai com velocidade de
10m/s. Calcule o módulo da velocidade do
conjunto pescador/canoa, de massa igual a
150kg, imediatamente após o disparo.
Solução:
Relação entre Energia Cinética e Momento
Linear
mv2
Ec = ––––– (I)
2
Sendo o sistema fisicamente isolado:
Q
Q = mv ∴ v = ––– (II)
m
Substituindo (II) em (I):
Q2
Ec = ––––
2m
Teorema do Impulso
→
→
F = ma ( I )
→
→ →
∆v
v – vo
→
a = ––– = ––––––– (II)
∆t
∆t
Substituindo (II) em (I):
→ →
(v – vo)
→
→
→
→
F = ––––––– ∴ F∆t = m v – m vo
∆t
→
→
→
Itotal = Qfinal – Qinicial
→
→
→
→
Qfinal = Qinicial ∴ Qfinal = 0
→
→
→
→
→
Qzagaia + Qconjunto = 0 ∴ Qzagaia = −Qconjunto
Em módulo:
Qzagaia = Qconjunto
mzagaiavzagaia = mconjuntovconjunto
2,10 = 150.vconjunto
vconjunto = 0,13m/s
Exercícios
01. Um astronauta, tendo em suas mãos
um pequeno objeto, encontra-se em
repouso, em uma região do espaço
onde não existe nenhuma atração gravitacional. Nesta situação, ele arremessa
o objeto, aplicando-lhe um impulso de
12N.s. Considere o sistema astronauta+
objeto e assinale, entre as afirmativas
seguintes, aquela que está errada:
O impulso total exercido em um sistema
durante um certo tempo corresponde à
variação do momento linear desse sistema
durante o intervalo de tempo considerado.
Atenção!
Do Teorema do Impulso, pode-se constatar que
impulso e momento linear são grandezas
físicas de mesma espécie, pois a primeira é
dada pela variação da segunda. Por isso,
possuem as mesmas dimensões e podem ser
traduzidas nas mesmas unidades.
a) O astronauta recebe, do objeto, um
impulso de módulo igual a 12N.s.
b) O objeto passa a se deslocar com
uma quantidade de movimento de
12kg.m/s.
c) O módulo da quantidade de
movimento adquirida pelo astronauta
é menor do que 12kg.m/s.
d) A quantidade de movimento do
sistema, antes de o objeto ser
arremessado, era nula.
e) A quantidade de movimento do
sistema, depois de o objeto ser
arremessado, é nula.
Aplicação
Para bater um pênalti, um jogador aplica um
chute na bola, de massa 0,4kg, comunicandolhe uma velocidade horizontal de módulo
4,0m/s. Sabendo-se que, inicialmente, a bola
estava em repouso e que o chute teve duração
de 1,0.10−2s, calcular a intensidade média da
força aplicada pelo pé à bola.
02. (UFMG-MG) Suponha que o motor de
um carro, durante a aceleração, exerça
no veículo uma força constante de
1500N. Admitindo que o carro parta do
repouso e que a força atue durante
6,0s, sendo de 900kg a massa do
carro, a velocidade adquirida no fim
desse tempo será:
Solução:
Considerando a força aplicada pelo pé como a
resultante paralela ao movimento, pelo
Teorema do Impulso:
Itotal = Qfinal – Qinicial
Como a bola estava inicialmente em repouso,
tem-se Qinicial = 0:
Itotal = Qfinal = mvfinal
(I)
No caso, Itotal pode ser calculado por:
Itotal = Fm∆t
(II)
Comparando (I) e (II):
a) 10m/s
c) 36m/s
e) 15km/h
9
b) 10km/h
d) 30m/s
01. Uma partícula de 20kg parte do repouso→
e, sob a ação única da força constante F
de intensidade de 100N, atinge a
velocidade de 72km/h. Determine:
a) a aceleração da partícula;
b) o deslocamento da partícula; →
c) o trabalho realizado pela força F.
02. Um bloco é lançado com uma
velocidade inicial v0 sobre uma
superfície horizontal e, após percorrer
uma distância d, atinge o repouso.
Nessas condições:
a) Houve ou não realização de trabalho?
b) Em caso positivo, que forças
realizaram trabalho? Esse trabalho é
positivo ou negativo?
03. Um corpo de massa 2kg move-se
horizontalmente com uma velocidade de
3m/s. Num dado instante, passa a atuar
nele uma força F, passando a mover-se,
em 3s, com uma velocidade de 7m/s.
Qual foi o trabalho realizado pela força
sobre o corpo? (Sugestão: utilize o Teorema
da Energia Cinética).
04. (Fuvest-SP) Uma bola de 0,2kg é
chutada para o ar. Sua energia
mecânica em relação ao solo vale 50J.
Qual é a sua velocidade quando está a
5m do solo? Dado: g = 10m/s2.
05. Na questão anterior, a que altura em
relação ao solo estaria a bola, se tivesse
a velocidade de 10m/s.
06. Uma pedra de 0,10kg é lançada
verticalmente para cima com energia
cinética de 20J. Qual é a altura máxima
atingida pela pedra, sabendo-se que g =
10m/s2? (Sugestão: utilize o Princípio da
Conservação da Energia Mecânica).
07. (Unicamp-SP) Uma metralhadora
dispara balas de massa 80g com
velocidade de 500m/s. O tempo de
duração de um disparo é 0,01s.
a) Calcule a aceleração média que uma
bala adquire durante um disparo.
b) Calcule o impulso médio exercido
sobre uma bala.
08. Sobre o impulso de uma força,
podemos afirmar que:
a)
b)
c)
d)
é igual à variação da energia cinética;
é uma grandeza escalar;
é uma grandeza termodinâmica;
é igual ao produto da força pela
velocidade;
e) tem a mesma dimensão de
quantidade de movimento.
Desafio
literário
Literatura
revolução do telégrafo.
f) Os jornais, agora com periodicidade regular, fixam-se nos centros culturais.
Professor João BATISTA Gomes
4. CARACTERÍSTICAS
DO REALISMO/NATURALISMO
a) Apego à objetividade – Não há mais espaço para uma literatura com textos prolixos, com descrições exaltadas de paisagens e de personagens.
Realismo e Naturalismo I
1. ASPECTOS GERAIS
c) Crença na razão – A emoção cede lugar
à razão, sugerindo frieza (às vezes crueza) nas relações amorosas.
a) Duração no Brasil – 1881 a 1893.
b) Obra inauguradora do Realismo:
01. Os itens seguintes contêm características de períodos literários brasileiros.
Qual deles foi caracterizado erradamente?
a) Romantismo: nacionalismo extremado,
valorização do índio e da natureza.
b) Arcadismo: linguagem culta,
rebuscada, com antíteses e hipérbatos.
c) Parnasianismo: apego à rima, à
métrica, à perfeição; poesia descritiva,
com ausência de emoções.
d) Realismo: o importante não era a
trama, o enredo em si, mas a
profundidade com que as
personagens eram analisadas.
e) Realismo: análise da realidade sem o
prisma da fantasia e do sonho.
02. Um dos itens seguintes não pode ser
atrelado ao surgimento do RealismoNaturalismo no Brasil. Identifique-o.
a) A cieência e a tecnologia passaram a
influenciar a visão do escritor.
b) A valorização do materialismo, numa
atitude clara de combate ao
subjetivismo e ao misticismo.
c) O crescimento urbano motivou a
formação de uma casta intelectual e,
conseqüentemente, o consumo de
livros.
d) Valorização do conhecimento empírico.
e) Tentativa de atrelar o comportamento
humano à hereditariedade e ao meio.
03. (Desafio do Rádio) O homossexualismo virou tema de obras literárias no
Realismo-Naturalismo. Isso se pode
comprovar no romance:
a)
b)
c)
d)
e)
Dom Casmurro;
O Mulato;
Memórias Póstumas de Brás Cubas;
A Normalista;
O Bom Crioulo.
04. (Desafio da TV) Ambientados em pequenas e desconhecidas cidades da
Amazônia, os romances de Inglês de
Sousa não despertaram a atenção dos
leitores do Sul, onde foram publicados.
Os leitores ainda se deleitvam com fantasias, fugindo à realidade nua e crua
de uma região ainda inexplorada na
literatura brasileira. Cronologicamente,
Inglês de Sousa inaugurou o Naturalismo no Brasil, em 1877, com o romance:
a)
b)
c)
d)
e)
O Bom Crioulo;
O Coronel Sangrado;
Dona Guidinha do Poço;
O Missionário;
O Mulato.
Memórias Póstumas de Brás Cubas
(romance,1881), de Machado de Assis.
d) Materialismo – A literatura passa a exibir
uma visão materialista da vida, do homem
e da sociedade, negando a relação com
Deus.
c) Obras inauguradoras do Naturalismo:
1. O Coronel Sangrado (romance, 1877),
de Inglês de Sousa.
e) Cientificismo – A defesa de que a vida e
as ações dos homens são determinadas
pela ciência é postura radical do Naturalismo.
2. O Mulato (romance,1881), de Aluísio
Azevedo.
d) Mistura – Realismo e Naturalismo misturam-se na literatura brasileira. Não há
coincidência apenas de datas; os temas,
derivados da filosofia de Tobias Barreto,
são comuns às obras dos dois períodos.
f) Determinismo – O Naturalismo constrói
personagens cuja conduta obedece a três
variáveis: a hereditariedade (que explica
as tendências, os caracteres e as patologias), o meio (capaz de determinar o comportamento) e o momento histórico (responsável pelas ideologias).
e) Guerra ao Romantismo – Realismo e
Naturalismo opõem-se radicalmente ao
Romantismo.
g) Problemas patológicos – A literatura passa a retratar temas que chocam a sociedade: homossexualismo, lesbianismo, incesto, taras sexuais, loucura, adultério, racismo, prostituição.
2. ASPECTOS HISTÓRICO-CULTURAIS
a) A burguesia substitui a aristocracia no
poder.
b) A Revolução Industrial traz avanços no
campo da ciência e da tecnologia.
4. AUTORES E OBRAS
c) A ciência é exaltada; apregoa-se a idéia
de que ela é capaz de resolver todos os
problemas da humanidade.
MACHADO DE ASSIS
Origem humilde – O pai é mulato, pintor de
paredes do Morro do Livramento, no Rio de
Janeiro. A mãe (portuguesa) lava roupa para
ajudar nas despesas de casa.
d) As idéias de Darwin (As Origens das Espécies, 1859) são impostas: o meio condiciona todos os seres vivos, deixando
viver apenas os mais fortes. O meio ambiente é capaz de interferir na formação
da matéria e do espírito.
Infância paupérrima – Machado tem uma
infância paupérrima, de menino do morro,
com as dificuldades comuns de uma família
pobre.
e) A teoria do evolucionismo (ou darwinismo)
repercute na Economia, na Filosofia, na
Política e na Literatura.
Órfão – O pai, a mãe e a irmã logo morrem.
Maria Inês, a madrasta, dá-lhe carinhos de
mãe e é quem o alfabetiza, auxiliada por um
padre da Igreja de Lampadosa.
f) O Positivismo nasce na França: prega o
apego aos fatos, rejeitando qualquer teoria metafísica para a existência e a atuação do homem no mundo.
Escola: sonho distante – Maria Inês trabalha na cozinha de uma escola dirigida por
senhoras. Graças a essa atividade, o menino Machado de Assis pode ali se matricular.
A disciplina inclui palmatória e castigos corporais, mas Machado é aluno exemplar, ávido por conhecimento.
g) O mundo torna-se materialista, suplantando o subjetivismo pregado no período
romântico.
h) As Cartas Filosóficas de Voltaire atacam
as instituições do clero e da monarquia.
Isso provoca a mudança da liderança histórica da aristocracia para a burguesia.
Vendedor de balas e doces – No período
em que não está na escola, o garoto pobre,
magro, franzino vende balas e doces (fabricados pela madrasta) nas ruas de São Cristóvão.
3. SITUAÇÃO BRASILEIRA
a) O Positivismo encontra ressonâncias na
Faculdade de Direito do Recife.
Francês na padaria – A proprietária da
padaria do bairro (São Cristóvão) logo
simpatiza com Machado de Assis. Começa,
então, a dar-lhe aulas de francês. A evolução
é espantosa: Machado domina rapidamente
a nova língua. No futuro, vale-se desses
conhecimentos para ser revisor de provas na
Imprensa Nacional.
b) A abolição dos escravos provoca um crescimento urbano inesperado, favorecendo
as atividades artísticas, entre elas a Literatura.
c) Os primeiros imigrantes europeus (principalmente italianos) chegam ao brasil
para substituir a mão-de-obra escrava.
Primeiro emprego – Machado de Assis, já
rapaz, precisaa trabalhar. A Livraria e Tipografia Paula Brito é a mais famosa da época, no
Rio de Janeiro. Ali Machado vai atrás do seu
primeiro emprego. Não sabe fazer nada, mas
quer estar em contato com livros e escritores.
d) A decadência da lavoura açucareira vira
realidade. A lavoura cafeeira toma impulso, favorecendo o aparecimento de novas
comunidades e o aumento dos bens de
consumo.
Aprendiz de tipógrafo – Depois de uma
certa experiência, é admitido na Imprensa
e) A comunicação brasileira experimenta a
10
Nacional como Aprendiz de Tipógrafo. Às
vezes, deixa de fazer o seu trabalho para
entregar-se a leituras. Os colegas logo o
denunciam ao diretor da casa. Nasce,
assim, a amizade com Manuel Antônio de
Almeida, o festejado autor de Memórias de
um Sargento de Milícias.
Desafio
literário
do escritor ainda em vida.
Escritor completo – Poucos autores na literatura brasileira são tão ecléticos quanto Machado. Faz incursões pela prosa (romance, conto,
crônica, teatro, crítica literária e social) e pela
poesia, com sucesso em ambos. Tudo o que
Machado escreve faz sucesso. Mas é, sem
dúvida, no romance e no conto que o escritor torna-se mestre. Ainda vivo, é aclamado
por todos como o maior escritor da literatura
brasileira – título que perdura até hoje.
Revisor – Com a idade de 19 anos,
Machado já tem fama de intelectual e
estudioso: é contratado por Paula Brito para
atuar como revisor de provas na livraria e
editora. Além de dominar o francês,
Machado dá provas de conhecer em
profundidade a língua portuguesa.
OBRAS ROMÂNTICAS
1.
2.
3.
4.
5.
6.
7.
8.
9.
Contos e Crônicas em jornais – Conhecido
no meio intelectual carioca, Machado começa a colaborar em vários jornais e revistas
do Rio de Janeiro, escrevendo contos, crônicas e críticas literárias.
Primeiro livro – Com vinte e cinco anos de
idade, Machado publica o seu primeiro livro:
um volume de poemas intitulado Crisálidas.
A fama, aos poucas, vai-se espalhando – graças à intensa atividade literária registrada nos
jornais e nas revistas.
Crisálidas (1864, poesias)
Falenas (1870, poesias)
Americanas (1875, poesias)
Ressurreição (1872, romance)
A Mão e a Luva (1874, romance)
Helena (1876, romance)
Iaiá Garcia (1878, romance)
Contos Fluminenses (1870, contos)
Histórias da Meia-Noite (1873, contos)
OBRAS REALISTAS
1. Ocidentais (1901, poesia)
2. Memórias Póstumas de Brás Cubas
(1881, romance)
3. Quincas Borba (1891, romance)
4. Dom Casmurro (1899, romance)
5. Esaú e Jacó (1904, romance)
6. Memorial de Aires (1908, romance)
7. Papéis Avulsos (1882, contos)
8. Histórias Sem Data (1884, contos)
9. Várias Histórias (1896, contos)
10. Relíquias da Casa Velha (1906, contos)
Funcionário Público – Em 1867, ingressa no
funcionalismo público, ocupando um cargo
no Diário Oficial. Já goza, então, da admiração e do respeito do público. Já tem fama
de escritor. É conhecido no Rio de Janeiro
como homem sério, inteligente e esforçado.
Primeira e única namorada – Machado conhece Carolina. Moça branca, já na casa dos
trinta, livre de compromissos amorosos, recém-chegada de Portugal, conquista imediatamente o coração do escritor. A paixão tem
o aval do irmão de Carolina, o poeta Xavier
de Novais, mas esbarra no preconceito da
família branca: Machado é mulato.
CONTOS FAMOSOS
1.
2.
3.
4.
5.
6.
7.
8.
9.
Vitória do amor – Machado e Carolina casamse no fim do ano de 1869. Não têm filhos.
Vivem 35 anos um para o outro. Quando ela
morre, em 1904, Machado dedica-lhe um soneto. Veja-o na íntegra:
À Carolina
Querida, ao pé do leito derradeiro,
Em que descansas desta longa vida,
Aqui venho e virei, pobre querida,
Trazer-te o coração do companheiro.
O Alienista
A Cartomante
Um Apólogo
A Missa do Galo
Cantiga de Esponsais
Noite de Almirante
A Igreja do Diabo
O Segredo do Bonzo
Teoria do Medalhão
POEMAS FAMOSOS
1.
2.
3.
4.
5.
Pulsa-lhe aquele afeto verdadeiro
Que, a despeito de toda a humana lida,
Fez a nossa existência apetecida,
E num recanto pôs o mundo inteiro.
Suave Mari Magno
À Carolina
Círculo Vicioso
A Mosca Azul
Soneto de Natal
Círculo vicioso
Trago-te flores, – restos arrancados
Da terra que nos viu passar unidos
E ora mortos nos deixa separados.
Bailando no ar, gemia inquieto vagalume:
“Quem me dera que eu fosse aquela loira estrela
Que arde no eterno azul, como uma eterna vela!”
Mas a estrela, fitando a lua, com ciúme:
Que eu, se tenho nos olhos malferidos
Pensamentos de vida formulados
São pensamentos idos e vividos.
“Pudesse eu copiar-te o transparente lume,
Que, da grega coluna à gótica janela,
Contemplou, suspirosa, a fronte amada e bela”
Mas a lua, fitando o sol com azedume:
Fama ainda em vida – Diferentemente de
outros mulatos da literatura brasileira, Machado não precisa morrer para tornar-se célebre.
A despeito da origem humílima, da cor, da
doença (era epiléptico), vence o talento. Tanto a carreira de escritor, como a de funcionário público, quanto a literária evoluem vertiginosamente. Numa época em que o escritor
não ganha dinheiro, machado sabe dosar a
atividade profissional com a vocação literária.
Além de escritor festejado, torna-se o primeiro presidente da Academia Brasileira de Letras, sem dúvida uma das maiores glórias
“Mísera! Tivesse eu aquela enorme, aquela
Claridade imortal, que toda a luz resume”!
Mas o sol, inclinando a rútila capela:
“Pesa-me esta
brilhante auréola de nume...
Enfara-me esta luz e desmedida umbela...
Por que não nasci eu um simples vagalume?”
11
Caiu no vestibular
01. (FGV) Leia:
Então, no fundo da floresta, troou um
estampido horrível, que veio reboando pelo
espaço; dir-se-ia o trovão, correndo pelas
quebradas da serrania.
Era tarde.
Não havia tempo para fugir; a água
tinha soltado o seu primeiro bramido, e,
erguendo o colo, precipitava-se, furiosa,
invencível, devorando o espaço como um
monstro do deserto.
Peri tomou a resolução pronta que
exigia a iminência do perigo: em vez de
ganhar a mata suspendeu-se a um dos
cipós, e, galgando o cimo da palmeira, aí
abrigou-se com Cecília.
A menina, despertada violentamente
e procurando conhecer o que se passava,
interrogou seu amigo.
– A água!... respondeu ele apontando
para o horizonte.
José de Alencar, O Guarani
Sobre o fragmento acima, afirma-se
que:
1. Enaltece a força da natureza brasileira.
2. Exalta a coragem do silvícola.
3. Refere um símbolo da fusão dos valores
nativos e europeus.
4. “Pronta” (4.o parágrafo), no texto, significa “preparada”.
5. “Monstro do deserto” (3.o parágrafo) e
“A água!” (6.o parágrafo) são duas metáforas.
Assinale a alternativa que contém
duas afirmações INCORRETAS.
a) 1 e 2.
b) 2 e 3.
c) 3 e 4.
d) 1 e 5.
e) 4 e 5.
02. (FGV) Publicados quase simultaneamente, Memórias Póstumas de Brás
Cubas e O Mulato, ambos os romances praticamente inauguram dois movimentos literários no Brasil. Num deles,
predomina a profundidade da análise
psicológica e, no outro, a preocupação com as leis da hereditariedade e
a influência do ambiente sobre o homem.
Esses movimentos foram:
a)
b)
c)
d)
e)
O
O
O
O
O
Modernismo e o Pós-modernismo.
Futurismo e o Surrealismo.
Barroco e o Trovadorismo.
Romantismo e o Ultra-romantismo.
Realismo e o Naturalismo.
Encarte referente ao curso pré-vestibular
Aprovar da Universidade do Estado do
Amazonas. Não pode ser vendido.
Governador
ALVARENGA, Beatriz et al. Curso de
Física. São Paulo: Harbra, 1979, 3v.
Eduardo Braga
Vice-Governador
Omar Aziz
ÁLVARES, Beatriz A. et al. Curso de
Física. São Paulo: Scipicione, 1999, vol. 3.
Reitor
Lourenço dos Santos Pereira Braga
Vice-Reitor
Carlos Eduardo Gonçalves
Pró-Reitor de Planejamento e Administração
Antônio Dias Couto
Pró-Reitor de Extensão e
Assuntos Comunitários
Ademar R. M. Teixeira
Pró-Reitor de Pós-Graduação e Pesquisa
Walmir Albuquerque
Coordenadora Geral
Munira Zacarias
Coordenador de Professores
João Batista Gomes
Coordenador de Ensino
Carlos Jennings
Coordenadora de Comunicação
Liliane Maia
Coordenador de Logística e Distribuição
Raymundo Wanderley Lasmar
Produção
Aline Susana Canto Pantoja
Renato Moraes
Projeto Gráfico – Jobast
Alberto Ribeiro
Antônio Carlos
Aurelino Bentes
Heimar de Oliveira
Mateus Borja
DESAFIO MATEMÁTICO (p. 3)
01. D;
02. D;
03. B;
04. B;
05. C;
06. A;
07. C;
08. A;
09. E;
10. A;
DESAFIO MATEMÁTICO (p. 4)
01. A;
02. C;
03. A;
04. A;
05. E;
06. E;
07. C;
08. A;
DESAFIO MATEMÁTICO (p. 5)
01. D;
02. B;
03. B;
04. B;
05. A;
06. A;
07. D;
08. C;
BIANCHINI, Edwaldo e PACCOLA,
Herval. Matemática. 2.a ed. São Paulo:
Moderna, 1996.
BONJORNO, José et al. Física 3: de olho
no vestibular. São Paulo: FTD, 1993.
CARRON, Wilson et al. As Faces da
Física. São Paulo: Moderna, 2002.
DANTE, Luiz Roberto. Matemática:
contexto e aplicações. São Paulo: Ática,
2000.
GIOVANNI, José Ruy et al. Matemática.
São Paulo: FTD, 1995.
DESAFIO FÍSICO (p. 7)
01. D;
02. C;
Grupo de Reelaboração do Ensino de
Física (GREF). Física 3: eletromagnetismo. 2.a ed. São Paulo: Edusp, 1998.
DESAFIO FÍSICO (p. 8)
2
01. a) 90N e b) 2,5m/s ;
DESAFIO FÍSICO (p. 9)
01. E,C e C;
2
02. a) 3m/s e b) 15N ;
03. V, V, V, V, V e F;
2
04. a) 1,6m/s , b) 16m/s e c)O móvel
continuará em MRU;
DESAFIO GRAMATICAL (p. 10)
01. C;
02. E;
03. D;
04. E;
PERSCRUTANDO O TEXTO (p. 10)
01. C; 02. E; 03. B; 04. D; 05. A;
06. B; 07. C; 08. B; 09. D; 10. A;
CAIU NO VESTIBULAR (p. 11)
01. E; 02. D; 03. A; 04. C;
PARANÁ, Djalma Nunes. Física. Série
Novo Ensino Médio. 4.a ed. São Paulo:
Ática, 2002.
RAMALHO Jr., Francisco et alii. Os
Fundamentos da Física. 8.a ed. São
Paulo: Moderna, 2003.
TIPLER, Paul A. A Física. Rio de Janeiro:
Livros Técnicos e Científicos, 2000, 3v.
Paulo Alexandre
Rafael Degelo
Tony Otani
Editoração Eletrônica
Horácio Martins
Este material didático, que será distribuído nos Postos de Atendimento (PAC) na capital e Escolas da Rede Estadual de Ensino, é
base para as aulas transmitidas diariamente (horário de Manaus), de segunda a sábado, nos seguintes meios de comunicação:
• TV Cultura (7h às 7h30); sábados: reprise às 23h
• Amazon Sat (21h30 às 22h)
• RBN (13h às 13h30) reprise: 5h30 e 7h (satélite)
• Rádio Rio Mar (19h às 19h30)
• Rádio Seis Irmãos do São Raimundo
(8h às 9h e reprise de 16h às 16h30)
• Rádio Panorama de Itacoatiara (11h às 11h30)
• Rádio Difusora de Itacoatiara (8h às 8h30)
• Rádio Comunitária Pedra Pintada de Itacoatiara
(10h às 10h30)
• Rádio Santo Antônio de Borba (18h30 às 19h)
• Rádio Estação Rural de Tefé (19h às 19h30) – horário local
• Rádio Independência de Maués (6h às 6h30)
• Rádio Cultura (6h às 6h30 e reprise de 12h às 12h30)
• Centros e Núcleos da UEA (12h às 12h30)
Postos de distribuição:
•
•
•
•
PAC São José – Alameda Cosme Ferreira – Shopping São José
PAC Cidade Nova – Rua Noel Nutles, 1350 – Cidade Nova I
PAC Compensa – Av. Brasil, 1325 – Compensa
PAC Porto – Rua Marquês de Santa Cruz, s/n.°
armazém 10 do Porto de Manaus – Centro
• PAC Alvorada – Rua desembargador João
Machado, 4922 – Planalto
• PAC Educandos – Av. Beira Mar, s/nº – Educandos
www.uea.edu.br e www.linguativa.com.br
Endereço para correspondência: Projeto Aprovar - Reitoria da UEA - Av. Djalma Batista,
3578 - Flores. CEP 69050-010. Manaus-AM