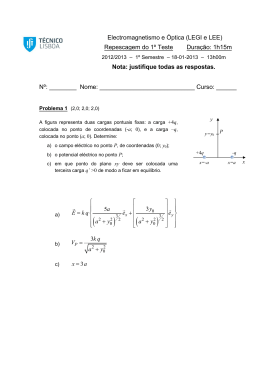
Campo eléctrico – lei de Gauss
As três coroas esféricas condutoras apresentadas na figura são concêntricas e,
inicialmente, estão descarregadas. Após uma carga -Q0 ser colocada na esfera
interior e, a seguir, uma carga +Q0 ser colocada na exterior, determine:
a) O sentido do campo eléctrico entre as coroas I e II.
b) A carga na superfície interior da coroa II.
c) A carga na superfície exterior da coroa II.
d) A carga na superfície interior da coroa III
e) A carga na superfície exterior da coroa III.
f) Esboce o gráfico de E em função de r.
III
II
I
EO - Aula 3
1
As três coroas esféricas condutoras apresentadas na figura são concêntricas e,
inicialmente, estão descarregadas. Após uma carga -Q0 ser colocada na esfera interior e, a
seguir, uma carga +Q0 ser colocada na exterior, determine:
a) O sentido do campo eléctrico entre as coroas I e II.
b) A carga na superfície interior da coroa II.
c) A carga na superfície exterior da coroa II.
d) A carga na superfície interior da coroa III
e) A carga na superfície exterior da coroa III.
f) Esboce o gráfico de E em função de r.
E
-Q0
III
II
I
+Q0 0
-Q0
+Q0
-Q0
a) Para o centro.
+Q0
b) +Q0
f)
c) -Q0
d) +Q0
e) QIIIext= +Q0 + (-Q0) = 0
EO - Aula 3
2
Potencial eléctrico
Considere uma esfera não condutora de raio R com uma carga Q uniformemente
distribuída. Pretende-se determinar o potencial eléctrico V para r < R. Para tal,
calcule:
a)
b)
c)
c)
A carga q’ dentro de uma esfera de raio r.
Use o teorema de Gauss para calcular o campo E em r.
Mostre que V(R)=kQ/R
Calcule V em r < R a partir do campo eléctrico.
a)
b)
ρ=
Q
4
3
πR
3
E  4 r 
2
=
q'
4
3
q
0
πr
q' =
3
Ek
q
r
2

r3
R
3
kQ
R
3
Q
r
Potencial eléctrico
Considere uma esfera não condutora de raio R com uma carga Q uniformemente distribuída.
Pretende-se determinar o potencial eléctrico V para r < R. Para tal, calcule:
a)
b)
c)
c)
A carga q’ dentro de uma esfera de raio r.
Use o teorema de Gauss para calcular o campo E em r.
Mostre que V(R)=kQ/R
Calcule V em r < R a partir do campo eléctrico.
c)
 V  Vb  Va 
U
q
b
   E  dl
a
R
kQ
r
R3 r
V( R )  V( r )    E( r )dr  
kQ

2R
V( r ) V( R )
kQ
2R
3
3


R2  r 2
R2  r 2



R
rdr
Potencial eléctrico
Um condutor esférico de raio R1 é carregado até atingir o potencial de 20 kV.
Quando é ligado por um fio a outro condutor esférico muito distante, o seu
potencial baixa para 12 kV. Determine o raio da segunda esfera.
Admitamos que a carga inicial na
esfera 1 é Q=Q1+Q2.
O seu potencial é 20 kV =
k  Q1 + Q2 
R1
NOTA: se as esferas estivessem próximas, o potencial seria diferente. Assim, como
estão muito distantes, a carga de cada esfera não influencia o potencial da outra.
Após a ligação:
V1 = V2  12kV
k Q1
V1 =
R1
Q1 =
k Q2
R2
Q2 =
V2 =
12 kV  R1
k
12 kV  R2
EO - Aula 3
k
5
Potencial eléctrico
Um condutor esférico de raio R1 é carregado até atingir o potencial de 20 kV.
Quando é ligado por um fio a outro condutor esférico muito distante, o seu
potencial baixa para 12 kV. Determine o raio da segunda esfera.
Substituindo em 20 kV =
k  Q1 + Q2 
R1
 12 kV  R1 12 kV  R2 
k
+

k
k
 R2 


20 kV =
= 12 kV +12 kV 

R1
R
 1
2
R2 = R1
3
EO - Aula 3
6
Potencial eléctrico
Uma carga pontual q está à distância x do centro de uma esfera condutora de raio
R , mantida ao potencial V0.
a) Qual a carga na esfera de raio R ?
b) Qual a carga que a esfera adquire se for ligada à massa ?
c) Qual a força entre a esfera e a carga na alínea b) ?
a)
A carga Q na esfera pode ser obtida a
partir do potencial V0 dado:
q
Q
V0  k  k
x
R
b)
qR

Q   V0  k 
x k

Q?
R
q
x
Se a esfera for ligada à massa (terra) o seu potencial é V0=0. A esfera
vai absorver, da terra, a carga necessária para manter este potencial:
V0  0
R
Q  q
x
EO - Aula 3
7
V0
Potencial eléctrico
Uma carga pontual q está à distância x do centro de uma esfera condutora de raio
R , mantida ao potencial V0.
a) Qual a carga na esfera de raio R ?
b) Qual a carga que a esfera adquire se for ligada à massa ?
c) Qual a força entre a esfera e a carga na alínea b) ?
c)
qQ
F k 2
x
R
Q  q
x
Q?
R
q
x
q2 R
F  k 3
x
EO - Aula 3
8
V0
Potencial eléctrico
Quando a amplitude do campo eléctrico no ar é maior do que 3x106 N/C, o ar
torna-se ionizado e começa a conduzir electricidade (disrupção dieléctrica).
Uma carga de 18 C é colocada numa esfera condutora. Determine qual o raio
mínimo que essa esfera deve ter para se evitar a disrupção.
Q
Campo eléctrico no exterior de uma
esfera condutora carregada:
rR
Emáx = k
E=
Q
2
Rmin
kQ
r
2
E=k

Q
r2
kQ
R
r
R2
Q
Rmin = k
 0, 23m
Emáx
EO - Aula 3
9
Potencial eléctrico
Duas coroas esféricas metálicas isoladas, concêntricas, têm, respectivamente,
raio R2=2R e carga Q2=2Q e raio R3=3R e carga Q3=3Q. Coloca-se no centro
comum uma esfera metálica de raio R1=R, sem carga. Se se ligar esta esfera à
terra, determine a carga q que passa pelo condutor de ligação.
1  Q1 Q2 Q3  q  2Q

 
V R1  


4 0  R1 R2 R3  4 0 R
1  Q1  Q2 Q3 
1 q



V R 2  



2
Q




4 0  R2
R3  4 0 R  2

Q1  Q2  Q3
1 q  5Q
V R3  

4 0
R3
4 0 R 3
1
EO - Aula 3
10
Potencial eléctrico
Duas coroas esféricas metálicas isoladas, concêntricas, têm, respectivamente, raio R2=2R e
carga Q2=2Q e raio R3=3R e carga Q3=3Q. Coloca-se no centro comum uma esfera metálica
de raio R1=R, sem carga. Se se ligar esta esfera à terra, determine a carga q que passa pelo
condutor de ligação.
V  R1  
V R1   0
1
4 0
 q  2Q 
q  2Q
EO - Aula 3
11