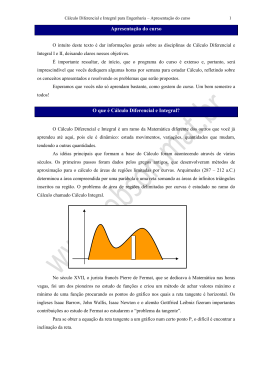
PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL
Faculdade de Matemática - Departamento de Matemática
Cálculo I - 2006/1
APROXIMAÇÃO LINEAR LOCAL E DIFERENCIAIS
Uma curva fica muito perto de sua reta tangente nas proximidades do ponto de tangência.
Podemos usar a reta tangente em (x0, f(x0)) como aproximação para a curva y = f(x) quando x está
próximo de x0.
Uma equação dessa reta tangente é
y = f (x0) + f´(x0).( x-x0 )
A aproximação f(x) ≈ f(x0) + f´(x0). (x-x0) é chamada de aproximação linear local de f em x0 ou
aproximação de f pela reta tangente em x0.
A função linear cujo gráfico é essa reta tangente, isto é, L(x) = f(x0) + f´(x0).( x-x0) é chamada
linearização de f em x0.
Exemplo: Encontre a linearização da função f ( x ) =
números
3,98 e
x + 3 em x0 = 1 e use-a para aproximar os
4,05
DIFERENCIAIS
A idéia por trás da aproximação linear é algumas vezes formulada com a terminologia e notação
de diferenciais. Se y = f(x), onde f é uma função diferenciável, então a diferencial dx é uma
variável independente, isto é, pode ser dado um valor real qualquer a dx . A diferencial dy é então
definida em termos de dx pela equação dy = f´(x) dx.
Assim dy é uma variável dependente, ela depende dos valores de x e dx.
O significado geométrico de diferencial está na figura.
y
R
f ( x + ∆x)
f (x)
Q
∆y
P
dy
S
x
x + ∆x
x
Seja P ( x, f ( x )) ) e Q ( x + ∆x, f ( x + ∆x ) ) pontos sobre o gráfico de f e façamos dx = ∆x
A variação correspondente em y é ∆y = f ( x + ∆x ) − f ( x ). A inclinação da reta tangente PR é
f´(x). Assim a distância direta de S a R é f´(x) dx = dy.
Conseqüentemente , dy representa a distância que a reta tangente sobe ou desce ( a variação na
linearização) enquanto ∆y representa a distância que a curva y= f(x) sobe ou desce quando x
varia de uma quantidade ∆x .
1
Exercícios
1) Compare os valores de ∆y e dy se y = f(x) = x3 + x2 –2x –1 e x variar
a) de 2 para 2,05
b) de 2 para 2,01
2) O raio de uma esfera tem 21cm, com um erro de medida possível de no máximo 0,05. Qual é o
erro máximo cometido ao usar esse valor de raio para computar o volume da esfera? Determine
também o erro relativo.
3) Encontre a linearização da função f(x) = ln (x) em a=1
4) Encontre a aproximação linear da função f ( x ) = 3 1 + x em a=0 e use-a para aproximar os
números
3
0,95 e 3 1,1 . Ilustre fazendo os gráficos de f e a reta tangente.
5) Verifique a aproximação linear dada em a=0.
a) ex ≈ 1+x
b) 1/ ( 1+2x)4 ≈ 1-8x
6) A circunferência de uma esfera mede 84cm, com um erro possível de 0,5 cm.
a) use diferenciais para estimar o erro máximo na área superficial calculada. Qual o erro relativo?
b) use diferenciais para estimar o erro máximo no volume calculado. Qual o erro relativo?
Resolva mais exercícios no ANTON, V1, p.217
PLANO TANGENTE E DIFERENCIAL TOTAL DE FUNÇÕES DE DUAS VARIÁVEIS
O plano tangente a uma superfície em um ponto P0, é o plano que contém as retas tangentes a
todas as curvas sobre a superfície que passam por P0. Prova-se que se P0 (x0, y0, z0) é um ponto
qualquer sobre a superfície z = f (x,y) e se f (x,y) for diferenciável em (x0,y0 ), então a superfície
tem um plano tangente em P0 e esse plano tem equação
fx ( x0,y0) ( x-x0) + fy ( x0,y0) (y-y0) – ( z-z0) =0
Exemplo: Determine o plano tangente ao parabolóide elíptico z = 2x2 + y2 no ponto (1,1,3).
APROXIMAÇÃO LINEAR LOCAL
A função linear cujo gráfico é o plano tangente, ou seja
L(x, y) = f( x0,y0) + fx ( x0,y0) ( x-x0) + fy ( x0,y0) (y-y0) é chamada linearização de f em (x0,y0).
A aproximação da função f pela função linear L
f(x,y) ≈ f( x0,y0) + fx ( x0,y0) ( x-x0) + fy ( x0,y0) (y-y0) é chamada de aproximação linear local da f
ou aproximação de f pelo plano tangente em (x0,y0 , f ( x0,y0))
Geometricamente esta aproximação nos diz que a variação de z ao longo da superfície e a
variação de z ao longo do plano tangente são aproximadamente iguais quando ∆x e ∆y são
pequenos.
2
DIFERENCIAIS
Analogamente ao que foi visto para função de uma variável, se z = f(x, y) é uma função de duas
variáveis , definiremos os diferenciais dx e dy como variáveis independentes ; ou seja podem ter
qualquer valor. Então o diferencial dz, também chamado de diferencial total, é definido por dz =
fx (x,y) dx + fy (x,y) dy .
Assim dz é a variação de z, ao longo do plano tangente à superfície de equação z = f( x,y) em (
x0,y0,z0), produzida pelas variações dx e dy em x e y respectivamente.
Já ∆z representa a variação de z ao longo da superfície, produzida pelas variações de ∆x e ∆y
em x e y, isto é, ∆z = f ( x + ∆x, y + ∆y ) − f ( x, y )
Exercícios
7) Determine a aproximação local de f ( x, y ) = x 2 + y 2 em um ponto (x0, y0).
Use a aproximação linear que você encontrou para aproximar f (3,04; 3,98).
8) Seja z = 4.x3.y2. Determine dz
9) O raio de um cilindro circular reto é medido com um erro, no máximo de 2%, e a altura é
medida com um erro de no máximo 4%. Aproxime o erro percentual máximo no volume V
calculado por essas medidas.
10) Confirme que a fórmula enunciada é a aproximação linear local em (0,0).
a) ex sen(y ) ≈ y
b)
2x + 1
y +1
≈ 1 + 2x –y
11) Suponha que T (x, y) é a temperatura em Fahrenheit em um ponto (x,y) sobre uma placa de
metal.
Dado que T ( 1, 3) = 93º F, Tx ( 1,3) = 2º F/cm e Ty ( 1,3) = –1º F/cm, use uma aproximação linear
local para estimar a temperatura no ponto T ( 0,98; 3,02).
12) Utilize diferencial para estimar a quantidade de metal em uma lata cilíndrica fechada de 10cm
de altura e 4cm de diâmetro se o metal das tampas de cima e de baixo têm 0,1 cm de espessura e
o das laterais tem espessura de 0,05cm.
Leia a secção 3.6 e resolva mais exercícios no ANTON, V1 , p. 210
Leia a secção 6.5 e resolva mais exercícios no ANTON, V2 , p. 352.
Respostas
1) a) ∆y = 0,717625
b) ∆y = 0,140701
dy = 0,7
dy = 0,14
2) dV = 88,2π cm 3
erel =
dV
≈ 0,7%
V
3) f ( x ) ≈ x − 1
3
4)
3
0,95 ≈ 0,9834
6) a) dA =
84
π
cm 2
3
1,1 ≈ 1,033
dA
≈ 1,19%
A
erel = 1,7%
erel =
b) dV = 176,4cm 3
7) L( x, y ) =
x02 + y 02 +
x0
x +y
2
0
2
0
( x − x0 ) +
y0
x + y 02
2
0
f (3,04;3,98) ≈ 5,008
8) dz = 12 x 2 y 2 dx + 8 x 3 y dy
9)
dV
= 8%
V
11) T (0,98;3,02) ≈ 92,94
12) 1,8πcm 2
4
( y − y0 )