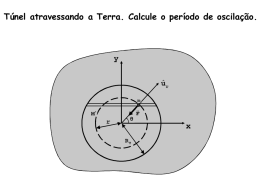
www.fisicaexe.com.br
Uma partícula com carga q 1 = 1 µC e massa 5 g é lançada na direção radial de outra
partícula, com carga q 2 = 6 µC e fixa no espaço, a velocidade de lançamento é de 12 m/s de
uma distância de 0,3 m. Determinar a que distância da partícula fixa a partícula lançada vai ter
velocidade nula. Considere o meio o vácuo onde a constante eletrostática vale
Nm2
k 0 = 9 .10 9
e despreze efeitos gravitacionais.
C2
Dados do problema
•
•
•
•
•
•
carga 1:
carga 2:
velocidade inicial da carga 1
velocidade final da carga 1
distância inicial da carga 1:
massa da carga 1:
•
constante eletrostática do vácuo:
q 1 = 1 µC;
q 2 = 6 µC;
v i = 12 m/s;
v f = 0;
d i = 0,3 m;
m=5g
:
:
k 0 = 9 .10 9
Nm2
C2
Esquema do problema
A carga 2 é positiva
(q 2 > 0), então ela gera um
campo
elétrico
de
afastamento
(apontando
para fora da carga). A carga
1 é lançada radialmente
então segue uma linha de
campo, como também é
positiva (q 1 > 0) e como
r
r
F = q E a força elétrica
figura 1
sobre a carga 1 tem a
mesma direção e sentido do
campo elétrico, como a carga é lançada no sentido oposto ao campo ela sofrerá uma
desaceleração devido a força elétrica até parar.
Solução
Em primeiro lugar vamos transformar a unidade de massa dada em gramas para
quilogramas usado no Sistema Internacional (S.I.).
m = 5 g = 5 . 10 − 3 kg
Inicialmente a partícula 1 no ponto A está
sob o potencial (V A) deste ponto, ao se deslocar
para o ponto B passa para um potencial (V B),
neste deslocamento há a realização de um
trabalho dado por
(
ℑ BA = q 1 V A − V B
)
(I)
Pelo Teorema da Energia Cinética da
Mecânica Clássica o trabalho para um corpo ir A
até B é dado pela variação da Energia Cinética
(figura 2)
ℑ BA
=
m v f2
2
1
figura 2
−
m v i2
2
(II)
www.fisicaexe.com.br
Igualando as expressões (I) e (II), temos
(
)
q 1 V A − VB =
m v f2
2
−
m v i2
2
(III)
O potencial gerado pela carga 2 nos pontos A e B é calculado por
VA = k 0
q2
di
VB = k 0
e
q2
df
(IV)
substituindo as expressões (IV) em (III), obtemos

q2
q2
q1  k 0
− k0

df
di

 m v f2 m v i2
=
−

2
2

colocando k 0 q 2 em evidência no lado esquerdo da igualdade e sendo v f = 0 do lado direito
 1
m v i2
1 
q1 k 0 q 2 
=−
−
 di df 
2


m v i2
1
1
−
=−
di df
2 k 0 q1 q 2
m v i2
1
1
=
+
d f d i 2 k 0 q1 q 2
substituindo os valores numéricos dados no problema. temos
5 .10 − 3 .12 2
1
1
=
+
df
3 .10 −1 2 . 9 . 9 .1.10 − 6 . 6 .10 − 6
1
10 5 .144
=
+
3
108
df
1
10 720
=
+
df
3 108
simplificando a fração
720
108
dividindo o denominador e numerador por 36, temos
720 : 36 20
=
108 : 36
3
1
10 20
=
+
3
3
df
1
30
=
3
df
df =
3
30
d f = 0,1 m
2