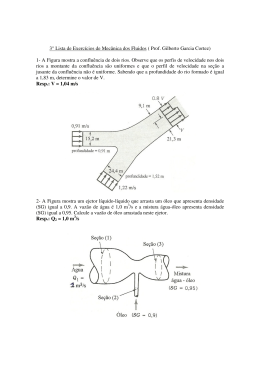
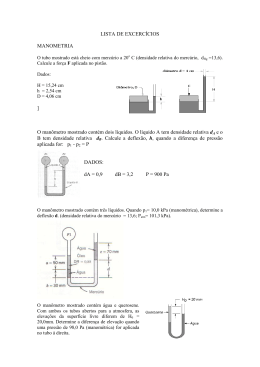
6° Lista de Exercícios de Mecânica dos Fluidos ( Prof. Gilberto Garcia Cortez)
1- Água escoa num tubo com diâmetro constante e apresenta as seguintes características:
(a) Pa = 2,2 bar e za = 17,3 m e na seção (b) Pb = 2,0 bar e zb = 20,8 m. O sentido do
escoamento é de (a) para (b) ou de (b) para (a)? Justifique sua resposta.
Resp.: hl = -1,46 m (impossível!). O fluxo é de (b) para (a), em declive.
(b)
?
(a)
2- Glicerina a 200C escoa para cima num tubo (diâmetro = 75 mm). A velocidade na linha
de centro do tubo é igual a 1,0 m/s. Determine a queda de pressão e a perda de carga
distribuída em metros sabendo que o comprimento do tubo é igual a 10 m.
(∆P − γ LsenΘ)D 2
Dado: ρglicerina = 1260 kg/m3; µglicerina = 1,5 N.s/m2; v =
32 µ L
Resp.: ∆P = 166 kPa; hl = 3,43 m
10 m
3- Óleo (peso específico = 8900 N/m3, viscosidade dinâmica = 0,10 N.s/m2) escoa no tubo
mostrado. O diâmetro do tubo é igual a 23 mm e um manômetro diferencial em U é
utilizado para medir a queda de pressão no escoamento. Qual é a variação da pressão entre
as tomadas de pressão do manômetro diferencial? Qual é o máximo valor de h para que o
escoamento de óleo ainda seja laminar? Para fluxo laminar, adote Re = 2100.
Resp.: ∆P = 30,47 kPa; h = 0,51 m
0,5 m
Óleo
23 mm
h
SG = 7,0
4- Óleo (densidade = 0,87 e ν = 2,2.10-4 m2/s) escoa no tubo vertical mostrado na Figura. A
vazão de óleo é 4,0.10-4 m3/s. Determine a leitura do manômetro h.
(∆P + γ L ) π D 4
Dado: Q =
128 µ L
Resp.: h = 18,5 m
10 m
10 m
5- Determine a leitura do manômetro, h, da Figura sabendo que o escoamento é para cima
(isto é, ao contrário do mostrado na Figura anterior).
(∆P − γ L ) π D 4
Dado: Q =
128 µ L
Resp.: h = -18,5 m
6- Ar escoa no tubo mostrado na Figura (diâmetro e comprimento iguais a 2,7 e 610 mm).
Determine o fator de atrito sabendo que h = 43 mm quando a vazão, Q, é igual a 5,4.10-5
m3/. Compare o resultado com o fornecido por f = Re/64. O escoamento é laminar ou
turbulento?
Dado: ρar = 1,269 kg/m3; νar = 1,36.10-5 m2/s
Resp.: f ≅ 0,0287
h = 43 mm
Água
2,7 mm
Ar
Ar
610 mm
7- Água escoa (vazão = 0,04 m3/s) num tubo (diâmetro = 0,12 m) conectado a uma
contração abrupta que apresenta seção de descarga com diâmetro igual a 0,06 m. Determine
a perda de pressão do escoamento na contração. Quanto desta diferença de pressão é devida
as perdas e quanto é devido a variação de energia cinética? Dado: ρágua = 999 kg/m3.
Resp.: P1 – P2 = 133 kPa ( 39,7 kPa é devido as perdas e 93,0 kPa é devido ao aumento
da energia cinética)
D1 = 0,12 m
D2 = 0,06 m
Q = 0,04 m3/s
8- A Figura mostra que a instalação de um redutor de pressão em chuveiros elétricos pode
diminuir os consumos de água e energia. Admitindo que a pressão no ponto (1) permanece
constante e que todas as perdas, exceto a causada pelo “redutor de pressão”, forem
desprezadas, determine o valor do coeficiente de perda (baseado na velocidade no duto)
para que o redutor de pressão diminua a vazão pela metade. Despreze os efeitos da
gravidade.
Resp.: K ≅ 8,0
9- Água escoa no tubo mostrado na Figura. Determine o coeficiente de perda para o
escoamento através da tela.
Resp.: KTela = 0,176
10- Ar escoa na tubulação mostrada na Figura. Determine a vazão se as perdas localizadas
forem desprezíveis e o fator de atrito em cada tubo for igual a 0,020. Admita que o
escoamento de ar é incompressível. Determine a vazão de substituirmos o tubo com 12,7
mm por um com 25,4 mm de diâmetro. Analise se a hipótese de escoamento incompressível
é razoável.
Resp.: - a) Q ≅ 3,1.10-3 m3/s; b) Q ≅ 1,2.10-2 m3/s c) ρ3/ρ0 ≅ 0,967