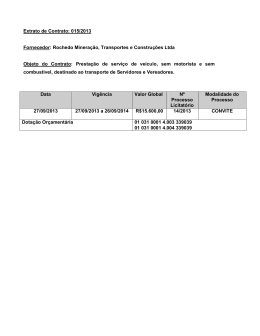
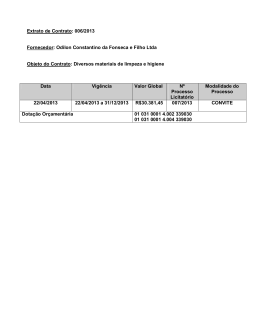
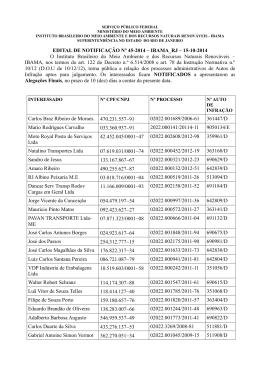
Um estudo introdutório do método do Gradiente para minimização de
funções de uma ou várias variáveis
Juliane Carla Lopes Prado*
André Luís Machado Martinez
Universidade Tecnológica Federal do Paraná, campus Cornélio Procópio, PR
Avenida Alberto Carazzai, 1640 CEP 86300-000
E-mail: [email protected]
RESUMO
Neste trabalho realizamos um estudo introdutório do método Gradiente para a determinação de
mínimo de funções, inicialmente consideramos apenas funções de uma variável real, com o
intuito de observar o comportamento do método, posteriormente consideramos funções de
várias variáveis, testes numéricos foram realizados e implementações foram feitas no software
MatLab.
Palavras-chave: Método de Gradiente, Funções de uma e várias variáveis, Otimização,
Problemas irrestritos, MatLab
MÉTODO GRADIENTE
A otimização numérica, ou programação matemática, refere-se ao estudo de problemas
nos quais se busca determinar um mínimo ou máximo de uma função através da escolha
sistemática dos valores de variáveis reais ou inteiras em um determinado conjunto admissível.
Como a otimização possui inúmeras aplicações em engenharia, administração, logística,
biologia e outras diversas áreas do conhecimento, o estudo de métodos de otimização é um
campo extenso na matemática aplicada. Temos como vantagens diminuir o tempo dedicado ao
projeto, possibilitar o tratamento simultâneo de uma grande quantidade de variáveis e restrições
de difícil visualização gráfica e/ou tabular, possibilitar a obtenção de algo melhor, obtenção de
soluções não tradicionais, menor custo e como limitações podemos ter, dependendo da
quantidade de variáveis e operações, um grande custo computacional e talvez erros na
programação ocasionando a demora na execução do problema.
Neste trabalho estamos desenvolvendo um estudo do método Gradiente (sugerimos [1],
[2], [3], [4], [5] e [7]) ou método do declive máximo, onde a direção de descida é determinada
pelo oposto da direção da derivada. Com o auxilio do software MatLab (www.mathworks.com)
implementamos o método do gradiente para minimizar funções, primeiramente para funções de
apenas uma variável real, onde nosso objetivo é de encontrar uma raiz para a equação
, para
, continuamente diferenciável. Dada uma aproximação
para um mínimo de
o método Gradiente consiste basicamente em estimar
com uma busca linear na
direção
, assim em um primeiro momento definimos simplesmente
, desta forma obtemos a sequência do método Gradiente puro. Programamos o método
Gradiente Puro para funções de uma variável real no MatLab, a condição de parada utilizada
ou atingir 200 iterações, testes foram realizados e os resultados são
apresentados a seguir:
Função
)
inical
Convergiu
final
0.0001
0
Não
200
-0,0001
-1
0.0001
0
Não
200
-1,5708
-1
* Bolsista de Iniciação Científica PIBIC/CNPq
234
0.0001
0
Não
200
-Inf
-Inf
0.0001
0
Sim
43
-1
-0,5
Tabela 1: Resultados obtidos com o Algoritmo.
De posse dos resultados podemos observar a fragilidade do método Gradiente e seu
comportamento voraz por decréscimo ao se deparar com funções ilimitadas em algumas
direções. Com o intuito de melhorar o desempenho do método incluímos uma busca linear na
direção de
ou seja, agora
, onde
é obtido pelo
algoritmo do retrocesso (recomendamos [2], [3]) e cumpre a condição de Armijo
<
2[
]2.
Repetimos os testes com o Método Gradiente com busca linear, os resultados são
apresentados na tabela a seguir:
Função
Convergiu
inical
)
final
0.0001
0
Sim
3
0
-1
0.0001
0
Não
200
-1,5708
-1
0.0001
0
Não
200
1,8645
-0,9474
0.0001
0
Sim
43
-1
-0,5
Tabela 2: Resultados obtidos com o Algoritmo retificado.
Podemos observar que o método passou resolver um numero maior de problemas e que
seu desempenho passou a ser mais consistente. Após o estudo com funções de uma variável real
passamos a considerar funções de varias variáveis reais a valores reais. A sequência do método
Gradiente puro a ser considerada agora é
, programamos o método no
MatLab, na tabela a seguir apresentamos alguns testes realizados em exemplos retirados de [6] e
[8].
Função
inical
Convergiu
final
0.0001
[0 0]
Não
200
[-Inf 2,65]
NaN*
0.0001
[0 0]
Não
14
NaN*
NaN*
0.0001
[0 0]
Sim
1
[0 0]
-2
0.0001
[0 0 0]
Sim
1
[0 0 0]
0
Tabela 3: Resultados obtidos com o Algoritmo de varias variáveis.
*NaN: Not a Number, tal valor aparece quando é obtido operações matemáticas indefinidas
como ou ∞-∞.
Assim como feito para funções de uma variável real pretendemos aumentar a robustez
do método, incluímos uma busca linear na direção de
ou seja, agora
, onde
é obtido pelo algoritmo do retrocesso e cumpre a condição de
* Bolsista de Iniciação Científica PIBIC/CNPq
235
Armijo
.
Repetimos os testes com o Método Gradiente com busca linear, os resultados são
apresentados na tabela a seguir:
Função
inical
Convergiu
final
0.0001
[0 0]
Sim
14
[1 1]
-4
0.0001
[0 0]
Não
15
NaN
NaN
0.0001
[0 0]
Sim
31
[6 2]
-26
0.0001
[0 0 0]
Sim
1
[0 0 0]
10
Tabela 4: Resultados obtidos com o Algoritmo de varias variáveis com busca linear.
Podemos observar que o método passou resolver um numero maior de problemas e que
seu desempenho passou a ser mais consistente com a inclusão da busca linear.
CONCLUSÃO
O desenvolvimento dos estudos do método Gradiente para funções de várias variáveis
ainda encontra-se no inicio, mas já podemos obter conclusões sobre o comportamento do
método. Observamos como a inclusão do retrocesso tornou o método mais robusto para os
exemplos testados, também notamos como o método é sensível à escolha do ponto inicial o que
em muitos exemplos definia a convergência ou não do método, por este motivo realizamos os
testes apenas com ponto inicial nulo. Pretendemos testar mais exemplos e aprofundar os estudos
sobre a convergência do método, bem como testar outras possibilidades de busca linear como o
algoritmo da seção áurea ao invés do retrocesso.
Referências
[1] Jorge Nocedal, Stephen J. Wright, Numerical Optimization. SPRINGER, 2006.
[2] A. FRIDLANDER, Elementos de Programação não Linear, Editora Unicamp,1994.
[3] J. M. Martínez, S. A. Santos, Métodos Computacionais de Otimizaçãp -IMPA XX
Colóquio Brasileiro de Matemática - 1995.
[4] R. Fletcher, Practical Methods of Optimization, 2nd ed. , John Wiley Sons,1987.
[5] H. L. Guidorizzi, Cálculo. Vol. 1, Ed. LTC, 5ª edição, 2001.
[6] H. L. Guidorizzi, Cálculo. Vol. 2, Ed. LTC, 5ª edição, 2001.
[7] James Stewart, Cálculo. Vol. 1. São Paulo: Pioneira Thomson Learning, 2005.
[8] James Stewart, Cálculo. Vol. 2. São Paulo: Pioneira Thomson Learning, 2005.
* Bolsista de Iniciação Científica PIBIC/CNPq
236