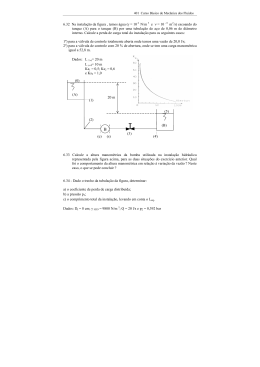
Aula 10 de FT
Primeiro semestre de 2014
1. A água escoa por um tubo cuja seção 1 tem
uma área igual a 1140,1 cm² (DN = 16” aço
40 com Dint = 381 mm) para uma seção 2
cuja área é igual a 509,1 cm² (DN = 10” aço
40 com Dint = 254,5mm). Sabendo que em 1
a pressão é de 4,5 kgf/cm² e a elevação
90m, e que em 2 a pressão é de 3,38
kgf/cm² com uma elevação de 65m, calcule
a vazão em litros por segundo, sabendo que
a perda de carga entre as seções 1 e 2 é
igual a 26,2m.
Dado: g = 9800N/m³
H1  H 2  H p
1 2
p1 v12
p 2 v 22
z1 

 z2 

 Hp
1 2
g 2g
g
2g
4,5  10 4  9,8 v12
3,38  10 4  9,8 v 22
90 

 65 

 26,2
9800
19,6
9800
19,6
v 22  v12  196  I 
v1  A1  v 2  A 2  v1  1140,1  v 2  254,5  v 2  4,48  v1
 v 22  20,07  v12  II
De (II) em (I), temos :
20,07  v12

v12
196
m
 196  v1 
 3,21
19,07
s
Q  3,21  1140,1  10
4
m3
L
 0,366
 366
s
s
2. De uma pequena barragem, parte uma canalização de 250 mm de diâmetro interno,
com poucos metros de extensão, havendo depois uma redução para 125 mm; do
tubo de 125 mm, a água passa para a atmosfera sob forma de jato. A vazão foi
medida e encontrando-se 125 L/s. Sabendo que a perda de carga total é
aproximadamente igual a 2,7 m, pede-se calcular:
a. a altura H de água na barragem;
b. a pressão na seção 1 nas escalas efetiva e absoluta, sabendo que v1 não é nula
e que a perda de carga de 0 a 1 é igual a 0,93m;
c. a potência bruta do jato.
Dados: peso específico da água igual a 9800 kg/m³ e pressão atmosférica local igual a
95200 N/m².
a )  H 0  H 2  H p total
p 0 v 02
p 2 v 22
z0 

 z2 

 H p total
g
2g
g
2g
PHR adotado no eixo passando por 1 :
v 22
H0000
 2,7
2  9,8
Q  v 2  A 2  125  10  3
v2 
4  125  10  3
  0,1252
  0,1252
 v2 
4
m
 10,2
s
10,2 2
H
 2,7  8m
19,6
b)  H 0  H1  H p
0 1
mesmo PHR, resulta :
p1
v12
80

 0,93
9800 19.6
Q  v1  A1  125  10  3
v1 
4  125  10  3
  0,252
  0,252
 v1 
4
 2,55
m
s
2


p1
2,552
2
,
55
8
 0,93  p1  9800   8 
 0,93 


9800
19,6
19
,
6


p1  66043,7
N
m
2
 66043,7 Pa
c) A potência bruta do jato que será representada por N2
energia total em 2 E T 2

 ET2  G  H2
peso
G
Dividindo ambos os membros pelo tempo, resulta :
ET2 G  H2

t
t
ET2
 N2
t
G  H2 G
G
peso
  H2  
 definição de vazão em peso(QG )
t
t
t
tempo
H2 
2

p
v
2
 N 2  QG  H 2  QG   z 2 
 2

g
2g 

G
m
m massa
QG   g  

 definição de vazão em massa(Qm )
t
t
t
tempo
m
 QG  g  Q m  g 
t
Por outro lado, evocando o conceito de massa específica, temos:
massa
m
 m   V
volume V
m
V
QG  g  Q m  g   g     g  Q
t
t
2

p
v
 N2  g  Q  H2  g  Q   z2  2  2 

g
2g 

2
10
,
2
3 

N 2  9800  125  10   0  0 


19
,
6


3
Nm J
 N  m 
N 2    3      m 
 W
s
s
 m   s 
 N 2  6502,5W

3. Uma tubulação vertical
de 150 mm de diâmetro
apresenta,
em
um
pequeno trecho, uma
seção contraída de 75
mm, onde a pressão é
de 10,3 mca. A três
metros acima desse
ponto, a pressão elevase para 14,7 mca.
Calcular as velocidades
e a vazão sabendo que o
coeficiente de vazão (Cd)
é igual a 0,95.
4. Considerando que no ponto S do sifão da figura a pressão
não deve cair abaixo de 32 kPa (abs) e que para esta
pressão limite a perda de carga de (A) a (S) é 0,300 m e de
(S) a (B) é 0,377 m, calcule:
a. a velocidade média do escoamento;
b. a máxima altura do ponto S em relação ao ponto (A)
Dados: patm = 100 kPa; gágua = 9800 N/m³
Os exercícios 4 e 3 ficam para
atividade extra que deve ser
entregue até 26/04/2012 através
do e-mail :
[email protected]
5. O conduto da figura tem diâmetro interno igual a 100 mm e a pressão no
manômetro é pm = 0,24 kgf/cm². As perdas de carga entre as seções 1 e 2 e
entre as seções 4 e 5 são desprezíveis. O fluido é a água com peso específico
igual a 9800N/m³. Determinar:
a. a vazão;
b. a perda de carga na tubulação;
c. o tipo de máquina;
d. a potência hidráulica (N) e a potência da máquina (Nm) sabendo que
seu rendimento é 72%.
Vamos lembrar que para
aplicarmos a equação da energia,
nós temos que conhecer o sentido
do escoamento e para isto
consideramos que em um trecho
sem máquina o fluido escoa da
maior carga para a menor carga.
a )  PHR no eixo do tubo resulta :
p 2 v 22
v 22
H2  z2 

 0  3,6 
g
2g
19,6
p3 v32
v32
0,24  10 4  9,8 v32
H3  z3 

0

 2,4 
g 2g
9800
19,6
19,6
Como a área do tubo é constante, temos que v 2  v3  H 2  H 3 ,
o que implica que o fluido escoa de (2) para (3), ou seja, de (1) para (5)
p1 v12
p 2 v 22
H1  H 2  H p
 z1 

 z2 

 Hp
1 2
1 2
g 2g
g
2g
v 22
4  0  0 )  3,6 
 0  v2 
19,6
  0,12
m3
Q  2,8 
 0,02199
4
s
4  3,6  19,6  2,8 m
s
b)  H p
tubulação
 Hp
1 2 
Hp
2 3 
Hp
3 4 
Hp
4 5
Nota : 3 - 4 são respectivamente entrada e saída da máquina e neste caso a perda é
considerada no rendimento da máquina
 Hp
 Hp
 H 2  H 3  3,6  2,4  1,2m
tubulação
2 3
c)  H1  H M  H 5  H p
tubulação
 4  H M  1,2  1,2
 H M  2,4  4  1,6m  0  é turbina hidráulica
d)  N  g  Q  H M  9800  0,02199  1,6  344,8W
O cálculo de NB fica
para a próxima aula