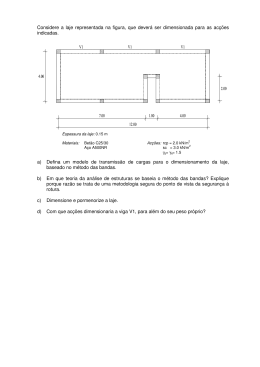
Trabalho de Análise de Estruturas II
Licenciatura Bi-etápica em Engenharia Civil
Responsável: Prof. Vitor Leitão
1º Semestre
Ano lectivo 2003-2004
Observações:
Trabalho individual ou grupos de dois elementos.
Pode optar entre analisar uma placa ou uma laje.
Entregar até à data do 2º exame.
Qualquer programa de elementos finitos pode ser usado. Referir qual a versão do
programa utilizado.
Análise de uma placa com um programa de elementos finitos:
Considere a placa em estado plano de tensão representada na figura:
E=210x106 kN/m2
espessura=0,02m
ν=0,3
peso específico=77 kN/m3
L1 = 3
ux
L2 =6
tx
uy
ty
A
B
C
D
E
F
1. Defina, de acordo com a tabela, as condições de fronteira da placa;
2. Defina um modelo com entre 20 a 40 elementos finitos (triangulares de 3 nós ou
quadrangulares de 4 nós):
a. Corra o programa e analise a solução obtida: mostre, nomeadamente, que a
solução obtida não satisfaz as condições de fronteira estáticas mas satisfaz o
equilíbrio global.
b. Escolha pelo menos duas grandezas que julge mais relevantes (uma
componente de tensão e/ou um deslocamento num ponto mais crítico) para
avaliar a qualidade da solução e registe esses valores;
3. Refine a malha e corra de novo o programa. O refinamento pode ser conseguido
através do aumento do número de elementos (refinamento h) ou através da
consideração de elementos mais ricos (refinamento p) ou ambos.
a. Registe as mesmas grandezas que escolheu atrás e compare os resultados.
Trabalho de Análise de Estruturas II
Licenciatura Bi-etápica em Engenharia Civil
Responsável: Prof. Vitor Leitão
1º Semestre
Ano lectivo 2003-2004
Observações:
Trabalho individual ou em grupos de dois elementos.
Pode optar entre analisar uma placa ou uma laje.
Entregar até à data do 2º exame.
Qualquer programa de elementos finitos pode ser usado. Referir qual a versão do
programa utilizado.
Análise de uma laje com um programa de elementos finitos:
Considere a laje representada na figura.
L1 =6
L2 =3
espessura=0,20 m
E=30x106 kN/m2
ν=0,15
q= 5 kN/m2
Simp ap
Encastr.
Livre
A
B
C
D
E
F
1. Defina as condições de fronteira da laje;
2. Defina um modelo com entre 20 a 40 elementos finitos (triangulares de 3 nós ou
quadrangulares de 4 nós):
a. Corra o programa e analise a solução obtida: mostre, nomeadamente, que a
solução obtida não satisfaz as condições de fronteira estáticas mas satisfaz o
equilíbrio global;
b. Escolha pelo menos duas grandezas que julge mais relevantes (um esforço e/ou
um deslocamento num ponto mais crítico) para avaliar a qualidade da solução e
registe esses valores;
3. Refine a malha e corra de novo o programa. O refinamento pode ser conseguido
através do aumento do número de elementos (refinamento h) ou através da
consideração de elementos mais ricos (refinamento p) ou ambos.
a. Registe as mesmas grandezas que escolheu atrás e compare os resultados.