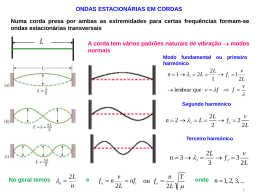
Patrocínio:
FINEP
PROJETO CIÊNCIA NA BAGAGEM
Roteiro para estudo de vídeo
Prof.:
Curso:
Data: _____/_____/_____
Aluno:
Sala :
n°:
Turma:
Aluno:
n°:
Roteiro elaborado por Luiz André Mützenberg para o filme vt_cb_16.mpg - Projeto Ciência na Bagagem - http://gaia.liberato.com.br/ciencianabagagem
ONDAS ESTACIONÁRIAS
Objetivo: explicar a formação de ondas estacionárias em cordas.
As ondas estacionárias podem se formar quando dois
trens de onda idênticos se propagam em sentidos opostos no
mesmo espaço. É fácil obter dois trens de onda idênticos que
se propagam em sentidos opostos, basta fixar a extremidade
de uma corda e oscilar a outra extremidade. Quando a perturbação provocada numa extremidade atinge a extremidade
fixa a onda é refletida e interfere com a onda que ainda não
foi refletida, mas a onda estacionária só se forma se forem
satisfeitas as condições de ressonância. A Fig. 1 mostra algumas ondas estacionárias geradas em uma corda com uma
extremidade fixa e outra perturbada pela rotação de um motor.
primentos de onda (). Matematicamente podemos escrever
que se formam ondas estacionarias se
4.L
Eq. 2

; n  1, 3, 5,
n
1. A corda utilizada nas filmagens possui um comprimento de
95 cm. Use esta informação e calcule  para as cinco ondas
estacionárias que aparecem na Fig. 1.
A tensão da corda não foi alterada durante as filmagens,
as diferentes condições de ressonância que aparecem na
Fig. 1 foram obtidas alterando a freqüência de rotação do
motor.
2. Para qual das ondas estacionárias que aparecem na Fig. 1
foi usada a maior freqüência? Justifique a resposta.
3. Qual a razão entre a maior e a menor freqüência usada
para gerar as ondas estacionárias da Fig. 1? Explique.
4. Considerando que a corda tem 95 cm determine a razão
entre v/f (velocidade de propagação / freqüência) para as
ondas estacionárias da Fig. 1. Considere unidades do SI.
Para Compreender o movimento da corda ao formar
uma onda estacionária foram tomados 5 instantâneos de uma
simulação feita no Modellus para uma onda com freqüência
de 4 Hz que se propaga com velocidade de 60 un/s em um
meio com 60 unidade de comprimento. Os instantâneos foram tomados em intervalos 0,025s.
nó
ventre
nó
ventre
nó
Fig. 1. Ondas estacionárias em uma corda.
As condições de ressonância dependem da forma de fixação o sistema vibrante. Quando a fixação impede a vibração da extremidade, diz-se que a extremidade é fixa. Quando
a extremidade pode vibrar livremente diz-se que a extremidade é livre. Uma corda de violão é um sistema com duas
extremidades fixas. Uma barra metálica deve ser fixa pelo
centro para que ressoe mais, este é um sistema com duas
extremidades livres. Um tubo sonoro pode ter uma extremidade aberta e outra fechada, na extremidade aberta as moléculas vibram livremente, na extremidade fichada as moléculas não vibram, portanto este é um sistema com uma extremidade fixa e outra livre.
Neste roteiro vamos limitar a analise a meios unidimensionais.
Quando ambas as extremidades são fixas, ou ambas são
livres, as ondas estacionárias se formam quando o comprimento do meio (L) corresponde a um número inteiro (n) de
meios comprimentos de onda (). Matematicamente podemos
escrever que se formam ondas estacionarias se:
2.L
Eq. 1

; n  1, 2, 3,
n
Quando uma extremidade é fixa e a outra é livre, as ondas estacionárias se formam quando o comprimento do meio
(L) corresponde a um número impar (n) de quartos de com-
Fig. 2. Cinco instantâneos das posições de diversos pontos de
um meio em que se forma uma onda estacionária e o resultado da
sobreposição destes instantâneos.
Os pontos da extremidade e do centro permanecem em
repouso, nestes pontos, chamados de nós, as ondas que se
propagam em sentido opostos interferem negativamente. Os
ventres são regiões em que ocorre interferência construtiva
fazendo a corda vibrar intensamente.
Referências
GASPAR, Alberto. Física 2-Ondas, ótica, termodinâmica. 1ª ed. São Paulo:
Ática. 2000
Conclusão: ___________________________________________________________________________________________