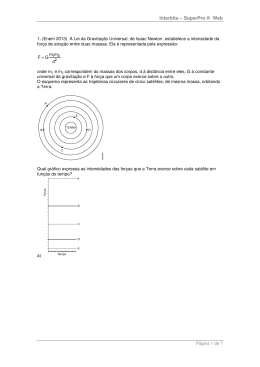
FÍSICA-Tomás
Gravitação Universal
Um pouco de História:
A gravitação universal tem haver com os corpos do Sistema
Solar.Durante séculos,houve muitas teorias sobre o Sol,os planetas e
como funcionava a mecânica do universo.
Aristóteles
Platão e Aristóteles consideravam que a Terra ocupava o centro do
Universo,e que os demais planetas giravam em torno dela
(Teoria Geocêntrica).
Platão
Segundo Copérnico,o Sol era o centro do Universo e os demais
planetas,incluindo a Terra,giravam em torno dele em órbitas circulares
(Teoria Heliocêntrica).
Embora tenha inventado o telescópio para melhor observar os
astros e proporcionar descobertas fantásticas que,comprovam a teoria
de Copérnico ,Galileu Galilei foi considerado louco,também foi
aprisionado e morto pela Inquisição.
Copérnico
Galileu
FÍSICA-Tomás
Gravitação Universal
As Leis de Kepler
1ª Lei de Kepler: Lei das órbitas
“Todos os planetas giram em torno do sol em
órbitas elípticas com o sol ocupando um dos
focos.”
Psiu!!
 Vale lembrar que,teoricamente a órbita de um
planeta,em torno de uma estrela,pode ser
circular;apenas a órbita elíptica é mais provável.
FÍSICA-Tomás
Gravitação Universal
2ª Lei de Kepler: Lei das áreas
“Um planeta,em sua órbita em torno do sol,varre
áreas iguais em intervalos de tempo iguais.”
S2
S1
Como
S 1
t

S2
 V1  V2
t
À medida em que o planeta aproxima-se do sol sua
velocidade aumenta.
FÍSICA-Tomás
Gravitação Universal
FÍSICA-Tomás
Gravitação Universal
Psiu!!
A velocidade areolar (razão entre a área varrida pelo
raio vetor e o intervalo de tempo gasto) de cada planeta
é constante.
Vareolar
Area

t
FÍSICA-Tomás
Gravitação Universal
3ª Lei de Kepler: Lei dos períodos
“O quadrado do período de translação de
um planeta em torno do sol é proporcional
ao cubo do raio médio de sua órbita.”
T2
 CONSTANTE
3
R
FÍSICA-Tomás
Gravitação Universal
FÍSICA-Tomás
Gravitação Universal
FÍSICA-Tomás
Gravitação Universal
FÍSICA-Tomás
Gravitação Universal
Observe que,sendo G uma constante
universal,a velocidade de translação tem
módulo dependente apenas da massa do
planeta e do raio de sua órbita.
Para o mesmo planeta,quanto mais próximo for o satélite,maior sua
velocidade de translação.
Período de translação(T)
Sendo
R3
T  2
GM
,vem:
4 2 R3
T
GM
Observe que o período de um satélite só depende
da massa do planeta e do raio de sua órbita.
FÍSICA-Tomás
Gravitação Universal
FÍSICA-Tomás
Gravitação Universal
Satélite estacionário
 Um satélite é dito “estacionário”
quando ocupa sempre a mesma posição
em relação a um referencial ligado à
superfície do planeta.
Para que um satélite seja
estacionário,ele deve satisfazer as
condições seguintes:
a) Plano de órbita: a órbita deve estar
contida no plano equatorial do planeta.
b) Trajetória: a órbita deve ser circular.
c) Período de translação: igual ao período
de rotação do planeta.
FÍSICA-Tomás
Gravitação Universal
Em se tratando de um satélite estacionário da terra,o
período de translação deve ser de 24h e o raio da
órbita,calculado pela 3ª Lei de Kepler,corresponde
a,aproximadamente,6,7 raios terrestres.
O satélite estacionário tem aplicação em
telecomunicações.
FÍSICA-Tomás
Gravitação Universal
Considere um corpo de massa m,animado de velocidade v,a uma distância R
do centro de um planeta de massa M.
mv 2
Ec 
2
v2 
GM
R
Ec 
m GM
.
2 R
Ec 
GMm
2R
Considerando nula a energia potencial do campo quando a distância d
entre os corpos tende para o infinito(Epot=0),pode-se demonstrar,com
auxílio de cálculo integral,que a energia potencial,associada ao campo
de forças será dado por: Epot   GMm
R
O fato da energia potencial ser negativa quer dizer apenas que:
Em todos os pontos do campo a energia potencial é menor do que no infinito.
FÍSICA-Tomás
Gravitação Universal
Em  Ec  Ep
GMm GMm
Em 

2R
R
GMm
Em  
2R
FÍSICA-Tomás
Gravitação Universal
VELOCIDADE DE ESCAPE
Velocidade mínima com que um corpo deve ser lançado para
escapar do campo gravitacional de um planeta ou corpo
celeste.
Para a terra VEsc 11,2Km/s=11.200m/s
VEsc
2GM

R
Como: g 0 
GM
2

GM

g
.R
0
R2
Logo:
VEsc 
FÍSICA-Tomás
2 g0 . R 2

R
VEsc  2 g0 .R
Gravitação Universal
01.(UEFS-08.1) Um satélite descreve movimento uniforme
em torno da Terra em uma órbita circular de raio igual a
1,0.107m.
Desprezando-se outras forças sobre o satélite, que não
seja a gravitacional da Terra, pode-se concluir que a razão
entre a energia cinética do satélite e o módulo da
resultante centrípeta no satélite é, aproximadamente,
igual, em 106J/N, a
a) 2
b) 3
c) 4
d) 5
e) 6
FÍSICA-Tomás
Gravitação Universal
02)(UESB-08) Sabendo-se que a massa e o raio médio da
Terra são, respectivamente, iguais a 5,98.1024kg e
6,37.106m, a constante de gravitação universal, G = 6,67.
10-11Nm2/kg2, e desprezando-se os efeitos da resistência
do ar, a menor velocidade à que se deve lançar um corpo
da superfície da terrestre para que esse escape da
atração da Terra, em m/s, é da ordem de
01) 102
02) 103
03) 104
FÍSICA-Tomás
04) 105
05) 106
Gravitação Universal
03.(UESC-08)Considere um satélite geoestacionário,
com massa igual a 5,0kg, descrevendo um movimento
uniforme em uma órbita circular de raio igual a 7,0.
1 03km em torno da Terra.
Sabendo-se que a massa da Terra é igual a
5,98.1024Kg e a constante da Gravitação Universal é
igual a 6,67.10-11Nm2/kg2, pode-se afirmar que a ordem
de grandeza do módulo da quantidade de movimento
desse satélite é igual, em kg.mls, a
01) 108
02) 107
03) 106
04) 105
05) 104
FÍSICA-Tomás
Gravitação Universal
04.(UESB-09.2)Considere dois astronautas de massas
iguais a 50,0kg e 60,0kg,separados por uma distância
de 5,0m e soltos no espaço,longe da influência de
outros corpos.
Sabendo-se que a constante de gravitação
universal é igual a 6,7.10-11kgm2kg-2,a ordem de
grandeza do módulo da força que farão com que eles
se aproximem,no SI,é igual a
a) 10-5
b) 10-8
c) 10-9
d) 10-10
e) 10-13
FÍSICA-Tomás
Gravitação Universal