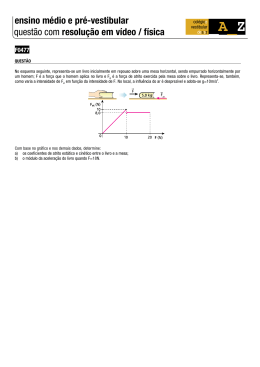
Trabalho Máximo
Para mostrar que é máxima a quantidade de energia trocada entre o sistema e
a vizinhança por trabalho quando o processo é reversível, vamos considerar uma
amostra de gás dentro de um cilindro fechado por um pistão móvel e sem atrito, sobre
o qual repousa um corpo A, de massa m. A amostra de gás está isolada termicamente
e em equilíbrio. A amostra de gás representa o sistema e o corpo A, a vizinhança.
Para descobrir qual o processo (adiabático) em que a quantidade de energia
associada ao trabalho realizado pela amostra de gás sobre o corpo A é máxima, como
primeira tentativa deslocamos o corpo A horizontalmente (Fig.56).
Com isso, o pistão dispara para cima e, depois de algumas oscilações, atinge o
estado de equilíbrio a certa altura h. Como o corpo A não é deslocado verticalmente, a
amostra de gás não realiza trabalho sobre ele. A quantidade de energia associada ao
trabalho realizado pela amostra de gás sobre o corpo é nula.
Como segunda tentativa, dividimos o corpo A em duas partes iguais e
deslocamos uma delas horizontalmente (Fig.57).
Com isso, o pistão dispara para cima e alcança o equilíbrio a uma altura ½ h.
Então, deslocamos horizontalmente a outra parte do corpo A e, com isso, o pistão
alcança a posição de equilíbrio final elevando-se mais ½ h. Nesta tentativa, a amostra
de gás realiza trabalho sobre a metade do corpo A, elevando-a a uma altura ½ h. A
quantidade de energia associada ao trabalho da amostra de gás sobre o corpo é:
m h  1
W =   g   =   mgh
 2  2 4
Grupo de Ensino de Física da Universidade Federal de Santa Maria
Como terceira tentativa, dividimos o corpo A em três partes iguais e repetimos
o procedimento feito na segunda tentativa, deslocando horizontalmente uma parte de
cada vez. Assim, a quantidade de energia associada ao trabalho realizado pela
amostra de gás sobre o corpo A é:
 2m   h   m   h   1 
W =
 g   +   g   =   mgh
 3  3  3  3 3
A partir dos resultados destas tentativas, podemos concluir que a quantidade
de energia associada ao trabalho realizado pela amostra de gás sobre o corpo A é
máxima quando o corpo A é dividido no maior número possível de partes e estas são,
uma a uma, deslocadas horizontalmente. Cada vez que uma dessas partes é movida
horizontalmente, a amostra de gás tem uma pequena mudança porque o pistão sobe
uma pequena fração da altura h. A última parte do corpo A é deslocada
horizontalmente com o pistão quase na altura h. Não é difícil ver que, no final das
contas, a quantidade de energia associada ao trabalho realizado pela amostra de gás
sobre o corpo A é equivalente à quantidade de energia necessária para elevar o corpo
até uma altura h/2. Então:
 1
W = WMAX =   mgh
2
O processo desenvolvido em passos infinitesimais e sem atrito é aquele para o
qual a quantidade de energia associada ao trabalho realizado pela amostra de gás
sobre o corpo A é máxima. O processo desenvolvido em passos infinitesimais é
quase-estático e porque não existe atrito, é reversível.
Grupo de Ensino de Física da Universidade Federal de Santa Maria