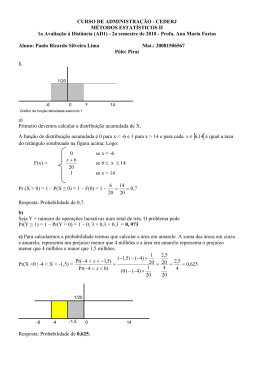
CURSO DE ADMINISTRAÇÃO - CEDERJ
MÉTODOS ESTATÍSTICOS II
1a Avaliação à Distância (AD1) - 2o semestre de 2011 - Profa. Ana Maria Farias
1. Quando o Departmento de Transportes (DOT) repinta as faixas centrais, laterais ou de zonas
de não ultrapassagem em uma rodovia, a tinta epóxi é usada algumas vezes. Essa tinta é
mais cara do que o látex, mas dura mais. Se essa tinta espirra em um veículo, ela tem que
ser completamente removida, e a área do carro atingida tem que ser repintada. O DOT avisa
aos motoristas que o tempo de secagem dessa tinta epóxi (em minutos) tem uma distribuição
uniforme no intervalo (30, 60). Suponha que a tinta epóxi seja aplicada a uma pequena seção
de faixa central.
(a) Qual é a probabilidade de que a tinta seque entre 40 e 50 minutos?
Solução
Seja T = tempo de secagem da tinta. Então, T ∼ U nif (30; 60)
Pr(40 < T < 50) =
1
50 − 40
=
60 − 30
3
(b) Ache um valor t tal que a probabilidade de a tinta levar, pelo menos, t minutos para secar
seja 0,75.
Solução
Pr(T ≥ t) = 0, 75 ⇐⇒
t − 30
= 0, 75 ⇐⇒ t = 30 + 30 × 0.75 ⇐⇒ t = 52, 5 min
60 − 30
(c) Se a equipe de estradas do DOT remove todos os cones da faixa central 55 minutos depois
da pintura, qual é a probabilidade de que a tinta ainda esteja molhada nesse instante?
Solução
1
60 − 55
=
Pr(T > 55) =
60 − 30
6
2. Na figura 1 é dado o gráfico da função de densidade f de uma variável aleatória contínua X.
Figura 1: Função de densidade para a questão 2
1
(a) Determine o valor de k e a expressão matemática de f.
Solução
Temos que ter
k≥0
É usual o aluno esquecer de verificar a condição de não negatividade! Chame atenção
para esse fato.
A área tem que ser 1:
1
· 20 · k = 1 ⇒ k = 0, 1
2
Como f (x) é linear e passa pelo ponto (0, k), resulta que f (x) = ax + k = ax + 0, 1. f (x)
também passa passa pelos pontos (20; 0), o que nos dá:
20a + 0, 1 = 0 =⇒ a = −0, 005
Logo,
fX (x) =
½
−0, 005x + 0, 1
0
se 0 ≤ x ≤ 20
se x < 0 ou x > 20
(b) Determine a função de distribuição acumulada FX de X.
Solução
Para x < 0, FX (x) = 0 e para x > 20, FX (x) = 1. Para 0 ≤ x ≤ 20, FX (x) é a
área do trapézio sombreada na Figura 2. Esse trapézio tem altura x,base menor igual a
fX (x) = −0, 005x + 0, 1 e base maior igual a 0,1. Logo,
⎧
0
⎪
⎨
(−0, 005x + 0, 1 + 0, 1) · x
FX (x) =
= 0, 1x − 0, 0025x2
⎪
2
⎩
1
se x < 0
se 0 ≤ x ≤ 20
se x > 20
Figura 2: Função de distribuição acumulada para a questão 2b
(c) Determine os quartis da distribuição variável aleatória X.
Solução
2
Sejam Q1 , Q2 , Q3 os quartis. Então, temos que ter
FX (Q1 ) = 0, 25 =⇒ 0, 1Q1 − 0, 0025Q21 = 0, 25 =⇒ Q21 − 40Q1 + 100 = 0 =⇒
√
√
√
40 ± 400 × 3
40 ± 20 3
40 ± 1600 − 400
=
=
Q1 =
2
2
2
FX (Q2 ) = 0, 5 =⇒ 0, 1Q2 − 0, 0025Q22 = 0, 5 =⇒ Q22 − 40Q2 + 200 = 0 =⇒
√
√
√
40 ± 400 × 2
40 ± 20 2
40 ± 1600 − 800
=
=
Q2 =
2
2
2
FX (Q3 ) = 0, 75 =⇒ 0, 1Q3 − 0, 0025Q23 = 0, 25 =⇒ Q23 − 40Q3 + 300 = 0 =⇒
√
√
40 ± 400
40 ± 20
40 ± 1600 − 1200
=
=
Q3 =
2
2
2
As soluções dentro do domínio de definição de f são
√
√
40 − 20 3
40 − 20 2
Q1 =
= 2, 6795
Q2 =
= 5, 8579
2
2
Q3 =
40 − 20
= 10
2
A solução a seguir envolve apenas a função de densidade, ou seja, calculamos a probabilidade como área sob a curva da função de densidade. É importante chamar atenção para a
diferença entre as duas. Em geral, os alunos calculam probabilidades do tipo Pr(X ≤ x)
calculando f (x),e não F (x). Em termos da função de densidade temos o seguinte: a área
à esquerda de Q1 é 0, 25, de Q2 é 0, 50 e de Q3 é 0, 75. Pela Figura 2, cada uma dessas
áreas é a área de um trapézio:
Q1
Q2
Q3
(−0, 005 · Q1 + 0, 1 + 0, 1) · Q1
= 0, 25 ⇒ −0, 005Q21 + 0, 2Q1 − 0, 50 = 0
2
⇒ Q21 − 40Q1 + 100 = 0
(−0, 005 · Q2 + 0, 1 + 0, 1) · Q2
= 0, 50 ⇒ −0, 005Q22 + 0, 2Q2 − 1 = 0
:
2
⇒ Q22 − 40Q2 + 200 = 0
(−0, 005 · Q3 + 0, 1 + 0, 1) · Q3
= 0, 75 ⇒ −0, 005Q23 + 0, 2Q3 − 1, 5 = 0
:
2
⇒ Q23 − 40Q2 + 300 = 0
:
Essas são as mesmas equações obtidas anteriormente.
3. Seja X ∼ N (28; 72 ). Calcule:
(a) Pr(X ≥ 36, 4)
Solução
Veja a Figura 3.
¶
µ
36.4 − 28
= Pr(Z ≥ 1, 2) = 0, 5 − Pr(0 ≤ Z ≤ 1, 2)
Pr(X ≥ 36, 4) = Pr Z ≥
7
= 0, 5 − tab(1, 2) = 0, 5 − 0, 38493 = 0, 11507
3
Figura 3: Solução da questão 3(a)
(b) Pr(X < 14)
Solução
Veja a Figura 4.
¶
µ
14 − 28
= Pr(Z < −2) = Pr(Z > 2) = 0, 5 − Pr(0 ≤ Z ≤ 2) =
Pr(X < 14) = Pr Z <
7
= 0, 5 − tab(2) = 0, 5 − 0, 47725 = 0, 02275
Figura 4: Solução da questão 3(b)
(c) Pr(16, 8 < X < 30, 8)
Solução
Veja a Figura 5.
µ
¶
16.8 − 28
30.8 − 28
Pr(16, 8 < X < 30, 8) = Pr
<Z<
= Pr(−1, 6 < Z < 0, 4) =
7
7
= Pr(−1, 6 < Z < 0) + Pr(0 ≤ Z ≤ 0, 4) =
= Pr(0 < Z < 1, 6) + Pr(0 ≤ Z ≤ 0, 4) = tab(1, 6) + tab(0, 4) =
= 0, 44520 + 0, 15542 = 0, 60062
(d) Pr(26, 4 < X < 33, 6)
4
Figura 5: Solução da questão 3(c)
Solução
Veja a Figura 6.
µ
¶
26.4 − 28
33.6 − 28
Pr(26, 4 < X < 33, 6) = Pr
<Z<
= Pr(−0, 23 < Z < 0, 8) =
7
7
= tab(0, 8) − tab(0, 23) = 0.091 + 0.2881 = 0, 3791
Figura 6: Solução da questão 3(d)
(e) Pr[(X > 23, 8) ∪ (X < 33, 6)]
Solução
Note que temos a probabilidade da união de 2 eventos: A = (X > 23, 8) e B = (X <
33, 6). Sabemos que Pr(A∪B) = Pr(A)+Pr(B)−Pr(A∩B). Vamos calcular cada parcela.
Na parte esquerda da Figura 7 ilustra-se o cálculo de Pr(X > 23, 8) e na parte direita, o
cálculo de Pr(X < 33, 6).Em ambas as figuras, a parte listada refere-se à probabilidade
da interseção, contada 2 vezes.
¶
µ
23.8 − 28
= Pr(Z > −0, 6) = 0, 5 + tab(0, 6) =
Pr(X > 23, 8) = Pr Z >
7
= 0, 5 + 0, 22575 = 0, 72575
5
Figura 7: Solução da questão 3(e)
¶
µ
33.6 − 28
= Pr(Z < 0, 8) = 0, 5 + tab(0, 8)
Pr(X < 33, 6) = Pr Z <
7
= 0, 5 + 0, 28814 = 0, 78814
µ
23.8 − 28
33.6 − 28
Pr(23, 8 < X < 33, 6) = Pr
<Z<
7
7
Pr(−0, 6 < Z < 0, 8) = tab(0, 8) + tab(0, 6)
¶
=
= 0.28814 + 0.22575 = 0, 51389
Pr[(X > 23, 8) ∪ (X < 33, 6)] = 0.72575 + 0.78814 − 0.51389 = 1
Comente porque esse resultado já era esperado! Observe que a união das áreas sombreadas
dá o espaço amostral completo!
4. Seja X ∼ N (μ; σ 2 ).
(a) Calcule Pr(|X − μ| > kσ) para k = 1, 2, 3.
Solução
Pr(|X − μ| > 1σ) = Pr(X − μ < −σ) + Pr(X − μ > σ)
¶
µ
¶
µ
X −μ
X −μ
< −1 + Pr
> 1 = Pr(Z < −1) + Pr(Z > 1)
= Pr
σ
σ
= 2 × Pr (Z > 1) = 2 × [0, 5 − Pr (0 ≤ Z ≤ 1)]
= 2 × [0, 5 − tab(1, 0] = 2 × (0, 5 − 0.34134) = 0, 31732 ≈ 0, 32
Pr(|X − μ| > 2σ) = Pr(X − μ < −2σ) + Pr(X − μ > 2σ)
¶
µ
¶
µ
X −μ
X −μ
< −2 + Pr
>2
= Pr
σ
σ
= Pr(Z < −2) + Pr(Z > 2) = 2 × Pr (Z > 2) = 2 × [0, 5 − Pr (0 ≤ Z ≤ 2)]
= 2 × [0, 5 − tab(2, 0] = 2 × (0, 5 − 0.47725) = 0, 0455 ≈ 0, 05
6
Pr(|X − μ| > 3σ) = Pr(X − μ < −3σ) + Pr(X − μ > 3σ)
µ
¶
µ
¶
X −μ
X −μ
= Pr
< −3 + Pr
>3
σ
σ
= Pr(Z < −3) + Pr(Z > 3) = 2 × Pr (Z > 3) = 2 × [0, 5 − Pr (0 ≤ Z ≤ 3)]
= 2 × [0, 5 − tab(3, 0] = 2 × (0, 5 − 0.49865) = 0, 0027 ≈ 0, 003
(b) Calcule o valor de k tal que Pr(|X − μ| < kσ) = 0, 95
Solução
Pr(|X − μ| < kσ) = 0, 95 ⇐⇒ Pr(−kσ < X − μ < −kσ) = 0, 95 ⇐⇒
¶
µ
X −μ
< k = 0, 95 ⇐⇒ Pr (−k < Z < k) = 0, 95 ⇐⇒
Pr −k <
σ
2 × Pr (0 < Z < k) = 0, 95 ⇐⇒ Pr (0 < Z < k) = 0, 475 ⇐⇒
tab (k) = 0, 475 ⇐⇒ Φ(k) = 0, 975 ⇐⇒ k = 1, 96
(c) Calcule o valor de k tal que Pr(X − μ > kσ) = 0, 05
Solução
Pr(X − μ > kσ) = 0, 05 ⇐⇒ Pr (Z > k) = 0, 05
Note que k tem que ser positivo, pois à direita dele tem 5% de área e à esquerda, 95%.
Assim, k tem que estar do lado positivo do eixo!
Pr (Z > k) = 0, 05 ⇐⇒ 0, 5 − Pr(0 ≤ Z ≤ k) = 0, 05 ⇐⇒
0, 5 − tab(k) = 0, 05 ⇐⇒ tab(k) = 0, 45 ⇐⇒ k = 1, 64
(d) Calcule o valor de k tal que Pr(X − μ < kσ) = 0, 10
Solução
Pr(X − μ < kσ) = 0, 10 ⇐⇒ Pr(Z < k) = 0, 10
Note que k tem que ser negativo, pois à esquerda dele tem 10% de área e à direita, 90%.
Assim, k tem que estar do lado negativo do eixo e seu simétrico −k tem que estar do
lado positivo!
Pr(Z < k) = 0, 10 ⇐⇒ Pr(Z > −k) = 0, 10 ⇐⇒ 0, 5 − Pr(0 ≤ Z ≤ −k) = 0, 10 ⇐⇒
0, 5 − tab(−k) = 0, 10 ⇐⇒ tab(−k) = 0, 40 ⇐⇒ −k = 1, 28 ⇐⇒ k = −1, 28
(e) Interprete os resultados obtidos.
Solução
O importante a notar neste exercício é que os resultados valem para qualquer distribuição
normal. Por exemplo, do item (a), resulta que, para qualquer distribuição normal,
o intervalo [μ − σ; μ + σ] tem 68% de probabilidade
o intervalo [μ − 2σ; μ + 2σ] tem 95% de probabilidade
o intervalo [μ − 3σ; μ + 3σ] tem 99,7% de probabilidade
Veja a Figura 8 Assim, o desvio padrão funciona como uma medida de escala, ou seja,
podemos falar em termos de número de desvios padrões. Por exemplo, do item (c),
conclui-se que acima de 1,64 desvios padrões da média temos sempre 5% de probabilidade
7
Figura 8: Solução da questão 4(e)
8
5. As baterias AAA, usadas em muitas calculadoras, são fabricadas de acordo com especificações
que regulam o diâmetro, a altura, a capacidade avaliada, o peso e o volume. O volume de uma
bateria AAA selecionada alea
(a) Ache um valor v tal que apenas 10% de todas as baterias tenham volume inferior a v.
Solução
A área à esquerda de v é 10%. Logo, v tem que ser menor que a média, ou seja, a abscissa
da normal padronizada tem que ser negativa!
¶
µ
¶
µ
v − 3, 85
v − 3, 85
= 0, 10 ⇐⇒ Pr Z > −
= 0, 10
Pr(V
< v) = 0, 10 ⇐⇒ Pr Z <
0, 01
0, 01
µ
¶
3, 85 − v
3, 85 − v
⇐⇒ tab
= 0, 40 ⇐⇒
= 1, 28 ⇐⇒ v = 3, 8372
0, 01
0, 01
(b) Se uma bateria tem volume 3,88 cm3 ou mais, ela não se encaixará perfeitamente dentro da
canaleta. Para uma calculadora que requer quatro baterias AAA, qual é a probabilidade
de que todas as quatro baterias não se encaixem?
Solução
A probabilidade de uma bateria não se encaixar é
¶
µ
3, 88 − 3, 85
= Pr(Z ≥ 3) = 0, 5−tab(3) = 0.5−0.4987 = 0, 0013
Pr(V ≥ 3, 88) = Pr Z ≥
0, 01
Supondo independência (razoável, nesse caso), a probabilidade de as 4 baterias não se
encaixarem será
p = 0.0013 × 0.0013 × 0.0013 × 0.0013 ≈ 0
6. Dióxido de carbono pressurizado é, em geral, adicionado à soda para amenizar o gosto doce
da bebida e impedir o crescimento de alguns micróbios. Embora a quantidade de dióxido de
carbono varie, a maioria das sodas é engarrafada sob alta pressão. A pressão interna de uma
lata refrigerada de certo refrigerante tem um valor médio de 276 quilopascals (kPa) a 16◦ C.
Suponha que a pressão seja normalmente distribuída, com desvio padrão de 7 kPa. Uma lata
desse refrigerante (a 16◦ C) é selecionada aleatoriamente.
(a) Se a pressão interna for superior a 300 kPa, ao se abrir a lata, o líquido derramará para
fora. Qual é a probabilidade de que haja um derramamento?
Solução
¶
µ
300 − 276
= Pr(Z > 3, 43) = 0, 5−tab(3, 43) = 0.5−0.4997 = 0, 0003
Pr(X > 300) = Pr Z >
7
(b) Se uma pessoa sacode a lata por um mínimo de 30 segundos a pressão interna média muda
para 289 kPa (enquanto o desvio padrão permanece o mesmo). Qual é a probabilidade
de que o líquido em uma lata que foi sacudida derrame para fora da lata quando esta for
aberta?
Solução
Seja Y a variável aleatória que descreve a pressão interna da lata após ser sacudida.
Então, Y ∼ N (289; 72 )
¶
µ
300 − 289
= Pr(Z > 1, 57) = 0, 5−tab(1, 57) = 0.5−0.4418 = 0, 0582
Pr(Y > 300) = Pr Z >
7
9