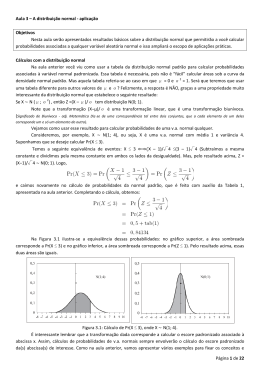
CURSO DE ADMINISTRAÇÃO - CEDERJ
MÉTODOS ESTATÍSTICOS II
1a Avaliação à Distância (AD1) - 2o semestre de 2010 - Profa. Ana Maria Farias
Aluno: Paulo Ricardo Silveira Lima
Mat.: 20081506567
Pólo: Piraí
1.
1/20
-6
x
0
14
Gráfico da função densidade exercício 1
a)
Primeiro devemos calcular a distribuição acumulada de X.
A função de distribuição acumulada é 0 para x < -6 e 1 para x > 14 e para cada x ∈ ]6,14[ é igual a área
do retângulo sombreado na figura acima; Logo:
0
x+6
20
1
F(x) =
se x < -6
se 6 ≤ x ≤ 14
se x > 14
Pr (X > 0) = 1 – P(X ≤ 0) = 1 – F(0) = 1 -
6 14
=
= 0,7
20 20
Resposta: Probabilidade de 0,7.
b)
Seja Y = número de operações lucrativas num total de três. O problema pede
Pr(Y ≥ 1) = 1 − Pr(Y = 0) = 1 − 0, 3 × 0,3 × 0,3 = 0, 973
c) Para calcularmos a probabilidade termos que calcular a área em amarelo. A soma das áreas em cinza
e amarelo, representa um prejuízo menor que 4 milhões e a área em amarelo representa o prejuízo
menor que 4 milhões e maior que 1,5 milhões.
1
2,5
(−1,5) − (−4) ×
Pr(−4 < x < −1,5)
20 = 20 = 2,5 = 0,625
Pr(X <0 | -4 < X < -1,5) =
=
1
4
Pr(−4 < x < 0)
4
(0) − (−4) ×
20
20
1/20
-6
-4
-1,5
0
Resposta: Probabilidade de 0,625.
14
2)
a.1) Para encontrarmos K, a área do triângulo sob a reta tem que ser igual a 1, então teremos:
k 1
k
3 ± 9 + 4 × 18
1 = (3k − 3) × × ⇒ 1 = (3k − 3) × ⇒ 3k 2 − 3k − 6 ⇒ k =
3 2
6
6
A raiz que fornece resultado dentro do domínio de variação é:
3 + 81 12
=
=2
6
6
Resposta: K=2
k=
a.2) Como F(x) é uma linear e a reta passa pelos pontos (3;0) e (6; 2/3) teremos o seguinte sistema de
equações:
0 = a + 3b
2
= a + 6b
3
Subtraindo as equações teremos:
2
2
= 3b ⇒ b =
3
9
Substituindo b na primeira equação teremos: 0 = a + 3 ×
Resposta:
F(x) =
0
2 2
− + x
3 9
0
se x < 3
se 3 ≤ x ≤
se x >
2
3
2
3
2
2
⇒a=−
9
3
b) A função de distribuição acumulada é dada por: FX (x) = Pr (X ≤ x), então termos:
2
2
Essa área é a área de um triângulo com base (x − 3) e altura  x − 
3
9
2 1  x − 3  2
2  x2 2
2
F(x) = ( x − 3) ×  x −  × = 
×
x
−
− x +1
 
=
3 2  2  9
3 9 3
9
Resposta:
0
se x < 3
2
F(x) =
x
2
− x +1
9 3
1
se 3 ≤ x ≤ 6
se x > 6
x−3
= 0,5 ⇒ x = 4,5 , logo Q2 = 4,5
3
x−3
Para definirmos Q1 teremos F (Q1 ) = 0,25 , logo
= 0,25 ⇒ x = 3,75 , logo Q1 = 3,75
3
x −3
Para definirmos Q3 teremos F (Q3 ) = 0,75 , logo
= 0,75 ⇒ x = 5,25 , logo Q3 = 5,25
3
Respostas:
c) Para definirmos Q2 teremos F (Q2 ) = 0,5 , logo
Q1 = 3,75, Q2 = 4,5 e Q3 = 5,25
3) Seja X ~ N (27; 72). Calcule:
(a) Pr(X ≥ 35, 4):
Pr( X ≥ 35,4) =
35,4 − 27 

Pr Z ≥
 = Pr( Z ≥ 1,2) = 0,5 − Pr(0 ≤ Z ≤ 1,2) = 0,5 − tab(1,2) = 0,5 − 0,38493 = 0,11507
7


(b) Pr(X < 13):
13 − 27 

Pr( X < 13) = Pr Z <
 = Pr( Z < −2) = Pr( Z > 2) = 0,5 − Pr(0 ≤ Z ≤ 2) = 0,5 − tab(2) =
7 

= 0,5 − 0,47725 = 0,02275
(c) Pr(15, 8 < X < 29, 8)
 15,8 − 27 
 29,8 − 27 
Pr(15,8 < X < 29,8) = Pr
<Z <
 = Pr(−1,6 < Z < 0,4) =
7
7




= Pr(−1,6 < Z < 0) + Pr(0 ≤ Z ≤ 0,4) = Pr(0 < Z < 1,6) + Pr(0 ≤ Z ≤ 0,4) =
= tab(1,6) + tab(0,4) = 0,44520 + 0,15542 = 0,60062
(d) Pr(36, 8 < X < 45, 2) =
 36,8 − 27 
 45,2 − 27 
= Pr
<Z <
 = Pr(1,4 < Z < 2,6) = tab(2,6) − tab(1,4) = 0,49534 − 0,41924 = 0,0761
7
7




(e) Pr[(X > 22, 8) U (X < 32, 6)]
Neste caso temos a probabilidade da união de 2 eventos: A = (X > 22,8) e B = (X < 32,6). Sabemos que Pr(A U B) = Pr(A)
+ Pr(B) − Pr(A ∩ B). Então teremos que calcular cada parcela.
Para: Pr(X>22,8)
22,8 − 27 

Pr( X > 22,8) = Pr Z >
 = Pr( Z > −0,6) = 0,5 + tab(0,6) = 0,5 + 0,22575 = 0,72575
7


Para: Pr(X<32,6)
32,6 − 27 

Pr( X < 32,6) = Pr Z <
 = Pr( Z < 0,8) = 0,5 + tab(0,8) = 0,5 + 0,28814 = 0,78814
7


Para: Pr(22,8<X<32,6)
32,6 − 27 
 22,8 − 27
Pr(22,8 < x < 32,6) = Pr 
<Z<
 = Pr(−0,6 < Z < 0,8) = tab(0,8) + tab(0,6) =
7
7


= 0,28814 + 0,22575 = 0,51389
Então teremos:
Pr(22,8 < x < 32,6) = Pr( X > 22,8) + Pr( X < 32,6) − Pr(22,8 < X < 32,6)
= 0,72575 + 0,78814 − 0,51389 = 1
Como concluímos, a probabilidade é igual a 1, podemos notar ao sobrepormos os dois gráficos abaixo:
4. Seja X ~ N (µ; σ2).
(a) Calcule Pr(|X − µ| > kσ) para k = 1, 2, 3.
Para k=1
 X −µ

X −µ

Pr( X − µ > 1σ ) = Pr( X − µ < −σ ) + Pr( X − µ > σ ) = Pr
< −1 + Pr
> 1 =
 σ

 σ

= Pr( Z < −1) + Pr( Z > 1) = 2 × Pr( Z > 1) = 2 × [1 − Pr( Z ≤ 1)] =
= 2 × [1 − Φ (1,0] = 2 × (1 − 0,84134) = 0,31732
Para k=2
 X −µ

X −µ

Pr( X − µ > 2σ ) = Pr( X − µ < −2σ ) + Pr( X − µ > 2σ ) = Pr
< −2  + Pr
> 2 =
 σ

 σ

= Pr( Z < −2) + Pr( Z > 2) = 2 × Pr( Z > 2) = 2 × [1 − Pr( Z ≤ 2)] =
= 2 × [1 − Φ (2,0] = 2 × (1 − 0,97725) = 0,0455
Para k=3
X −µ

 X −µ

Pr( X − µ > 3σ ) = Pr( X − µ < −3σ ) + Pr( X − µ > 3σ ) = Pr 
< −3  + Pr
> 3 =
 σ

 σ

= Pr( Z < −3) + Pr( Z > 3) = 2 × Pr( Z > 3) = 2 × [1 − Pr( Z ≤ 3)] =
= 2 × [1 − Φ (3,0] = 2 × (1 − 0,99865) = 0,0027
Resposta: k=1=> 0,31732, k=2=> 0,0455 e k=3=> 0,0027
(b) Calcule o valor de k tal que Pr(|X − µ| < kσ) = 0, 95
X −µ


Pr( X − µ > kσ ) = 0,95 ⇔ Pr(− kσ < X − µ < − kσ ) = 0,95 ⇔ Pr  − k <
< k  = 0,95 ⇔
σ


= Pr(− k < Z < k ) = 0,95 ⇔ 2 × Pr(0 < Z < k ) = 0,95 ⇔ Pr(0 < Z < k ) = 0,475 ⇔ tab(k ) = 0,475 ⇔
Φ(k ) = 0,975 ⇔ k = 1,96
Resposta: k=1,96
(c) Calcule o valor de k tal que Pr(X − µ > kσ) = 0, 05
Pr( X − µ > kσ ) = 0,05 ⇔ Pr( Z > k ) = 0,05 ⇔ 1 − Φ (k ) = 0,05 ⇔ Φ (k ) = 0,95 ⇔ k = 1,64
Resposta: k=1,64
(d) Calcule o valor de k tal que Pr(X − µ < kσ) = 0, 10
Pr( X − µ < kσ ) = 0,10 ⇔ Pr( Z < k ) = 0,10 ⇔ Pr( Z > − k ) = 0,10 ⇔ 1 − Φ (− k ) = 0,10 ⇔
⇔ Φ(− k ) = 0,90 ⇔ −k = 1,28 ⇔ k = −1,28
Resposta: k=-1,28
(e) Interprete os resultados obtidos.
Podemos perceber que os resultados valem para qualquer normal.
Por exemplo, do item (a), verificamos que, para qualquer distribuição normal, o intervalo [µ − σ; µ +
σ] tem 68% de probabilidade, o intervalo [µ − 2σ; µ + 2σ] tem 95% de probabilidade e o intervalo [µ −
3σ; µ + 3σ] tem 99,7% de probabilidade.
Podemos concluir também que podemos falar em termos de número de desvios padrões, ou seja, o
desvio padrão funciona como uma medida de escala.
Como exemplo, podemos citar o item (c), que mostra que acima de 1,64 desvios padrões da média
temos sempre 5% de probabilidade.
5. Seja X o diâmetro da peça. Então, X ~ Unif(200; 52). Vamos definir os seguintes eventos:
Dp = Peça com diâmetro pequeno
Dg = Peça com diâmetro grande
P = Peça perfeita
R= Peça para refugo
(a) Qual é a probabilidade de se produzir uma peça com diâmetro pequeno?
Pr(Dp)=Pr(X<187,5)=
 X − 200 187,5 − 200 
<

 = Pr( Z < −2,5) = Pr( Z > 2,5) = 0,5 − Pr(0 < Z < 2,5) =
5
5


= 0,5 − tab(2,5) = 0,5 − 0,49379 = 0,00621
Resposta: 0,00621
(b) Qual é a probabilidade de se produzir uma peça com diâmetro dentro dos limites de
tolerância?
Pr(P)=Pr(187,5<X<215)
 187,5 − 200 X − 200 215 − 200 
Pr
<
<
 = Pr(−2,5 < Z < 3) = tab(3) + tab(2,5) = 0,49865 + 0,49379 = 0,99244
5
5
5


Resposta: 0,99244
(c) Qual é a probabilidade de se descartar uma peça como refugo?
Podemos dizer que as peças que serão descartadas como refugo são aquelas peças com diâmetro
pequeno, e as que tem 30% de probabilidade de não serem recuperadas, ou seja:
Pr(R)=Pr(Dp)+0,3Pr(Dg)
Pr (Dp) = 0,00621
Pr(Dg)=Pr(X>215) =
 X − 200 215 − 200 
= Pr
<
 = Pr( Z < 3) = 0,5 − Pr(0 < Z < 3) = 0,5 − tab(3) = 0,5 − 0,49865 = 0,00135
5
5


Pr(R) = 0,00621 + 0,3 (0,00135) = 0,00621 + 0,000405 = 0,006615
Resposta: 0,006615
(d) Sabendo que uma peça tem diâmetro dentro dos limites de tolerância, qual é a probabilidade
de que ela tenha passado pelo processo de redimensionamento?
Pr(z)=Pr(P│R) =
Pr( P ∩ R) 0,7 Pr( Dg ) 0,7 × 0,00135 0,000945
=
=
=
= 0,142857143
Pr( R)
Pr( R)
0,006615
0,006615
Resposta: 0,142857143