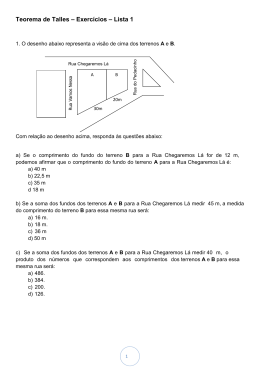
C e n tr o E d u c a c io n a l A d v e n tis ta M ilto n A fo n s o
Reconhecida Portaria 46 de 26/09/77 - SEC -DF CNPJ 60833910/0053-08
SGAS Qd.611 Módulo 75 CEP 70200-710 Brasília-DF
Fone: (61) 345-7080 Fax: (61) 345-7082
LISTA 02 DE EXERCÍCIOS DO 3º BIMESTRE 9º ANO
PROF. FABRÍCIO GARCIA
ALUNO (A): _______________________________________________TURMA: ________
1. Observe a figura e calcule as razões indicadas.

A
a)
AB

BC
b)
AB

CD
c)
AB

AD
d)
BD

AD

B

C

D
2. Os segmentos MN, PQ , RS e TU formam, nessa ordem, uma proporção. Sendo que
MN = 12 cm, RS = 4 cm e TU = 8 cm, então a medida de PQ é igual a:
a) 12 cm
b) 48 cm
c) 6 cm
d) 24 cm
3. Sejam AB e CD dois segmentos tais que AB = 2 cm e
e) 18 cm
AB
1
 . Qual a medida de CD ?
CD
3
4. Os segmentos x, y, z e w formam, nessa ordem, uma proporção. Se x = 12 m, y = 4 m e
z = 3 m, qual a medida de w?
Rua Vamos Nessa
Rua Chegaremos Lá
A
B
20 m
30 m
Rua do Pedacinho
5. O desenho abaixo representa a visão de cima dos terrenos A e B.
Com relação ao desenho acima, responda às questões abaixo:
a) Se o comprimento do fundo do terreno B para a Rua Chegaremos Lá for de 12 m, podemos
afirmar que o comprimento do fundo do terreno A para a Rua Chegaremos Lá é:
a) 40 m.
b) 22,5 m.
c) 35 m.
d) 18 m.
b) Se a soma dos fundos dos terrenos A e B para a Rua Chegaremos Lá medir 45 m, a medida do
comprimento do terreno B para essa mesma rua será:
a) 16 m.
b) 18 m.
c) 36 m.
d) 50 m.
c) Se a soma dos fundos dos terrenos A e B para a Rua Chegaremos Lá medir 40 m, o produto
dos números que correspondem aos comprimentos dos terrenos A e B para essa mesma rua será:
a) 486.
b) 384.
c) 200.
d) 126.
6. Dado um segmento RQ , determine um ponto P  RQ , distante 6 cm de R. Sabendo-se que
PR
3

, qual a medida de RQ ?
PQ 10
7. Sabendo que a // b // c, determine o valor x:
a)
a
3
n
b)
a
b
c
6
5
x+2
x
b
4
8
c
8. Sabendo que a // b // c, determine o valor x :
a)
a
b)
a
b
c
x
9
12
8
b
x+2
x+4
6
24
c
c)
a
2x
x+1
8
12
b
c
9. As retas r1, r2 e r3 são paralelas e os comprimentos dos segmentos de transversais são
indicados na figura. Então x é igual a:
a)
21
5
x
b) 7,5
6
5
c) 6
d)
15
8
5
r1
r2
3
r3
e) 1
10. Determine os valores de x e y nos seguintes feixes de paralelas:
x
21
2
y
4
5
9
x
52
y
12. Calcule o valor de x, y e t, na figura abaixo, sabendo que r // s // t // u.
r
6
y
t
10
x
4
5
s
t
12
u
13. (FEI-SP) Na figura DE // BC. Então, o valor de x é:
A
a) 4
x
b) 6
c) 14
10
D
d) 9
E
x+3
15
e) 2
C
B
14. (UPF-RS) A figura mostra um esquema, no qual DE // BC , AB = 20 cm, BD = 16 cm e
CE = 20 cm.
C
A
E
B
D
15. Na figura abaixo, a // b // c. Qual o valor de x e y?
a
18
15
x
10
b
5
y
c
16. No ABC da figura, CD é a bissetriz do ângulo Ĉ . Se AD = 3 cm, DB = 2 cm e AC = 6 cm,
determine:
C
a) a medida do lado BC.
b) o perímetro do ABC.
A
D
B
17. Observando o desenho abaixo, temos que AD é bissetriz do ângulo Â. Podemos afirmar
corretamente que x é:
a) 16
A
30
b) 32
c) 64
20
d) 86
e) 72
D
x
40
18. (UCSAL-BA) Na figura abaixo, as medidas assinaladas são dadas em centímetros, e AB // DE .
Se BD = 7 cm, então x é igual a:
A
B
4
a) 1,2
x
C
b) 1,8
c) 2,1
6
d) 2,4
e) 2,8
D
E
19. Uma reta paralela ao lado BC de um triângulo ABC determina o ponto D em AB e um ponto E
em AC. Sabendo-se que AD = x, DB = x + 6, AE = 2 cm e EC = 4 cm, então o valor do lado
AB desse triângulo é:
a) 9 cm
b) 13 cm
c) 15 cm
d) 20 cm
e) 18 cm
20. Na figura abaixo, BD é bissetriz, AD = 8 cm, CD = 10 cm. Sendo AB = 3x e BC = 4x – 3,
então o valor do perímetro desse triângulo é igual a:
a) 99 cm.
B
b) 67 cm.
c) 50 cm.
4x – 3
3x
d) 18 cm.
e) 32 cm.
8
A
10
D
C