. Opções Reais em Petróleo:
Uma Visão Geral
Seminário na Escola Politécnica, DEI, UFRJ
Rio de Janeiro, 16 de Setembro de 2003
Por: Marco Antonio Guimarães Dias
Petrobras/E&P-Corp/EngP/DPR
Visite o 1o website de opções reais: www.puc-rio.br/marco.ind/
Tópicos do Seminário
 Introdução
e visão geral de opções reais em
exploração e produção (E&P) de petróleo

Intuição, modelo clássico, processos estocásticos p/ preços do óleo
 Aplicações
no Brasil de opções reais em petróleo

Política de timing do setor petróleo (opções extendíveis)
 Programa de pesquisa da Petrobras “PRAVAP-14”
Valoração de Projetos de Desenvolvimento sob Incertezas
Projetos
internos e externos (especialmente PUC-Rio).
 Investimento

em informação, opções reais e revelação
Combinação de incertezas técnicas (volume e qualidade da
reserva) e de mercado (preços do petróleo)
Visão Gerencial de Opções Reais (OR)
 OR
é uma metodologia moderna para análise econômica
de projetos e decisões de investimento sob incerteza


OR complementa (não substitui) as ferramentas corporativas (ainda)
Difusão corporativa de OR toma tempo e treinamento
 Considera
as incertezas e as opções (flexibilidades
gerenciais) relevantes e dá duas respostas:


o valor da oportunidade de investimento (o valor da opção)
a regra de decisão ótima (gatilho)
 Pode
ser visto como um problema de otimização:
 Maximizar
o VPL (função objetivo típica), sujeito a:
 (a) Opções (flexidades gerenciais) relevantes;
 (b) Incertezas de mercado (ex.: preço do óleo, demanda);
 (c) Incertezas técnicas (ex.: reserva de óleo);
 (d) Incerteza nas ações de outros players (competição).
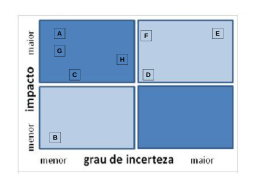
Quando as Opções Reais São Valiosas
Baseado no livro “Opções Reais” de Copeland & Antikarov
Opções reais tem valor quanto maior for a incerteza e a flexibilidade de reação
Baixa
Baixa
Probabilidade de receber nova informação
Incerteza
Alta
Espaço para a
flexibilidade gerencial

Capacidade de reagir

Flexibilidade de
valor moderado
Flexibilidade
de alto valor
Flexibilidade
de valor baixo
Flexibilidade de
valor moderado
Alta
Principais Tipos de Opções
Opção de Espera (de “Timing”)

Aguarda novas informações e aprende.
Espera proativa. Ex.: desenvolvimento inicial.
Opção Seqüencial e de Expansão
 Valora o aspecto “estratégico”

Ex.: Poços opcionais podem ser perfurados
Opção de Abandono

Gerentes não são obrigados a seguir um plano
de negócios se ele se tornar não-lucrativo.

O programa de investimento seqüencial (ex.:
delimitação de um campo) pode ser abandonado se a
informação gerada nesse processo for desfavorável.
Processo de Opções Reais Seqüenciais em Petróleo E&P
Probabilidade de sucesso
de óleo/gás = p
Volume Esperado
de Reservas = B
Reserva
Esperada = B’
 Bloco (prospecto): Opção de perfurar o pioneiro
Investimento em
Exploração
 Campo Não Delimitado: Opção de delimitar
Investimento em
Delimitação
 Reservas Não-Desenvolvidas: Opções de
investir em informação adicional e desenvolver
Investimento em
Desenvolvimento
 Reservas Desenvolvidas: Opções de expansão
(adicionar poços extras, adensar malha, etc.);
de interromper a produção e de abandonar
Qualidade Econômica da Reserva Desenvolvida

Imagine que você quer comprar 100 milhões de barris de
reservas desenvolvidas. Assuma que o preço de longo-prazo do
petróleo é de 20 US$/bbl.
 Quanto você pagaria por barril de reserva desenvolvida?
 Isso depende de vários fatores tais como a qualidade permo-porosa da
rocha (produtividade), qualidade dos fluidos (óleo pesado x leve, etc.), país
(regime fiscal, risco político), localização específica da reserva (águas
profundas tem maior custo operacional que as reservas onshore), o capital
in place (velocidade de extração e logo o valor presente da receita depende
do número de poços), etc.

Quanto maior é o valor do barril de reserva em relação ao
barril de óleo (na superfície), maior é a qualidade econômica:
valor de um barril de reserva = v = q . P



Onde q = qualidade econômica da reserva desenvolvida
O valor da reserva desenvolvida é v vezes o tamanho da reserva (B)
Logo, vamos usar a equação para o VPL = V - D = q P B - D
D
= custo de desenvolvimento (investimento ou preço de exercício da opção)
VPL (milhões $)
Qualidade da Reserva e Gráfico do VPL
Equação Linear para o VPL
usando o “Business Model”:
VPL = q P B - D
VPL em função de P
valor da planilha de FC
tangente q = q . B
P ($/bbl)
-D
A qualidade da reserva (q) está relacionada
com a inclinação do gráfico VPL x P
Intuição (1): Opção de Timing e Valor da Jazida

Assuma a equação simples para o VPL de desenvolvimento:



VPL = q B P - D = 0,2 x 500 x 18 – 1850 = - 50 milhões $
Você venderia esse campo de petróleo por US$ 3 milhões?
Suponha o seguinte problema em dois períodos e só dois cenários no
segundo período para o preço do óleo P representando a incerteza.
t=1
E[P+] = 19  VPL+ = + 50 milhões $
50%
t=0
E[P] = 18 $/bbl
VPL(t=0) = - 50 milhões $
50%
E[P-] = 17  VPL- = - 150 milhões $
Gerente racional não irá exercer essa
opção  Max (VPL-, 0) = zero
Logo, em t = 1 o VPL do projeto é positivo: (50% x 50) + (50% x 0) = + 25 milhões $
Intuição (2): Opção de Timing e Valor da Espera

Suponha o mesmo caso mas com um VPL um pouco positivo.
O que é melhor: desenvolver agora ou “esperar e ver”?


VPL = q B P - D = 0,2 x 500 x 18 – 1750 = + 50 milhões $
Taxa de Desconto = 10%
t=1
E[P+] = 19  VPL+ = + 150 milhões $
50%
t=0
E[P] = 18 /bbl
VPL(t=0) = + 50 milhões $
50%
E[P-] = 17  VPL- = - 50 milhões $
Gerente racional não irá exercer essa
opção  Max (VPL-, 0) = zero
Logo em t = 1, o VPL do projeto é: (50% x 150) + (50% x 0) = + 75 milhões $
O valor presente é: VPLespera(t=0) = 75/1,1 = 68.2 > 50
Logo é melhor “esperar e ver”, exercendo a opção somente no cenário favorável
Intuição (3): Opção Real “Deep-in-the-Money”
 Suponha



o mesmo caso mas com um VPL bem maior.
O que é melhor: desenvolver agora ou “esperar e ver”?
VPL = q B P - D = 0,25 x 500 x 18 – 1750 = + 500 milhões $
t=1
Taxa de Desconto = 10%
E[P+] = 19  VPL+ = 625 milhões $
50%
t=0
E[P] = 18 /bbl
VPL(t=0) = 500 milhões $
50%
E[P-] = 17  VPL- = 375 milhões $
Logo, em t = 1 o VPL do projeto é: (50% x 625) + (50% x 375) = 500 milhões $
O valor presente é: VPLesperar(t=0) = 500/1,1 = 454.5 < 500
O exercício imediato é ótimo porque esse projeto está deep-in-the-money (alto VPL)
Para que valor da reserva V* (gatilho) se ficaria indiferente entre esperar e investir?
Modelo Clássico de Opções Reais em Petróleo
 Paddock
& Siegel & Smith escreveram uma série de
artigos sobre valoração de reservas offshore nos anos 80



É o modelo mais conhecido para decisões de desenvolver jazidas
Explora a analogia opções financeiras com opções reais
Incerteza em V é modelada com o movimento geométrico Browniano
Opções Financeiras: Black&Scholes-Merton
Valor da Opção Financeira
Opções Reais: Paddock, Siegel & Smith
Valor da Reserva Não-Desenvolvida (Opção Real) (F)
Preço Corrente da Ação
Valor Corrente da Reserva Desenvolvida (V)
Preço de Exercício da Opção
Investimento para Desenvolver a Reserva (D)
Taxa de Dividendo da Ação
Fluxo de Caixa Líquido de Depleção/V (d)
Taxa de Juros Livre de Risco
Taxa de Juros Livre de Risco (r)
Volatilidade da Ação
Volatilidade do Valor da Reserva Desenvolvida (s)
Tempo de Expiração da Opção
Tempo de Expiração dos Direitos de Investir (t)
Equação da Reserva Não-Desenvolvida (F)
 Equação
Diferencial Parcial (t, V) para o valor da opção F
0.5 s2 V2 FVV + (r - d) V FV - r F = - Ft
 Condições
de Contorno da EDP:
Ação Gerencial É
Inserida no Modelo

Para V = 0, F (0, t) = 0
 Para t = T, F (V, T) = max [V - D, 0] = max [VPL, 0]
Para V = V*, F (V*, t) = V* - D
 “Contato Suave”, FV (V*, t) = 1

 Parâmetros: V =
}
Condições no Ponto em que é
Ótimo o Imediato Investimento
valor da reserva desenvolvida (ex., V = q P B);
D = custo de desenvolvimento; r = taxa de desconto livre de risco;
d = taxa de dividendos para V ; s = volatilidade of V
O Valor dos Direitos (F) de Investir na Jazida
Assuma que V = q B P, podendo usar o gráfico F x V ou F x P
 Suponha que o “break-even” (NPV = 0) de desenvolver é US$15/bbl
Curva do Gatilho: A Regra de Decisão Ótima
 Analogamente,
pode-se pensar no gatilho V* ou no
gatilho P* (se V é ~ proporcional a P), V* = q B . P*
Estimando os Parâmetros do Modelo
 Se V =

k P, então sV = sP e dV = dP (D&P p.178. Por que?)
Geométrico Browniano Neutro ao Risco: dV = (r - dV) V dt + sV V dz
 Volatilidade

dos preços do óleo no longo-prazo (~ 20% p.a.)
Para decisões de desenvolvimento, o valor do benefício é ligado
aos preços de longo-prazo, não os (mais voláteis) preços spot

Um proxy de mercado é o contrato de mais longa maturidade do
mercado futuro, que tenha liquidez (Nymex mês 18; Brent mês 12)
 Volatilidade = desvio padrão de( Ln Pt - Ln Pt-1 )

Dividend yield (ou convenience yield de longo-prazo) ~ 6% p.a.


Paddock & Siegel & Smith: equação usando fluxos de caixa
Se V = k P, podemos estimar d do mercado futuro de petróleo
 Regra

de Pickles & Smith (1993): r = d (no longo-prazo)
“We suggest that option valuations use, initially, the ‘normal’ value of net convenience
yield, which seems to equal approximately the risk-free nominal interest rate”
Brent: Preços Spot x Preço Futuro
 Note
que os preços spot (“à vista”) alcançam valores mais
extremos que os preços do mercado futuro
Brent Prices: Spot (Dated) vs. IPE 12 Month
Jul/1996 - Jan/2002
40
Brent Platt's Dated Mid (US$/bbl)
Brent IPE Mth12 Close (US$/bbl)
35
Brent (US$/bbl)
30
25
20
15
10
1/22/2002
10/22/2001
7/22/2001
4/22/2001
1/22/2001
10/22/2000
7/22/2000
4/22/2000
1/22/2000
10/22/1999
7/22/1999
4/22/1999
1/22/1999
10/22/1998
7/22/1998
4/22/1998
1/22/1998
10/22/1997
7/22/1997
4/22/1997
1/22/1997
10/22/1996
5
7/22/1996
Estrutura à Termo
Mercado Futuro Brent
Movimento Geométrico Browniano (MGB)
 Um
processo estocástico pode ser visto como um
mapeamento de probabilidades ao longo do tempo.

No caso do MGB, a tendência é um crescimento (ou queda)
exponencial e os preços tem uma distribuição lognormal com
variância crescendo com o horizonte temporal.
Variância cresce com
o horizonte de previsão
Distribuição de
probabilidades
log-normal
tendência
ou drift
(aqui a > 0)
Reversão à Média de Longo Prazo
 No
caso do processo de reversão à média, a tendência é o
preço reverter para um nível de equilíbrio do mercado, P,
chamada de média de longo prazo. Analogia: mola.

Nesse caso a variância cresce inicialmente e depois se estabiliza
 Gráficos mostram as variâncias em ti @ tj @ tk (estáveis após ti )
Caso P0 < P
Tendência do preço subir
Caso P0 > P
Tendência do preço cair
Alternativas de Processos Estocásticos para Preços do Óleo

Existem vários modelos de processos estocásticos para preços do
óleo na literatura de opções reais. Eu classifico eles em três classes

As propriedades adequadas do Movimento Geométrico Browniano (poucos
parâmetros, homogeneidade) é um grande incentivo prático para seu uso.
 Pindyck (1999) escreveu: “é improvável que a premissa do MGB leve
a erros significativos na regra ótima de investimento”
Processo de Jump-Reversão: os Sample Paths

O gráfico mostra 100 caminhos (sample paths) de uma simulação de
Monte Carlo para um processo de reversão com jumps de um óleo
pesado com P = 15 $/bbl. Freqüência de jumps 1 a cada 5 anos.
Jump-Reversion Sample Paths
Preços Nominais do Óleo Brent ou Similar (1970-2003)

Vemos os preços do óleo com saltos (jumps) em ambas direções,
dependendo do tipo de notícia anormal: jumps-up em 1973/4, 1978/9,
1990, 1999, 2002; e jumps-down em 1986, 1991, 1997, e 2001
Jumps-up
Jumps-down
Reversão à Média com Saltos: Dias & Rocha

Nós (Dias & Rocha, 1998/9) adaptamos a idéia de difusão-saltos
de Merton (1976) para o caso de preço de óleo, considerando:


Notícias normais causam só ajustes marginais nos preços do óleo,
modelado com um processo tempo-contínuo de reversão à média
Notícias raras anormais (guerra, surpresas da OPEP, ...) causam
ajustes anormais (saltos) nos preços do óleo, modelados com um
processo de Poisson (jumps-up & jumps-down em tempo-discreto)
 Um
processo similar de reversão à média com saltos foi
usado por Dias para remunerar o equity (US$ 200 MM)
do Project Finance de Marlim (oil prices-linked spread)

Ganha-Ganha (maior preço do óleo  maior spread, e vice versa)

Contrato foi em dezembro/98 quando o preço do óleo era 10 US$/bbl
 A curva
de valor esperado era uma rápida reversão para US$ 20/bbl
 Com a possibilidade de saltos, nós colocamos cap e floor no spread
– Essa visão de saltos foi muito importante pois poucos meses depois os preços
do óleo saltaram, dobrando de valor em agosto/99: cap protegeu a Petrobras
Política de Timing para o Setor Petróleo
 A abertura
do setor petróleo brasileiro começou em 1997,
quebrando o monopólio da Petrobras. Para o E&P:


Regime fiscal de concessões, com leilão selado de 1o preço
Adotado o conceito de opções extendíveis (dois ou três períodos).
 A extensão
do prazo é condicional a um compromisso exploratório
adicional (1-3 poços), estabelecido antes do leilão (bid)

A possibilidade de extensão ocorre também nos EUA (5 + 3 anos,
em algumas áreas do GoM) e na Europa (paper da Kemna, 1993)
 Opções com maturidades extendíveis foi estudado por Longstaff
(1990) para aplicações financeiras
 O timing da fase exploratória (tempo de expiração para os
direitos de desenvolvimento) foi objeto de um debate público
 A agência
(ANP) postou o primeiro projeto para debate em seu website
em fevereiro/98, com 3 + 2 anos, tempo considerado muito curto
 Dias
& Rocha escreveram um paper sobre isso apresentado em maio/98.
Opções de Maturidade Extendível:
Caso de Dois Períodos
Período
T E M P O
t = 0 a T1:
1o
Período
T1: 1a
Expiração
T1 a T2:
2o
Período
T2: 2a
Expiração
Opções Disponíveis
[Desenvolver Já] ou [Espere e Veja]
[Desenvolver Já] ou [Estender (paga K)]
ou [Abandonar (Retorna ao Governo)]
[Desenvolver Já] ou [Espere e Veja]
[Desenvolver Já] ou
[Abandonar (Retorna ao Governo)]
Valor da Opção na Primeira Expiração
 Na
primeira expiração (t = T1), a firma pode desenvolver o
campo, estender a opção ou abandonar/devolver o bloco
para a ANP/governo
 Para o caso base do Movimento Geométrico Browniano:
Debate da Política de Timing do Setor Petróleo

As companhias de petróleo consideraram muito curto o prazo
exploratório de 3 + 2 anos do anteprojeto da ANP

Isso estava abaixo da prática international principalmente para
águas profundas (ex.: EUA/GoM: areas com ou 5 + 3 ou 10 anos)
 Durante 1998 e parte de 1999, o Diretor da ANP insistiu nessa
política de prazo curto, mesmo com a reclamação das firmas
 As simulações numéricas do nosso paper (Dias & Rocha, 1998)
concluíram que o timing ótimo deveria ser de 8 a 10 anos
 Em janeiro de 1999 nós enviamos o nosso paper para o influente
deputado e ex-Ministro Delfim Netto, destacando essa conclusão
 Em abril/99 (3 meses antes do 1o bid), Delfim Netto escreveu
um artigo na Folha de São Paulo defendendo um prazo maior
para a política de timing do setor petróleo
 Delfim usou as conclusões do nosso paper para suportar a sua visão!
 Poucos dias depois, finalmente o diretor da ANP mudou de posição!

Desde o 1o bid a maioria das áreas tem 9 anos. No mínimo uma coincidência!
Alternativas de Política de Timing em Dias & Rocha
 A tabela
abaixo mostra a análise de sensibilidade para
diferentes políticas de prazo para o setor petróleo

Valores de opção (F) são proxy para o bônus no leilão
 Maior o gatilho (P*), maior o adiamento dos investimentos
Trade-off:
maiores prazos significam mais bônus mas mais espera
 Tabela
indica um maior ganho % para o valor da opção
(bônus) do que o % de aumento no gatilho (adiamento)

Logo, é razoável considerar algum valor entre 8-10 anos
PRAVAP-14: Alguns Projetos de Opções Reais

PRAVAP-14 é um programa de pesquisa sistêmico chamado de
Valoração de Projetos de Desenvolvimento sob Incertezas


Eu coordeno esse projeto sistêmico pelo E&P-Corporativo
Apresentaremos alguns projetos de opções reais desenvolvidos:

Revelação Exploratória com foco em bids (pre-PRAVAP-14)
 Valor dinâmico da Informação para projetos de desenvolvimentos
 Seleção de alternativas mutuamente exclusivas de
desenvolvimento sob incertezas de preços do óleo (com PUC-Rio)
 Análise de alternativas de desenvolvimento com opção de expansão,
considerando incertezas técnicas e nos preços do óleo (com a PUC)
 Analisamos diferentes processos estocásticos e métodos de solução



Geométrico Browniano, reversão + saltos, diferentes modelos de reversão
Diferenças finitas, Monte Carlo para opções americanas, algoritmos genéticos
Algoritmos genéticos são usados para otimização (evolução de curvas de gatilho)
 Eu chamo esse método de opções reais evolucionárias (tenho 2 papers)
Incerteza Técnica e Valor

Incerteza técnica tem correlação zero com a carteira de mercado.
Logo o prêmio de risco incremental é zero


A taxa de desconto é a mesma se o projeto possui incerteza técnica ou não,
uma vez que os acionistas são investidores diversificados
Entretanto, incerteza técnica diminui tanto o valor presente
líquido (VPL) dos projetos como o valor das opções reais

A incerteza técnica quase certamente levará ao exercício da opção errada
de projeto de desenvolvimento (capacidade da planta, no de poços,
localização dos poços, e até padrões de segurança inadequados)
O
projeto sub-ótimo gera ou over-investimento ou sub-investimento quando
comparado com o nível ótimo de investimento que maximiza o VPL ou OR



A incerteza técnica levará ao exercício da opção quando o melhor é não
exercer a opção (“esperar e ver” é melhor para o verdadeiro valor)
A incerteza técnica levará ao não exercício da opção quando o melhor é
exercer a opção (opção deep-in-the-money para o verdadeiro valor)
Logo a incerteza técnica diminui valor devido a decisões subótimas, e não devido à taxa de desconto ou “utilidade do gerente”
Incerteza Técnica: Ameaça e Oportunidade
 Incerteza
técnica gera a ameaça de exercício sub-ótimo da
opção desenvolvimento. Mas isso é somente um lado da moeda.
 Incerteza técnica cria também uma oportunidade: gera a opção
de investir em informação antes da decisão de desenvolvimento
(a opção de aprendizagem é valiosa)
VPL Esperado
• O valor de aprendizagem será capturado pelo modelo de opções
•Usaremos uma equação D(B) para o investimento ótimo de desenv.
Informação Imperfeita ou Revelação Parcial
 Nova
informação reduz a incerteza técnica mas usualmente
alguma incerteza residual permanece (revelação parcial)

Nesse caso nós temos 3 distribuições a posteriori. Para o caso com
cenários contínuos nós temos infinitas distribuições a posteriori!

É muito mais simples trabalhar com a única distribuição de expectativas
condicionais (que será chamada de distribuição de revelações)
Expectativa Condicional na Teoria e na Prática

Vamos responder o questionamento sobre a relevância do conceito
de expectativa condicional para valorar aprendizagem


No último slide nós vimos que é muito mais simples trabalhar com a única
distribuição de expectativa condicional que várias distribuições posteriores
Outra vantagem prática: valor esperado tem um lugar natural em finanças

Firmas usam as expectativas correntes para calcular o VPL ou o resultado do exercício da
opção real. Ex-ante o investimento em informação, a nova expectativa é condicional
 O preço dum derivativo é simplesmente uma expectativa de valores futuros (Tavella, 2002)

O conceito de expectativa condicional é também sonoro teoricamente:
 Queremos
estimar X observando I, através da função g( I ).
 A medida de qualidade dum preditor mais usada é o erro médio quadrático
definido por MSE(g) = E[X - g( I )]2 . A escolha de g* que minimiza a medida de
erro MSE(g) é exatamente a expectativa condicional E[X | I ].
 Essa é uma propriedade muito conhecida e usada em econometria

Mesmo na literatura de análise de decisão, é comum trabalhar com
expectativa dentro da equação de maximização (ex., McCardle, 1985)
 Mas
em vez de focar nas propriedades das expectativas condicionais, o foco dessa
literatura tem sido de inferência estatística focado na função verosimilhança.
 Se
privilegia a análise de dados e não o valor ex-ante dum projeto de obter informação
Revelação de Informação & Distribuição de Revelações

Revelação (definição): processo em direção à verdade

O processo de acumulação de dados sobre um parâmetro técnico X incerto é
um processo de aprendizagem em direção à “verdade” sobre X
 Isso




sugere os nomes de revelação de informação e distribuição de revelações
Um conceito similar mas não igual é o “princípio da revelação” usado em
jogos Bayesianos referente à verdade sobre o tipo de um jogador.
Aqui estamos interessados na verdade sobre um parâmetro técnico
Isso significa que se investirmos o suficiente em informação, podemos saber a
verdade a respeito desses parâmetros técnicos (ex.: volume da reserva)
Valorando um projeto de investimento em informação, E[X | I], a
expectativa conditional do parâmetro X, é uma variável aleatória
 A distribuição de expectativas condicionais E[X | I] é aqui chamada de
distribuição de revelações, isto é, a distribuição de RX = E[X | I]
 A distribuição de revelações tem atraentes propriedades práticas
 Usaremos
a distribuição de revelações em simulações de Monte Carlo, a fim
de combinar com outras fontes de incerteza numa abordagem neutra ao risco
 A distribuição
de revelações já é uma distribuição neutra ao risco já que a incerteza
técnica não demanda prêmio de risco e assim não requer ajuste adicional ao risco
Incerteza Técnica e Bacias Pouco Exploradas

Seja uma bacia pouco explorada onde várias firmas irão investir em
sísmica e em poços pioneiro ao longo dos próximos anos
 Informação pode ser tanto custosa (nosso investimento) e/ou grátis,
advinda do investimento de outras firmas (free-rider)
Investimento
em informação
(sísmica, etc.)
.
t=0
Avaliação
técnica e
econômica
hoje

Investimento em informação
(custoso e free-rider)
t=T
t=1
Possíveis cenários depois
da chegada da informação
durante o primeiro ano do
período exploratório
Distribuição
de Revelações
Possíveis
cenários
depois do
revelation de
informação
durante todo
o período da
exploração
A dinâmica do processo de informação alavanca o valor de opção do bloco
Combinação de Incertezas com Monte Carlo
 Considerando
que: (a) existem muitas incertezas nessa bacia
pouco conhecida; e (b) muitas companhias de petróleo irão
perfurar poços naquela área nos próximos 5 anos:

As expectativas em 5 anos quase certamente irão mudar e também o valor do bloco
As distribuições de revelações e a distribuição neutra ao risco do preço do óleo são:
Distribuições de Expectativas
(distribuições de revelações)

Simulação Real x Simulação Neutra ao Risco

Os caminhos simulados do MGB: um real (drift a) e o outro neutro ao
Real Versus
risco (r - d). Na realidade
r - dRisk-Neutral
= a - p, ondeSimulations
p é um prêmio de risco
45
Real Simulation
40
Risk-Neutral Simulation
35
25
20
15
10
5
Time (Years)
6.
0
5.
8
5.
5
5.
3
5.
0
4.
8
4.
5
4.
3
4.
0
3.
8
3.
5
3.
3
3.
0
2.
8
2.
5
2.
3
2.
0
1.
8
1.
5
1.
3
1.
0
0.
8
0.
5
0.
3
0
0.
0
Oil Price ($/bbl)
30
Equação Visual para Opções Reais
 Hoje o VME do prospecto é negativo, mas existem 5 anos para a decisão de perfurar o
poço pioneiro e novos cenários serão revelados pela atividade exploratória na bacia.
+
Valoração do Prospecto
(em milhões $)
Valor Tradicional = - 5
=
Valor de Opção (T) = + 12,5
Valor de Opção (@ t=0) = + 7,6
Logo, se oferecerem $3 milhões, recuse!
E&P: Processo de Opções Seqüenciais
Probabilidade de
Sucesso Óleo/Gas = p
Volume de Reservas
Esperada = B
Volume
Revisado = B’
 Perfura
o pioneiro? Espera? Estende?
 Modelo de Incerteza Técnica é requerido
 Fase
appraisal: delimitação de reservas
 Deve-se investir em informação adicional?


Reservas Delineadas mas Não-Desenvolvidas
Desenvolver? Aguardar melhores condições?
Estender? Qual a melhor alternativa?
 Reservas

Desenvolvidas.
Expandir a produção? Vender a reserva madura?
Parar temporariamente? Abandonar?
Redução de Incerteza e Distribuição de Revelações


Intuitivamente, o objetivo gerencial de um investimento em
informação é reduzir a incerteza técnica (aprendizagem)
Pelo lado do benefício, a qualidade de um projeto de investimento
em informação é relacionado com o poder de revelação do projeto
 Uma
alternativa mais cara de investimento em informação pode ser preferível se tiver
maior capacidade de reduzir a incerteza, isto é, maior poder de revelação
 Nós precisamos de um modelo simples que quantifique o valor de reduzir a incerteza

Precisamos distinguir os benefícios de projetos mutuamente exclusivos de aprendizagem

Isso será obtido com as atraentes propriedades da distribuição de
revelações que permitirá comparar alternativas com diferentes
poderes de revelação. Apresentaremos as 4 proposições práticas.
 Estarão ligados a redução esperada de incerteza com a
dispersão (variância) da distribuição de revelações?

A resposta é sim e duma maneira muito simples! (Proposição 3)
 A redução

esperada de variância é igual à variância da distribuição de revelações
Como a volatilidade, a variância da distribuição de revelações alavanca o valor da opção
Propriedades da Distribuição de Revelações

A distribuição de revelações RX (distribuição de expectativas condicionais
à nova informação) tem ao menos 4 propriedades práticas de interesse:

Proposição 1: para o caso de revelação total, a distribuição de revelações RX é
igual a distribuição incondicional (ou distribuição a priori ) de X
 Essa

Proposição 2: O valor esperado para a distribuição de revelações é igual ao
valor esperado da distribuição original (ou a priori) do parâmetro X


é a propriedade de RX no limite de um processo de aprendizagem
E[E[X | I ]] = E[RX] = E[X] (conhecido como lei das expectativas iteradas)
Proposição 3: a variância da distribuição de revelações é igual a redução de
variância esperada induzida pela nova informação
| I ]] = Var[RX] = Var[X] - E[Var[X | I ]] = Redução de Variância
Esperada (essa propriedade reporta o poder de revelação de uma alternativa)
 Var[E[X
 Ou:

Var[RX] = redução percentual esperada da incerteza x Var[X]
Proposição 4: Num processo sequencial de investimento em informação, a
sequencia {RX,1, RX,2, RX,3, …} é um martingale dirigido por eventos
 Em
resumo, ex-ante essas variáveis aleatórias tem o mesmo valor esperado
Investimento em Informação e Cenários Revelados
 Suponha
o seguinte exemplo estilizado de projeto de
delimitação de um campo para ilustrar as proposições

O poço perfurado na área “a” provou 100 MM bbl (MM = milhões)
Área a: provada
Ba = 100 MM bbl
Área c: possível
50% de chances de
Bc = 100 MM bbl
e 50% de nada ter

a
c
b
Área b: possível
50% de chances de
Bb = 100 MM bbl
e 50% de nada ter
d
Área d: possível
50% de chances de
Bd = 100 MM bbl
e 50% de nada ter
Suponha que existam três alternativas de investimento em informação
com diferentes poderes de revelação: (1) perfurar um poço (na área b);
(2) perfurar dois poços (b + c); (3) perfurar três poços (b + c + d)
Visualização dos Cenários Revelados: Distribuição de Revelações
Alternativa 1
.
t=0
E1(B) = 300
E(B) = 250
(MM boe)
E2(B) = 200
Informação (2 poços)
E1(B) = 350
.
t=0
Alternativa 2
E(B) = 250
(MM boe)
E2(B) = 250
E3(B) = 150
Informação (3 poços)
E1(B) = 400
.
t=0
Alternativa 3
(full revelation) E(B) = 250
(MM boe)
E2(B) = 300
E3(B) = 200
E4(B) = 100
Essa é exatamente a distribuição a priori de B (Prop. 1 OK!)
Todas as distribuições de revelações tem a mesma média (maringale): Prop. 4 OK!
Informação (1 poço)
Distribuições a Posteriori x Distribuição de Revelações

Maior volatilidade, maior valor da opção. Por que investir para reduzir a incerteza?
Por que aprender?
Redução de
incerteza
técnica

Distributições
de expectativas
condicionais
Aumenta a
variância da
distribuição de
revelações
(e, logo, o
valor da opção)
 Valor
Valor Dinâmico da Informação
da informação tem sido estudado pela teoria de análise
de decisão. A extensão aqui apresentada usando opções
reais, adota o nome valor dinâmico da informação.

Por que dinâmico? Porque considera a variável “tempo”:
 Tempo
de expiração ANP para a Petrobras se comprometer com o PD;
 Time to learn: o processo de aprendizagem consome tempo. Tempo de coletar
dados, processá-los, e analizá-los, para obter novo conhecimento técnico;
 Processo estocástico em tempo contínuo para as incertezas de mercado (preço
do óleo) interagindo com as expectativas revisadas de parâmetros técnicos

O especialista de reservatórios precisa responder duas questões:
 Qual a incerteza total de cada parâmetro técnico relevante? Ou seja,
quais são os parâmetros das distribuições de probabilidades a priori?
 Para cada alternativa de investimento em informação, qual é a % de
redução de variância esperada em cada parâmetro técnico?


Isso é o mínimo que se precisa saber ao se propor investir em informação,
incerteza atual e expectativa de redução da mesma investindo em informação
Precisaremos também de uma função otimização de investimento
Equações para o VPL de Desenvolvimento

Vamos ver um exemplo. Quando a opção de desenvolvimento é
exercida, obtém-se o valor presente líquido (VPL) dada pela equação:
VPL = V - D = q P B - D

A combinação de incertezas é feita com a simulação de Monte Carlo
q

= qualidade econômica da reserva, que tem incerteza técnica
(modelada com a distribuição de revelações);
 P(t) é a expectativa de longo prazo do preço do óleo, fonte de incerteza de
mercado, modelada com um processo estocástico neutro ao risco;
B = volume da reserva (milhões de barris), que tem incerteza técnica; e
D = investimento de desenvolvimento, funcão do tamanho da reserva B
Depois da revelação de informação, assuma que a escolha da capacidade
ótima é função só do volume de reservas. Essa função otimização é:
D(B) = Custo Fixo + Custo Variável x B
Logo,
o investimento ótimo de desenvolvimento D muda depois da
revelação de informação a respeito do volume de reserva B.
Outra otimização é referente ao timing de investimento (opções reais)
Real x Risk-Neutral Simulation

Simulation paths for the geometric Brownian motion: one using
the real drift (a) and the other risk-neutral drift (r - d).

It is easy to show that the risk-neutral drift r - d = a - p where p is the risk-premium
The simulation equations are:
Real Versus Risk-Neutral Simulations
45
Real Simulation
40
Risk-Neutral Simulation
35
30
25
20
15
10
5
Time (Years)
6.
0
5.
8
5.
5
5.
3
5.
0
4.
8
4.
5
4.
3
4.
0
3.
8
3.
5
3.
3
3.
0
2.
8
2.
5
2.
3
2.
0
1.
8
1.
5
1.
3
1.
0
0.
8
0.
5
0.
3
0
0.
0
Oil Price ($/bbl)

Combinação de Incertezas, VoI e Opções Reais

O investimento DP ótimo se dá quando o valor simulado de V/D alcança o gatilho (V/D)*
VPLDP = V - D(B) = q B P - D(B)
Normalização: V/D = q B P / D(B)
A
B
Valor Presente (t = 0)
F(t = 0) =
= F(t=1) * fator de desconto(t)
Opção F(t = 1) = V - D
Pular para as conclusões?
F(t = 2) = 0
Expirou
Sem Valor
Melhor Alternativa de Investimento em Informação

Dado o conjunto k = {0, 1, 2… K} de alternativas (k = 0 denota
não investir em informação) a melhor, k*, é a que maximiza Wk
 Onde Wk
é o valor da opção real incluindo o custo/benefício
do investimento em informação com a alternativa k (custo
de aprender Ck, tempo de aprender tk), dado por:

Onde EQ é a expectativa sob medida neutra ao risco, a qual é
avaliada com a simulação de Monte Carlo, e t* é o tempo
ótimo de exercício (stopping time). Para o caminho i:
Pular para as conclusões?
E&P Process and Options
Oil/Gas Success
Probability = p
 Drill
Expected Volume
of Reserves = B

Revised
Volume = B’
the wildcat? Wait? Extend?
Revelation, option-game: waiting incentives

Appraisal phase: delineation of reserves
 Technical uncertainty: sequential options

Delineated but Undeveloped Reserves.
 Wait and See? Invest in information?
Develop? What is the best alternative?

Developed Reserves.
 Expand the production?
 Stop Temporally? Abandon?
Selection of Alternatives under Uncertainty
 In
the equation for the developed reserve value V = q P B,
the economic quality of reserve (q) gives also an idea of
how fast the reserve volume will produce.

For a given reserve, if we drill more wells the reserve will be
depleted faster, increasing the present value of revenues
number of wells  higher q  higher V
 However, higher number of wells  higher development cost D
 Higher

For the equation NPV = q P B - D, there is a trade off between q
and D, when selecting the system capacity (number of wells, the
platform process capacity, pipeline diameter, etc.)
 For the
alternative “j” with n wells, we get NPVj = qj P B - Dj
 Hence, an important investment decision is:
 How select the best one from a set of mutually exclusive alternatives?
Or, What is the best intensity of investment for a specific oilfield?
 I follow the paper of Dixit (1993), but considering finite-lived options.
The Best Alternative at Expiration (Now or Never)

The chart below presents the “now-or-never” case for three
alternatives. In this case, the NPV rule holds (choose the higher one).


Alternatives: A1(D1, q1); A2(D1, q1); A3(D3, q3), with D1 < D2 < D3 and q1 < q2 < q3
Hence, the best alternative depends on the oil price P. However, P is uncertain!
The Best Alternative Before the Expiration

Imagine that we have t years before the expiration and in
addition the long-run oil prices follow the geometric Brownian

We can calculate the option curves for the three alternatives, drawing
only the upper real option curve (in this case A2), as presented below.

The decision rule is:

If P < P*2 , “wait and see”


Alone, A1 can be even deep-in-the-money,
but wait for A2 is more valuable
If P = P*2 , invest now with A2
 Wait

is not more valuable
If P > P*2 , invest now with the higher
NPV alternative (A2 or A3 )
 Depending

of P, exercise A2 or A3
How about the decision rule along
the time? (thresholds curve)

Let us see a software from PRAVAP-14
Threshold Curves for Three Alternatives
 There
are regions of wait and see and others that the
immediate investment is optimal for each alternative
Investments
D3 > D2 > D1
E&P Process and Options
Oil/Gas Success
Probability = p
 Drill
Expected Volume
of Reserves = B

Revised
Volume = B’
the wildcat? Wait? Extend?
Revelation, option-game: waiting incentives

Appraisal phase: delineation of reserves
 Technical uncertainty: sequential options

Delineated but Undeveloped Reserves.
 Develop? Wait and See? Extend the
option? Invest in additional information?

Developed Reserves.
 Expand the production?
 Stop Temporally? Abandon?
Option to Expand the Production
 Analyzing
a large ultra-deepwater project in Campos
Basin, Brazil, we faced two problems:

Remaining technical uncertainty of reservoirs is still important.
 In
this specific case, the best way to solve the uncertainty is not by drilling
additional appraisal wells. It’s better see the initial production profile.

In the preliminary development plan, some wells presented both
reservoir risk and small NPV.
Some
wells with small positive NPV (are not “deep-in-the-money”)
Depending of the information from the initial production, some wells
could be not necessary or could be placed at the wrong location.
 Solution:


leave these wells as optional wells
Buy flexibility with an additional investment in the production
system: platform with capacity to expand (free area and load)
It permits a fast and low cost future integration of these wells
 The
exercise of the option to drill the additional wells will depend of both
market (oil prices, rig costs) and the production profile response
Modeling the Option to Expand
 Define
the quantity of wells “deep-in-the-money” to start
the basic investment in development
 Define the maximum number of optional wells
 Define the timing (accumulated production) that reservoir
information will be revealed and the revelation distributions
 Define for each revealed scenario the marginal production
of each optional well as function of time.

Consider the secondary depletion if we wait after learn about reservoir
 Add
market uncertainty (stochastic process for oil prices)
 Combine uncertainties using Monte Carlo simulation
 Use an optimization method to consider the earlier exercise
of the option to drill the wells, and calculate option value


Monte Carlo for American options is a growing research area
Many Petrobras-PUC projects use Monte Carlo for American options
Secondary Depletion Effect: A Complication

With the main area production, occurs a slow oil migration from
the optional wells areas toward the depleted main area
optional wells
oil migration
(secondary depletion)
petroleum reservoir (top view) and the grid of wells

It is like an additional opportunity cost to delay the exercise of the option to
expand. So, the effect of secondary depletion is like the effect of dividend yield
Oilfield Development with Option to Expand
 The
timeline below represents a case analyzed in PUC-Rio
project, with time to build of 3 years and information
revelation with 1 year of accumulated prodution
 The
practical “now-or-never” is because many times the
effect of secondary depletion is relevant

The oil migrates from the original area so that the exercise of the
option gradually become less probable (decreasing NPV)
 In
addition, distant exercise of the option has small present value
 Recall the expenses to embed flexibility occur between t = 0 and t = 3
Conclusões
 Os
modelos de opções reais em petróleo trazem uma
metodologia rica para avaliar o investimento ótimo sob
incertezas e valorar as flexibilidades gerenciais

O tradicional fluxo de caixa descontado é muito limitado e
pode induzir a erros sérios em negociações e decisões
 Nós
vimos o modelo clássico, trabalhando com a intuição e
com parte da “caixa de ferramentas” das opções reais

Vimos diferentes processos estocásticos e outros modelos
 Apresentei
uma idéia geral das pesquisas de opções reais na
Petrobras e na PUC-Rio
 Foram mostrados modelos de valor da informação com
simulação combinando incertezas técnicas e de mercado

A metodologia usando distribuições de revelações é prática e dá os
incentivos corretos para o investimento em informação
 Muito
obrigado pelo seu tempo!
Anexos
APPENDIX
SUPPORT SLIDES

See more on real options in the first website on real options at:
http://www.puc-rio.br/marco.ind/
When Real Options Are Valuable?
 Flexibility

(real options) value greatest when:
High uncertainty about the future

Very likely to receive relevant new information over time.
 Information can be costly (investment in information) or free .

High room for managerial flexibility
Allows
management to respond appropriately to this new information
(eg., better fitted development investment; to expand or to contract the
project; etc.)

Projects with NPV around zero
Flexibility
to change course is more likely to be used and therefore is
more valuable
The next chart, real options value (F) versus the oil price (P),
illustrates this point for the option to wait

“Under these conditions, the difference between real options
analysis and other decision tools is substantial” Tom Copeland
Estimating the Model Parameters
 How
to estimate the value of underlying asset V?
 Transactions
in the developed reserves market (USA)

v = value of one barrel of developed reserve (stochastic);
 V = v B where B is the reserve volume (number of barrels);
 v is ~ proportional to petroleum prices P, that is, v = q P ;
 For q = 1/3 we have the “one-third rule of thumb”;
 Let us call q = economic quality of the developed reserve
– The developed reserve value V is an increasing function of q
 Discounted
cash flow estimate of V, that is:
NPV = V - D  V = NPV + D
 It is possible to work with the entire cash-flows, but we can
simplify this job identifying the main sources of value for V
 For fiscal regime of concessions the chart NPV x P is a
straight line, so that we can assume that V is proportional to P
 Let us write the value V = q P B or NPV = q P B - D

Geometric Brownian Motion Simulation

The real simulation of a GBM uses the real drift a. The price P
at future time (t + 1), given the current value Pt is given by:
Pt+1 = Pt exp{ (a - 0.5 s2) Dt + s N(0, 1) Dt }


The risk-neutral simulation of a GBM uses the risk-neutral
drift a’ = r - d . Why? Because by supressing a risk-premium
from the real drift a we get r - d. Proof:




But for a derivative F(P) like the real option to develop an oilfiled,
we need the risk-neutral simulation (assume the market is complete)
Total return r = r + p (where p is the risk-premium, given by CAPM)
But total return is also capital gain rate plus dividend yield: r = a + d
Hence, a + d = r + p  a - p = r - d
So, we use the risk-neutral equation below to simulate P
Pt+1 = Pt exp{ (r - d - 0.5 s2) Dt + s N(0, 1) Dt }
The Options and Payoffs for Both Periods
Using Mean-Reversion with Jumps
Period
t = 0 to T1:
T I M E
First Period
T1: First
Expiration
T1 to T2:
Second Period
T2: Second
Expiration
Options Charts
Comparing Jump-Reversion with GBM


Jump-reversion points lower thresholds for longer maturity
The threshold discontinuity near of T2 is due the behavior of d, that
can be negative for lower values of P: d = r - h( P - P)

A necessary condition for early exercise of American option is d > 0
Technical Uncertainty and Risk Reduction
 Technical
uncertainty decreases when efficient investments
in information are performed (learning process).
 Suppose a new basin with large geological uncertainty. It is
reduced by the exploratory investment of the whole industry

The “cone of uncertainty” (Amram & Kulatilaka) can be adapted to
understand the technical uncertainty:
Expected
Value
confidence
interval
Higher
Risk
Current
project
evaluation
(t=0)
Lower
Risk
Lack of Knowledge Trunk of Cone
Risk reduction by the
investment in information
of all firms in the basin
(driver is the investment, not
directly by the passage of time)
Expected
Value
Project
evaluation
with additional
information
(t = T)
Technical Uncertainty and Revelation

The consequence of an investment in information project are:

Risk reduction process (learning) towards the truth (revelation process)
and revision of expectations leading a revision of decisions.
E[V]
lack of knowledge trunk of cone illustrates these issues
confidence interval
 The
Current project
value (t=0)
Value with
good revelation
Lack of Knowledge Trunk of Cone
Value with
neutral revelation
Value with
bad revelation
Investment in
Information
Project value
after new information
Oil Drilling Bayesian Game (Dias, 1997)


Oil exploration: with two or few oil companies exploring a
basin, can be important to consider the waiting game of drilling
Two companies X and Y with neighbor tracts and correlated oil
prospects: drilling reveal information

If Y drills and the oilfield is discovered, the success probability for X’s
prospect increases dramatically. If Y drilling gets a dry hole, this information
is also valuable for X.

In this case the effect of the competitor presence is to increase the
value of waiting to invest
Company X tract
Company Y tract
Two Sequential Learning: Schematic Tree

Two sequential investment in information (wells “B” and “C”):
Invest
Well “B”
Invest
Well “C”
Posterior
Scenarios
NPV
{
400
300
350 (with 25% chances)
300
{
300
200
250 (with 50% chances)
100
150 (with 25% chances)
- 200
{

Revelation
Scenarios
200
100
The upper branch means good news, whereas the lower one means bad news
Distribuição de Revelações e os Experts

Esse é um procedimento prático de conseguir do técnico expert os
dados para valorar um investimento em informação, perguntando:
 Qual a incerteza total de cada parâmetro técnico relevante? Ou seja,
quais são os parâmetros das distribuições de probabilidades a priori ?
Pela proposição 1, a variância da distribuição a priori é a variância
limite para a distribuição de revelações num processo de aprendizagem
Pela proposição 2, a distribuição de revelações gerada pela nova
informação tem a mesma média da distribuição a priori.
 Para cada alternativa de investimento em informação, qual é a
(%) redução de variância esperada em cada parâmetro técnico?
Pela
proposição 3, essa é também variância da distribuição de revelações

Isso é o mínimo que se precisa saber ao propor investir em informação
 Now considere again the simple equation NPV = V - D = q B P - D



We’ll combine technical uncertainties on q and B with oil price (P) uncertainty
After an information revelation, assume that the optimal capacity choice is
function only of the reserve volume: D(B) = Fixed Cost + Variable Cost x B
The capacity constrain makes E[q B] < E[q] E[B] . The factor g corrects it.
Real Options Evaluation by Simulation + Threshold Curve

Before the information revelation, V/D changes due the oil prices P (recall
= qPB and NPV = V – D). With revelation on q and B, the value V jumps.
V
A
B
Present Value (t = 0)
F(t = 0) =
= F(t=5.5) * exp (- r*t)
Option F(t = 5.5) = V - D
F(t = 8) = 0
Expires Worthless
Visual FAQ’s on Real Options: 9
 Is
possible real options theory to recommend
investment in a negative NPV project?
Answer:
yes, mainly sequential options with
investment revealing new informations

Example: exploratory oil prospect (Dias 1997)
Suppose
a “now or never” option to drill a wildcat
Static NPV is negative and traditional theory recommends to
give up the rights on the tract
Real options will recommend to start the sequential investment,
and depending of the information revealed, go ahead (exercise
more options) or stop
Sequential Options (Dias, 1997)
“Compact Decision-Tree”
Note: in million US$
( Developed Reserves Value )
( Appraisal Investment: 3 wells )
( Development Investment )
( Wildcat
Investment )

EMV = - 15 + [20% x (400 - 50 - 300)]
 EMV = - 5 MM$
Traditional method, looking only expected values, undervaluate
the prospect (EMV = - 5 MM US$):


There are sequential options, not sequential obligations;
There are uncertainties, not a single scenario.
Sequential Options and Uncertainty

Suppose that each appraisal
well reveal 2 scenarios (good
and bad news)
 development option will not be
exercised by rational managers
 option to continue the
appraisal phase will not be
exercised by rational managers
Option to Abandon the Project

Assume it is a “now or
never” option

If we get continuous bad
news, is better to stop
investment
 Sequential options turns
the EMV to a positive
value

The EMV gain is
3.25 - (- 5) = $ 8.25 being:
$ 2.25 stopping development
$6
stopping appraisal
$ 8.25 total EMV gain
(Values in millions)
Economic Quality of the Developed Reserve
 Imagine
that you want to buy 100 million barrels of developed
oil reserves. Suppose a long run oil price is 20 US$/bbl.

How much you shall pay for the barrel of developed reserve?
 One
reserve in the same country, water depth, oil quality,
OPEX, etc., is more valuable than other if is possible to extract
faster (higher productivity index, higher quantity of wells)
 A reserve
located in a country with lower fiscal charge and
lower risk, is more valuable (eg., USA x Angola)
 As higher is the percentual value for the reserve barrel in
relation to the barrel oil price (on the surface), higher is the
economic quality: value of one barrel of reserve = v = q . P

Where q = economic quality of the developed reserve
 The value of the developed reserve is v times the reserve size (B)
Mean-Reversion + Jumps for Oil Prices
 Adopted
in the Marlim Project Finance (equity
modeling) a mean-reverting process with jumps:
where:
(the probability of jumps)
 The
jump size/direction
are random: f ~ 2N
 In case of jump-up, prices
are expected to double

OBS: E(f)up = ln2 = 0.6931
 In case of jump-down, prices
are expected to halve

OBS: ln(½) = - ln2 = - 0.6931
(jump size)
Equation for Mean-Reversion + Jumps
 The
interpretation of the jump-reversion equation is:
continuous (diffusion) process
variation of the
stochastic variable
for time interval dt
discrete
process
(jumps)
uncertainty from
the continuous-time
process (reversion)
mean-reversion drift:
positive drift if P < P
negative drift if P > P
uncertainty from
the discrete-time
process (jumps)
Example in E&P with the Options Lens
 In
a negotiation, important mistakes can be done if we
don´t consider the relevant options
 Consider two
marginal oilfields, with 100 million bbl, both
non-developed and both with NPV = - 3 millions in the
current market conditions

The oilfield A has a time to expiration for the rights of only 6
months, while for the oilfield B this time is of 3 years
 Cia
X offers US 1 million for the rights of each oilfield.
Do you accept the offer?
 With the static NPV, these fields have no value and even
worse, we cannot see differences between these two fields


It is intuitive that these rights have value due the uncertainty and the
option to wait for better conditions. Today the NPV is negative, but
there are probabilities for the NPV become positive in the future
In addition, the field B is more valuable (higher option) than the field A