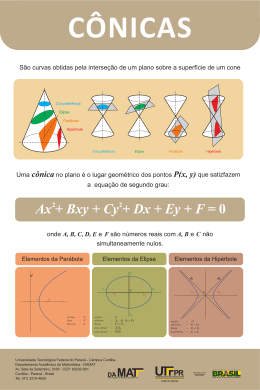
Curso de Geometria Analítica
Abrangência: Graduação em Engenharia e Matemática - Professor Responsável: Anastassios H. Kambourakis
Resumo Teórico 03 - Cônicas- Circunferência, Elipse, Hipérbole e Parábola
INTRODUÇÃO
Cônicas são figuras curvas que podem ser obtidas de diferentes formas, entre elas através da
intersecção de um plano com uma superfície de revolução, como por exemplo um cone.
Circunferência
Hipérbole
Elipse
Parábola
As propriedades destas curvas podem ser estudadas sob o aspecto geométrico e através de um
processo algébrico podemos obter as equações que representam cada uma destas curvas.
CIRCUNFERÊNCIA:
Dado um ponto C e um número real r>0, definimos circunferência de centro C e raio r, ao Lugar
Geométrico dos pontos P do plano que distam r do ponto C, ou ainda, dos pontos P do plano que
eqüidistam de r do ponto C. Isto é, DPC = r .
Se representarmos os pontos P=(x,y) e C=(a,b) pelas suas coordenadas e considerando a fórmula da
distância entre os pontos P e C, então a relação DPC = r pode ser escrita de seguinte forma:
DPC=
√ (x - a )2 + (y - b ) 2 = r
ou
(x - a )2 + (y - b ) 2 = r2
Esta equação recebe o nome de Equação reduzida da Circunferência, pois a mesma representa
todos os pontos P=(x,y) do plano que tem a distância igual a r do ponto (centro) C=(a,b).
Se desenvolvermos esta equação obtemos a Equação Geral da Circunferência como segue:
x2 + y2 –2ax –2by + (a2 + b2 –r2) =0
Particularmente, para determinar a equação de uma circunferência, conhecendo 3 de seus pontos,
basta resolver um sistema de 3 equações resultantes à aplicação de cada ponto na equação da
circunferência em sua forma geral.
Posições relativas entre pontos e Circunferências:
Considerando o Ponto P = (x0,y0) e a circunferência de centro C=(a,b) e Raio r, teremos:
i. P pertence à Circunferência se a distância entre o Ponto e o centro da circunferência for igual
ao Raio, isto é
√ (x0 - a )2 + (y0 - b ) 2 = r;
r
C•
•
P
ii.
P é interno à Circunferência se a distancia entre o Ponto e o centro da circunferência for menor
do que o Raio, isto é
√ (x0 - a )2 + (y0 - b ) 2 < r;
r
C•
iii.
•
P
P é externo à Circunferência se a distancia entre o Ponto e o centro da circunferência for maior
do que o Raio, isto é
√ (x0 - a )2 + (y0 - b ) 2 > r.
r
C•
•
P
Posições relativas entre retas e Circunferências:
Considerando a reta ax + by + c =0 a circunferência de centro C=(x0,y0) e Raio r, teremos:
i. A reta é tangente à circunferência se a distância entre o Centro da circunferência e a reta for
igual ao raio, isto é:
|ax0 + by0 + c |
 = r;
√ a2 + b2
r
C•
•
Observamos que neste caso existe um ponto comum entre a reta e a circunferência que é obtido pela
solução do sistema das duas equações.
ii.
A reta é secante à circunferência se a distância entre o Centro da circunferência e a reta for
menor do que o raio, isto é:
|ax0 + by0 + c |
 < r;
√ a2 + b2
r
•
C•
•
•
Observamos que neste caso existem dois pontos comuns entre a reta e a circunferência que são
obtidos pela solução do sistema das duas equações.
iii. A reta é externa à circunferência se a distância entre o Centro da circunferência e a reta for
maior do que o raio, isto é:
|ax0 + by0 + c |
 > r;
√ a2 + b2
r
C•
Observamos que neste caso não existem pontos comuns entre a reta e a circunferência.
Posições relativas entre Circunferências:
Considerando duas Circunferências de Centro C1=(a1,b1) e raio r1 e de Centro C2=(a2,b2) e raio r2 ,
respectivamente, teremos:
i. As circunferências são tangentes, externa ou internamente e teremos que a distância entre os
centros será para cada caso:
r1
C1•
r1
•
r2
•C2
DC1C2 = r1+ r2
C1•
r2
•C2
DC1C2 = | r1- r2|
Observamos que neste caso existe um ponto comum entre as circunferências que é obtido pela
solução do sistema das duas equações.
ii. As circunferências são externa ou internamente sem pontos comuns e teremos que a distância
entre os centros será para cada caso:
r1
C1•
r1
r2
•C2
DC1C2 > r1+ r2
C1•
r2 •C2
DC1C2 < | r1- r2|
Observamos que neste caso não existem pontos comuns entre as circunferências.
iii.
As circunferências são secantes e teremos que a distância entre os centros será:
r1
C1•
r2
•C2
DC1C2 < r1+ r2
e
DC1C2 > | r1- r2|
Observamos que neste caso existem dois pontos
comuns entre as circunferências que são obtidos
pela solução do sistema das duas equações.
ELIPSE:
Definimos Elipse ao Lugar Geométrico dos pontos P do plano, cuja soma das distâncias de dois
pontos fixos F1 e F2 (focos), é igual a um valor real constante 2a, com a≠0, Isto é:
P F1 + P F2 = 2a
Desta forma teremos:
B1
A1
•
F1
•P
•
•
C
Adotaremos as seguintes notações:
F1 F2 = Distância Focal da elipse = 2c;
♦ A1 A2 = Eixo Maior da elipse = 2a;
♦ B1 B2 = Eixo Menor da elipse = 2b;
♦ C = Centro da elipse;
♦ P = Ponto genérico(qualquer) da elipse;
♦ F1C = F2C = c = Semi distância focal;
♦ A1C = A2C =a = Semi eixo maior;
♦ B1C = B2C =b = Semi eixo menor;
♦
F2
A2
B2
Considerando que B1F1+ B1F2 = 2a, teremos que B1F1 =a, assim o triângulo F1CB1, que é reto em
C, tem como catetos CF1=c e CB1=b e como hipotenusa B1F1=a, o que nos permite obter a seguinte
relação, entre o eixo maior, o eixo menor e a distância focal de uma Elipse:
a2 = b2 + c2
Observamos que a relação entre a semi-distância focal e o semi-eixo maior, é um número real que
chamamos de excentricidade (ε) da Elipse e nos permite avaliar o quanto ma elipse é excêntrica em
relação a uma circunferência, assim teremos:
c
ε = 
Avaliando esta relação podemos afirmar que 0<ε<1.
a
Quando ε tende a 0(c=0), a elipse tende a ser uma circunferência;
Quando ε tende a 1 (a=c), a elipse tende a ser um conjunto de duas retas coincidentes;
Quando mais próximo de 1 estiver o valor de ε , mais excêntrica será a Elipse.
Equação Geral da Elipse:
Ao representarmos os elementos da elipse no plano cartesiano, pelas suas coordenadas cartesianas e
aplicando a definição da Elipse teremos que PF1 + PF2 = 2a;
Sendo P=(x,y), F1=(x F1,y F1) e F2=(x F2,y F2), teremos:
F2
yF2
yP
yC
yF1
0
√(x-x F1)2 + (y-yF1) 2
C
P
F1
xF1 xC xF2 xP
+
√(x-xF2)2 + (y-yF2) 2
= 2a
Considerando que esta equação tem como incógnitas
apenas os valores de x e y (coordenadas do ponto P,
ao resolver esta equação irracional chegaremos a uma
equação de segundo grau de duas variáveis do tipo :
Ax2 + By2 + Cxy + Dx + Ey + F = 0
[com A, B, C, D, E e F ∈ IR (reais)]
Esta equação representa a Equação Geral de uma Elipse no plano.
Observamos que embora a Elipse seja representada por equação de segundo grau com duas
variáveis, nem toda equação de segundo grau com duas variáveis representa uma Elipse.
Equação Reduzida da Elipse:
Se representarmos a mesma Elipse em uma posição espacial no Plano Cartesiano, com centro na
Origem e focos no eixo das abscissas, embora sua posição seja diferente, seus elementos tais como,
eixos, distância focal, excentricidade etc, permanecem os mesmos.
Desta forma podemos determinar uma equação mais simples para representar elipses com os
mesmos elementos, assim yF1 = yF2 = 0 e xC= yC= 0, então a relação PF1 + PF2 = 2a resulta em:
√(x-x F1)2 + (y-0) 2
+
√(x-xF2)2 + (y-0) 2
= 2a
ou
√(x-x F1)2 + y 2
xC
xF1
√(x-xF2)2 + y 2
= 2a
Considerando ainda que a2 = b2 + c2
ao resolver esta equação irracional chegaremos a uma
equação do tipo:
P
yP
+
xP xF2
y2
x2
 +  =1
a2
b2
sendo a e b os semi-eixos da Elipse.
Esta equação representa a Equação Reduzida de uma Elipse no plano.
Observamos que embora a esta equação representa uma Elipse em posição especial, com centro na
origem e Focos sobre o eixo das abscissas, poderá certamente, em termos de investigação de
propriedades e cálculos, representar qualquer elipse do plano que tem os mesmos elementos (eixos,
distância focal, excentricidade etc).
A equação Reduzida de uma Elipse pode ser representada em outras formas dependendo a posição
especial que ocupa no Plano Cartesiano assim teremos:
F1
F1
•
•
C
• F2
•
x2
y2
 +  = 1
b2
a2
(x-xC)2 (y-yC)2
 +  = 1
a2
b2
yC
F1
•
•
•
C
• F2
C
• F2
y2
x2
 +  = 1
a2
b2
(y-yC)2
(x-xC)2
 +  = 1
a2
b2
F1
yC
•
•
C
• F2
xC
xC
HIPÉRBOLE:
Definimos Hipérbole ao Lugar Geométrico dos pontos P do plano, cuja diferença, em módulo, das
distâncias de dois pontos fixos F1 e F2 (focos),é igual a um valor real constante 2a, com a≠0, Isto é:
| P F1 - P F2 | = 2a
Desta forma teremos:
B1 •
•
F1
•
•
A1
•
C
A2•
Adotaremos as seguintes notações:
♦ F1 F2 = Distância Focal da Hipérbole = 2c;
♦ A1 A2 = Eixo Real da Hipérbole = 2a;
♦ B1 B2 = Eixo Virtual da Hipérbole = 2b;
♦ C = Centro da Hipérbole;
♦ P = Ponto genérico(qualquer) da Hipérbole;
♦ F1C = F2C = c = Semi distância focal;
♦ A1C = A2C =a = Semi eixo real;
♦ B1C = B2C =b = Semi eixo virtual;
P
•F2
•B2
Considerando o triângulo A1CB1, que é reto em C, tem como catetos CA1=a e CB1=b e como
hipotenusa A1B1=a, o que nos permite obter a seguinte relação, entre o eixo maior, o eixo menor e a
distância focal de uma Hipérbole:
c2 = a2 + b2
Observamos que a relação entre a semi-distância focal e o semi-eixo maior, é um número real que
chamamos de excentricidade (ε) da Hipérbole e nos permite avaliar o quanto uma Hipérbole é
excêntrica, assim teremos:
c
Avaliando esta relação podemos afirmar que ε>1.
ε = 
Quando maior for o valor de ε , mais excêntrica será a Hipérbole.
a
Equação Geral da Hipérbole:
Ao representarmos os elementos da Hipérbole no plano cartesiano, pelas suas coordenadas
cartesianas e aplicando a definição da Hipérbole teremos que |PF1 - PF2 | = 2a;
Sendo P=(x,y), F1=(x F1,y F1) e F2=(x F2,y F2), teremos:
F2
yF2
yP
yC
yF1
0
|
C
√(x-x F1)2 + (y-yF1) 2 - √(x-xF2)2 + (y-yF2) 2
|= 2a
P
F1
xF1 xC xF2 xP
Considerando que esta equação tem como incógnitas
apenas os valores de x e y (coordenadas do ponto P,
ao resolver esta equação irracional chegaremos a uma
equação de segundo grau de duas variáveis do tipo :
Ax2 + By2 + Cxy + Dx + Ey + F = 0
[com A, B, C, D, E e F ∈ IR (reais)]
Esta equação representa a Equação Geral de uma Hipérbole no plano.
Observamos que, estruturalmente as Equações da Elipse e da Hipérbole tem a mesma equação geral
e que embora a Hipérbole seja representada por equação de segundo grau com duas variáveis, nem
toda equação de segundo grau com duas variáveis representa uma Hipérbole.
Equação Reduzida da Hipérbole:
Se representarmos a mesma Hipérbole em uma posição espacial no Plano Cartesiano, com centro na
Origem e focos no eixo das abscissas, embora sua posição seja diferente, seus elementos tais como,
eixos, distância focal, excentricidade etc, permanecem os mesmos.
Desta forma podemos determinar uma equação mais simples para representar Hipérboles com os
mesmos elementos, assim yF1 = yF2 = 0 e xC= yC= 0, então a relação |PF1 - PF2|= 2a resulta em:
| √(x-x F1)2 + (y-0) 2 - √(x-xF2)2 + (y-0) 2 |
ou
xC
xF1
+
√(x-xF2)2 + y 2 | = 2a
Considerando ainda que c2 = a2 + b2
ao resolver esta equação irracional chegaremos a uma
equação do tipo:
P
yP
| √(x-x F1)2 + y 2
= 2a
xP xF2
x2
y2
 −  =1
b2
a2
sendo a e b os semi-eixos da Hipérbole.
Esta equação representa a Equação Reduzida de uma Hipérbole no plano.
Observamos que embora a esta equação representa uma Hipérbole em posição especial, com centro
na origem e Focos sobre o eixo das abscissas, poderá certamente, em termos de investigação de
propriedades e cálculos, representar qualquer Hipérbole do plano que tem os mesmos elementos
(eixos, distância focal, excentricidade etc).
A equação Reduzida de uma Hipérbole pode ser representada em outras formas dependendo a
posição especial que ocupa no Plano Cartesiano assim teremos:
F1
F1
•
•
C
• F2
•
x2
y2
 −  = 1
b2
a2
(x-xC)2 (y-yC)2
 −  = 1
a2
b2
yC
F1
•
•
•
C
• F2
C
• F2
y2
x2
 −  = 1
a2
b2
(y-yC)2
(x-xC)2
 −  = 1
a2
b2
F1
yC
•
•
C
• F2
xC
xC
PARÁBOLA:
Definimos Parábola ao Lugar Geométrico dos pontos P do plano, que eqüidistam. isto é, tem a
mesma distância de um ponto fixo F (foco) e de uma reta fixa d (diretriz).
e
Desta forma teremos:
PF = Pd
Adotaremos as seguintes notações:
Ponto F = Foco da Parábola;
♦ Ponto V = Vértice da Parábola;
♦ Reta d = Diretriz Parábola;
♦ Reta e = Eixo Parábola;
♦ FD = p = Parâmetro da Parábola
p
♦ FV =VD = /2 = Semi-Parâmetro da Parábola;
♦ Ponto P = Ponto genérico(qualquer) da Parábola;
♦ PF= Distância do Foco ao ponto P;
♦ Pd= Distância do ponto P à reta diretriz d;
♦
P•
PF
•
Pd
F
V
p
d
D
Equação Geral da Parábola:
Ao representarmos os elementos da Parábola no plano cartesiano, pelas suas coordenadas
cartesianas e aplicando a definição da Parábola teremos que PF = Pd;
yF
Sendo P=(x,y), F=(x F,y F) e d=ax+by+c =0, teremos:
|ax+by +c |
F
√(x-x F)2 + (y-yF) 2
yP
√a2 + b2
P
d
0
xF1 xC xF xP
= 
Considerando que esta equação tem como incógnitas
apenas os valores de x e y (coordenadas do ponto P),
ao resolver esta equação irracional chegaremos a uma
equação de segundo grau de duas variáveis do tipo :
Ax2 + By2 + Cxy + Dx + Ey + F = 0
[com A, B, C, D, E e F ∈ IR (reais)]
Esta equação representa a Equação Geral de uma Parábola no plano.
Observamos que, estruturalmente as Equações da Elipse, da Hipérbole e da Parábola tem a mesma
equação geral e que embora a Parábola seja representada por uma equação de segundo grau com
duas variáveis, nem toda equação de segundo grau com duas variáveis representa uma Parábola.
Equação Reduzida da Parábola:
Se representarmos a mesma Parábola em uma posição espacial no Plano Cartesiano, com Vértice na
Origem e foco no eixo das ordenadas, embora sua posição seja diferente, seus elementos
permanecem os mesmos. Desta forma podemos determinar uma equação mais simples para
representar Parábolas com os mesmos elementos, assim xF = 0, yF= p/2 e a reta d tem equação y=p/2 (0x+y+ p/2=0, com a=0, b=1 e c= p/2) , então a relação
PF = Pd resulta em:
√(x2 + (y- p/2) 2
F
P
V
| 0x + y + p/2|
= 
1
ao resolver esta equação irracional chegaremos a uma
equação do tipo:
x2 =2py
sendo p o Parâmetro da Parábola.
Esta equação representa a Equação Reduzida de uma Parábola no plano.
Observamos que embora a esta equação representa uma Parábola em posição especial, com Vértice
na origem e Foco sobre o eixo das ordenadas, poderá certamente, em termos de investigação de
propriedades e cálculos, representar qualquer Parábola do plano que tem os mesmos elementos .
A equação Reduzida de uma Parábola pode ser representada em outras formas dependendo a posição
especial que ocupa no Plano Cartesiano assim teremos:
F
d
•
•
V
V
•
d
•F
x2= 2py
•
V
•
x2= −2py
F
•
d
F
•
V
d
y2= 2px
y2= −2px
Diretrizes da Elipse e Hipérbole:
Vimos que a Diretriz é parte integrante da definição de uma Parábola.
As Elipses e Hipérboles tem também definidas suas diretrizes como retas perpendiculares,
respectivamente, aos eixos Maior e Real a uma distância do Centro igual ao valor de
a
/ε , sendo a o
semi-eixo (maior ou real) e ε a excentricidade da Elipse ou Hipérbole, conforme o caso. Considerando
c
a
que ε = /a , podemos assumir que /ε = a2/c.
Representando no plano cartesiano teremos.
d2
d1
Onde d1 e d2 são as diretrizes da Elipse
a
/ε = a2/c
a
a
/ε = a2/c
2( /ε )= 2(a2/c)
d1
d2
a
Onde d1 e d2 são as diretrizes da Hipérbole
a
/ε = a2/c
/ε = a2/c
a
2( /ε )= 2(a2/c)
Observamos que as Diretrizes de qualquer cônica (Elipse, Hipérbole, Parábola), desempenham um
papel especial para as mesmas e que por serem relacionadas com a excentricidade, sua posição em
relação ao centro (origem) determina, propriamente seu tipo e espécie.
Retângulo de Referência e Assíntotas da Hipérbole:
Os Eixos Real (2a) e Virtual (2b) da Hipérbole são lados de um retângulo que, em função da relação
c2 = a2 + b2, determina a qualidade da Hipérbole, recebendo por isso a denominação de “Retângulo
de Referência” da Hipérbole. As diagonais deste retângulo são duas retas chamadas “Assíntotas”
da Hipérbole. Representando no plano cartesiano teremos:
Assíntotas
Observamos que as Assíntotas são retas que
contem o centro da Hipérbole e os pontos de
coordenadas (a,b), considerando, os valores
positivos e/ou negativos, conforme a posição.
Retângulo de referência
Cônicas: Relações complementares
| PF1 ± PF2 |= 2a
D2
D1
y
P
x
F1
F2
y2
x2
|√(x-x F1)2 + y 2 ± √(x-xF2)2 + y 2 | = 2a
 ±  =1
a2
b2
Se definirmos a distância de um ponto P ao Foco por r (raio vetor)
Considerando que PF1 = r1 e PF2 = r2 , sendo D1 e D2 as Diretrizes
teremos, também as seguintes relações:
r1 = a + ε x e r2 = a − ε x ,
D1
y
F1
a2 = b2+ c2
D2
para a Elipse.
, 2a= eixo Maior, 2b= eixo Menor e 2c= dist. Focal
P
x
F2
r1 = ε x + a e r2 = ε x − a ,
c2 = a2+ b2,
para a Hipérbole.
2a= eixo Real e 2b= eixo Virtual e 2c= dist. Focal
Definição geral de uma Cônica:
Através do(s) Foco(s) e da(s) Diretriz(es), podemos enunciar uma definição Geral para as Cônicas,
como segue:
Dados um ponto F (foco) e uma reta d (diretriz), definimos como sendo uma Cônica, ao Lugar
Geométrico dos pontos P do plano tais que PF = k• Pd.
Sendo:
• PF a distância do Ponto P ao Foco F;
• Pd a distância do ponto P à diretriz d;
• k um número real maior que zero.
Conforme os valores assumidos por k, teremos:
•
•
•
Para 0< k < 1, a Cônica será uma Elipse;
Para k >1 , a Cônica será uma Hipérbole;
Para k = 1, a Cônica será uma Parábola.
Identificação de uma Cônica através de sua equação Geral
Considerando a Equação Ax2 + By2 + Cxy + Dx + Ey + F = 0, com A, B, C, D, E e F ∈ IR (reais),
sabemos que esta equação poderá representar uma Cônica. A identificação desta cônica é possível
através da análise dos valores de A, B, C, D, E, F e os valores de G, H, I, assim determinados:
G=
A
C/2
D/2
C/2
B
E/2
D/2
E/2
A
;
C/2
H=
F
;
C/2
I
=
A + B
B
Teremos então:
G = 0 Î Cônica Falsa.
H = 0 Î Parábola.
H< 0 Î Hipérbole.
G≠0Î
G
H>0Î
•
I<0Î
A = B e C = 0 Î Circunferência.
A ≠B
G
•
ou C ≠ 0 Î Elipse.
I > 0 Î Cônica Falsa.
Determinação da equação reduzida correspondente a uma Cônica
I.
A Cônica foi Identificada como sendo Elipse ou Hipérbole.
Neste caso a Equação reduzida será do tipo: m x2 + n y2 + p =0.
Sendo:
m+n = I
m•n=H
p = G/H
II.
A Cônica foi Identificada como sendo uma Parábola.
Neste caso a Equação reduzida será do tipo: m x2 + n y =0.
Sendo:
m=I
m • n2 = − 4G
ou
n=
√ (−4G/I )
Centro Universitário da FSA
Prof.: Anastassios H.K.