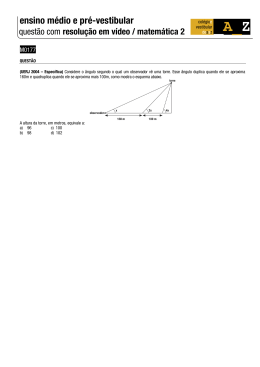
Lista de Exercícios 3 - Gabriel Mendes (1º Ano)
1 - (Unicamp-SP) Uma pessoa de 1,65 m de altura observa o topo de um edifício conforme o
esquema abaixo. Para sabermos a altura do prédio, devemos somar 1,65m a:
(E)
a) b cos a
b) a cos a
c) a sen a
d) b tg a
e) b sen a
2 - (CEFET-PR) Se na figura abaixo AB = 9cm, o segmento DF mede, em cm:
(6cm)
3 - Calcular as medidas dos ângulos internos do triângulo ABC indicado pela figura abaixo:
(2√3)
(2√3)
4 - Nas figuras abaixo, determinar o valor de x
a)
(x = 6) b)
(x = 10√3)
5 - No triângulo retângulo da figura abaixo, determine as medidas de x e y indicadas (Use: sen
65° = 0,91; cos 65° = 0,42 ; tg 65° = 2,14) (y = 3.78 ; x = 8.19)
6 - Considerando o triângulo retângulo ABC da figura, determine as medidas a e b indicadas.(a
= 24 ; b = 12)
7 - Determine o valor de x e y na figura abaixo:
'
(x = 100√3 ; y = 100)
8 - (UFPI) Um avião decola, percorrendo uma trajetória retilínea, formando com o solo, um
ângulo de 30º (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1
000 metros, qual a altura atingida pelo avião? (500m)
9 - (Cefet – PR) A rua Tenório Quadros e a avenida Teófilo Silva, ambas retilíneas, cruzam-se
conforme um ângulo de 30º. O posto de gasolina Estrela do Sul encontra-se na avenida Teófilo
Silva a 4 000 m do citado cruzamento. Portanto, determine em quilômetros, a distância entre o
posto de gasolina Estrela do Sul e a rua Tenório Quadros? (4000√3/3)
10 - Uma escada está apoiada em um muro de 2 m de altura, formando um ângulo de 45º.
Qual é o comprimento da escada?(2√2)]
11 - Em certa hora do dia, os raios do Sol incidem sobre um local plano com uma inclinação de
60° em relação à horizontal. Nesse momento, o comprimento da sombra de uma construção de
6m de altura será igual a quanto? (2√3)
12 - A figura representa um barco atravessando um rio, partindo de A em direção ao ponto B. A
forte correnteza arrasta o barco em direção ao ponto C, segundo um ângulo de 60º. Sendo a
largura do rio de 120 m, a distância percorrida pelo barco até o ponto C, é:
(240m)
13 - Um observador, no ponto O da figura, vê um prédio segundo um ângulo de 75°. Se esse
observador está situado a uma distância de 12m do prédio e a 12m de altura do plano
horizontal que passa pelo pé do prédio, então qual é a altura do prédio, em metros?
(H = 4(3 + √3))
14 - Um turista vê o topo de uma torre construída em um terreno plano, sob um ângulo de 30°.
Aproximando-se da torre mais 374 m, passa a vê-la sob um ângulo de 60°. Considerando que
a base da torre está no mesmo nível do olho do turista, calcule a altura da torre.
(187√3)
15 - (Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano
horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de: (E)
a) 6√3 m.
b) 12 m.
c) 13,6 m.
d) 9√3 m.
e) 18 m.
16 - (UFAM) Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a,
respectivamente, então a tangente do ângulo oposto ao menor lado é: (B)
a) 2√3
b) √3
3
c) √3
6
d) √20
20
e) 3√3
17 - Uma torre de observação é construída em uma região plana. Um bombeiro precisa
determinar aaltura h da torre. Ele observa a torre sob um ângulo de 60°, a partir de um ponto P,
situado a d metrosdesta. Partindo de P, ao se afastar da torre por mais 10 metros, passa a vêla sob um ângulo de 45°.Qual a altura da torre, em metros?
(10√3 / √3 - 1)
18 – Um homem tenta se olhar completamente no espelho, para conseguir isso ele se distancia
do espelho 1 metro. Sabendo que o ângulo de incidência da luz no espelho para que ele veja
os próprios pés é de 30o(î) e que o ângulo de incidência da luz no espelho para que ele veja o
ponto mais alto de sua cabeça é de 2o(î2). (2.0)
Dados: tg 2º= 0.035; sen 2º= 0.034; cos 2º= 0.999; sen 32º= 0.53.
a) Calcule a altura do homem em metros.
b) Calcule a área do triângulo CDO.
19 - No WBC um competidor tentou fazer um “entrechat deux”, um salto no qual ele teria que
saltar e abrir e fechar a perna repetidas vezes, sabendo que ele tem um limite de abertura de
perna igual ao comprimento entre seus ombros, que é de 40 cm e que o comprimento de suas
pernas é de 80 cm. Qual é o ângulo inteiro máximo de abertura da perna desse competidor?
(Dados: sen10o= 0.174; sen11o = 0.191; sen12o= 0.208; sen13o= 0.225; sen14o= 0.242;
sen15o= 0.259; sen16o= 0.276)
20 - Um jogador de futebol está na final da Champions League e tem a chance de vencer no
ultimo minuto do jogo, sofreu um pênalti e vai cobrá-lo, porém está indeciso onde bater. Ele
sabe que se bater do lado direito do goleiro, vai errar. Nos últimos segundos antes de bater, ele
chama o técnico e pergunta qual é o tamanho do goleiro adversário e do tamanho dos braços
do mesmo, tendo como resposta que o tamanho do goleiro é 1.9 metros e que os braços o
fazem ter uns 40 cm extra pra pegar a bola, além disso, o técnico lembrou-lhe que o impulso do
goleiro o faz alcançar mais 30 cm. Sabendo que o gol tem 2.5 metros de altura, 7.5 metros de
comprimento, que a distância entre a marca do pênalti e o gol é de 11 metros, e que o goleiro
defende a bola sempre que essa vier em seu raio de ação e que ele nunca defende quando a
bola vier fora de seu raio de ação. Qual deve ser o ângulo inteiro mínimo e o máximo
(horizontal) chutado no gol para que o batedor seja campeão? (Desenhe a área de atuação do
goleiro na imagem abaixo).
(Dados: tg 11o= 0.194; tg12o= 0.213; tg13o= 0.231; tg14o= 0.249; tg15o= 0.268; tg 16o= 0.287;
tg17o= 0.301; tg 18o= 0.325; tg19o= 0.344)