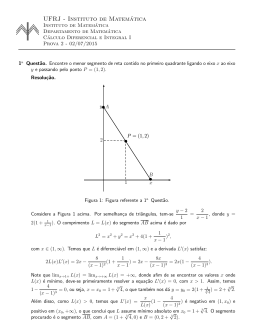
Primeira Avaliação de Estruturas Algébricas 2 - 080020 - A
Professor: Luiz Hartmann
Nome:
RA:
15/04/2013
Questões
01a
02a
03a
04a
Total
Notas
..........................................................................................................
Indique claramente qual questão está sendo respondida em cada folha de resposta utilizada.
Esta prova terá duração de (01) uma hora e (40) quarenta minutos.
Escolha quatro questões das dez abaixo e resolva.
..........................................................................................................
Justifique as suas afirmações. Afirmações sem justificativa não serão consideradas.
Questão 01: Verifique se é verdadeira ou falsa cada afirmação e justifique sua resposta.
(a) Se f : A → B e g : B → C são homomorfismos de anéis, então g ◦ f : A → C é um homomorfismo de
anéis.
(b) Todo anel de integridade finito é corpo.
(c) Sejam A um anel comutativo com unidade e I ideal de A. Então I é maximal se, e somente se, A/I é
corpo.
(d) Existem mais de dois ideais em R.
(e) Seja A = C([0, 1]) o anel das funções reais contı́nuas. Então A é um domı́nio de integridade.
Questão 02: Seja A um domı́nio de integridade e seja ϕ : Z → A definida por ϕ(n) = n1A para todo n ∈ Z.
Mostre que ϕ é um homomorfismo de aneis. E ainda, demonstre que se N (ϕ) 6= {0} então existe um único
p ∈ Z, tal que N (ϕ) = pZ e p é primo.
Questão 03: Mostre que (Z × Z, +, .), onde (a, b) + (c, d) = (a + c, b + d) e (a, b).(c, d) = (ac, ad + bc), é um
anel. É comutativo? Tem unidade? Determine os elementos inversı́veis e os divisores de zero deste anel.
Questão 04: Seja A um anel com unidade tal que x2 = x, para todo x ∈ A. Mostre que A é um anel de
integridade se, e somente se, A ' Z2 .
Questão 05: Mostre que em todo anel comutativo com unidade A 6= {0} existe pelo menos um ideal maximal
M de A.
Questão 06: Determine todos os homomorfismos de Z em Z4 .
Questão 07: Seja A uma anel
√ comutativo com unidade e I um ideal de A. Seja
n
N tal que x ∈ I}. Mostre que I é um ideal de A contendo I.
√
I = {x ∈ A/∃n ∈
Questão 08: Seja F : C([0, 2π]) → R definida por F (f ) = f (π) para toda f ∈ C([0, 2π]). Mostre que F é
um homomorfismo, determine ImF , N (F ), e identifique o anel C([0, 2π])/N (F ).
Questão
09: Seja {Jn }n∈N uma famı́lia de ideais de A. Mostre que se J1 ⊂ J2 ⊂ . . . ⊂ Jn ⊂ . . ., então
S
J = n∈N Jn , é um ideal de A.
Questão 10: Seja A = C([0, 2π]) o anel das funções reais contı́nuas (com as operações usuais de soma e
produto de funções definidas no intervalo [0, 2π]). Prove que, M é um ideal maximal de A se, e somente se,
∃a ∈ [0, 2π] tal que
M = {f ∈ A/f (a) = 0}.
Boa Prova!