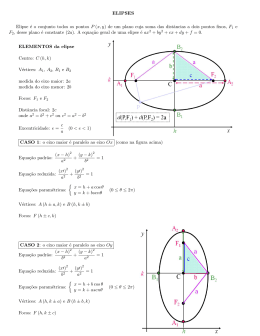
Elementos de Cálculo I - Notas de aula 7
Prof Carlos Alberto Santana Soares
Elipse
Definição 1 Sejam 𝐹1 e 𝐹2 dois pontos no plano. Seja ainda um número 2𝑎 maior que a
distância entre 𝐹1 e 𝐹2 , distância esta que indicaremos por 2𝑐. Chamamos elipse de focos 𝐹1
e 𝐹2 e eixo maior 2𝑎 o conjunto de todos os pontos 𝑃 (𝑥, 𝑦) tais que
𝑃 𝐹1 + 𝑃 𝐹2 = 2𝑎,
ou ainda, distância de 𝑃 a 𝐹1 + distância de 𝑃 a 𝐹2 = 2𝑎.
Abaixo temos representada a eplipse de focos (1, 2) e (−1, −2) e eixo maior 6.
𝑦
..
..........
𝐹 𝑖𝑔𝑢𝑟𝑎7.1
4
𝑃𝐹1 + 𝑃𝐹2 = 6
3..............................................
.....
....
....
.....
....
.....
...
.....
𝐹
1
...
....
.
.
.
.
.
.
.
.
.
.
.
∙
.
.
.
.
.............
.
2
...
..
. .. .
..
..
.. ..........
....
.
.....
...
...
..... ....
....
...
..... .
..
..
.
.
.
..........
..
..
.
....
.
.
.
...........∙
...
.......
...
..... ...
...
...
..... ....
.
..
.
...
.
.
.
.
.
....
..
...
.....
...
..
..
.....
...
..
..
..
..
.....
..
..
..
.....
.
.
.
.
.
.
.
.
...
.
....
..
..
...
.....
..
..
.....
..
...
..
..
.....
...
..
..
.....
.
.
..
.
.
...
.
.
.
.
..
....
...
...
..
.....
..
...
... .......
..
...
... .....
..
...
.
.. .........
.
..
.
.
. .
..
....
...................
..
....
.
...
....
∙.........
....
...
.....
....
.
.
.
.
....
..
.....
.....
......
......
.......
..........
.......................
1
2𝑐
−5 −4 −3 −2 −1
−1
𝑃
1
2
3
4
.....
.
𝑥
.....
5
−2
𝐹2
−3
−4
Problema 2 Como determinar a equação de uma elipse? Em particular, determinemos a
equação da elipse de focos (-1,1) e (1,2) e eixo maior igual a 4.
Um ponto (𝑥, 𝑦) estará na elipse se, e somente se, a soma de suas distâncias aos focos é
igual a 4, isto é, devemos ter,
√
√
(𝑥 + 1)2 + (𝑦 − 1)2 + (𝑥 − 1)2 + (𝑦 − 2)2 = 4.
Dsesenvolvendo, teremos
√
√
√
√
(𝑥 + 1)2 + (𝑦 − 1)2 + (𝑥 − 1)2 + (𝑦 − 2)2 = 4 ⇔ (𝑥 + 1)2 + (𝑦 − 1)2 = 4− (𝑥 − 1)2 + (𝑦 − 2)2
√
√
⇔ ( (𝑥 + 1)2 + (𝑦 − 1)2 )2 = (4 − (𝑥 − 1)2 + (𝑦 − 2)2 )2 ⇔
√
⇔ (𝑥 + 1)2 + (𝑦 − 1)2 = 16 − 8 (𝑥 − 1)2 + (𝑦 − 2)2 + (𝑥 − 1)2 + (𝑦 − 2)2 ⇔
√
⇔ 𝑥2 + 𝑦 2 + 2𝑥 − 2𝑦 + 2 = 16 − 8 (𝑥 − 1)2 + (𝑦 − 2)2 + 𝑥2 + 𝑦 2 − 2𝑥 − 4𝑦 + 5 ⇔
√
√
⇔ −4𝑥−2𝑦+19 = 8 (𝑥 − 1)2 + (𝑦 − 2)2 ⇔ (−4𝑥−2𝑦+19)2 = (8 (𝑥 − 1)2 + (𝑦 − 2)2 )2 ⇔
⇔ 48𝑥2 + 60𝑦 2 − 16𝑥𝑦 + 24𝑥 − 180𝑦 − 41 = 0.
A elipse está representada abaixo.
1
𝑦
...
.... ....
𝐹 𝑖𝑔𝑢𝑟𝑎7.2
4
................................
.................
.........
..........
.......
........
......
.......
.
....
.
.
.
.
....
....
.
.
.
...
..
.
.
...
.
...
...
.
.
...
...
.
∙
...
..
.
.
...
....
....
...
.
....
.
.
.
...
.
.
...
∙
...
...
....
...
...
...
....
.
....
.
.
.
.....
....
.......
......
........
........
............
.........
............................................
3
𝐹2
2
1
𝐹1
−5 −4 −3 −2 −1
−1
1
2
3
4
.....
.
𝑥
.....
5
−2
−3
−4
Observe na figura 7.3 abaixo os lementos aos quais sempre nos referiremos em uma elipse.
Neste caso, os elementos estão identificados na elipse acima.
𝑦
..
..........
𝐹 𝑖𝑔𝑢𝑟𝑎7.3
4
𝐵1 3
.......................................................
...........
.......
.........
......
....... ....
....
......
....
.
.
.
.
.
.
...
..
...
.
.
.
..
.
..
..
.
......∙....
.
.
.
.
.
.
..
...
...
..
.
.
.
.
.
.
.
.
...
..
..
..∙
.
.
...
.
.
.
..
.
.
...
..
..
.. ...........
...
.
.
..
.
.
.
....
.......
..
.
.
.
.
.
.
.
...
..
....
.
.
.
...
.
.
.
.
.
.
..
..
.
...
..
......
...
...
.....∙
..
...
... ...........
..
....
..
.....
∙
....
..
.
....
.
.
.
..
....
.. ............
......
.. .......
.......
.........
....
................. ...........................
.............
𝐴2 𝐹 1
2
𝐶∙
1
𝐹2
−5 −4 −3 −2 −1
𝐵21
−1
𝐴1
2
3
4
.....
..
𝑥
....
5
−2
−3
−4
Temos os elementos:
Focos: F1 e F2
Distância focas: A distãncia entre os focos, indicada por 2c.
Centro: Ponto médio dos segmentos determinados pelos focos
Eixo Maior: Segmento A1A2, cujo comprimentos é igual a 2a.
Eixo Menor: Segmento B1B2, cujo comprimento representaremos por 2b.
Vértices: São os pontos A1, A2, B1, B2.
Excentricidade: Número 𝑒 dado por 𝑒 =
𝑐
𝑎
Vale notar que 𝑎2 = 𝑏2 + 𝑐2 .
Algumas vezes nos referiremos a CA1 e CB1 como semi-eixo maior e semi-eixo-menor
respectivamente, isto é, a e b respectivamente.
2
Problema 3 Uma elipse de excentricidade 𝑒 = 1/2 tem centro na origem, focos no eixo 𝑥 e
eixo maior igual a 12. Determine sua equação.
Problema 4 Uma elipse tem centro na origem e focos no eixo 𝑥. Determinar sua equação
sabendo que ela passa pelos pontos (0, −2) e (3, 0).
Ainda que não nos preocupemos com a demonstração o teorema abaixo nos será muito útil,
já que ele nos diz que se o eixo maior é horizontal ou vertical então a equação da elipse assume
uma forma simples.
Teorema 5 1) Um elipse possui eixo maior horizontal ( paralelo ao eixo 𝑥 ) se, e somente se,
sua equação pode ser escrita na forma
(𝑥 − 𝑥𝑐 )2 (𝑦 − 𝑦𝑐 )2
+
=1
𝑎2
𝑏2
onde 2𝑎 é o seu eixo maior, 2𝑏 seu eixo menor e (𝑥𝑐 , 𝑦𝑐 ) seu centro.
2) Um elipse possui eixo maior vertical ( paralelo ao eixo 𝑦 ) se, e somente se, sua equação
pode ser escrita na forma
(𝑦 − 𝑦𝑐 )2 (𝑥 − 𝑥𝑐 )2
+
=1
𝑎2
𝑏2
onde 2𝑎 é o seu eixo maior, 2𝑏 seu eixo menor e (𝑥𝑐 , 𝑦𝑐 ) seu centro.
As equações acima são conhecidas como equações reduzidas da elipse!!
Problema 6 Refaça os dois últimos problemas utilizando o teorema anterior.
Hipérbole
Definição 7 Sejam 𝐹1 e 𝐹2 dois pontos no plano. Seja ainda um número 2𝑎 positivo menor
que a distância entre 𝐹1 e 𝐹2 , distância esta que indicaremos por 2𝑐. Chamamos hipérbole de
focos 𝐹1 e 𝐹2 e eixo real 2𝑎 o conjunto de todos os pontos 𝑃 (𝑥, 𝑦) tais que
∣𝑃 𝐹1 − 𝑃 𝐹2 ∣ = 2𝑎,
ou ainda, módulo da diferença entre as distâncias de 𝑃 a 𝐹1 e distância de 𝑃 a 𝐹2 = 2𝑎.
Abaixo temos representada a hipeérbole de focos (1, 2) e (−1, −2) e eixo real 2𝑎 = 2.
𝐹 𝑖𝑔𝑢𝑟𝑎7.4
𝑦
...
.... ....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
.....
....
....
....
...
...
..
..
..
..
∙
..
..
..
..
..
...
...
.
..
..
..
..
...
.
..
..
..
..
...
..
..
..
..
..
.
..
..
..
..
..
...
..
..
..
..
..
.
..
..
..
..
..
...
.
..
..
..
..
...
.
..
..
..
..
..
..
...
.
..
..
..
...
..
..
..
∙
..
..
...
...
....
....
....
....
.....
.....
.....
.....
.....
.....
4
3
2
𝐹2
𝐹1
1
−4 −3 −2 −1
−1
−2
−3
−4
3
1
2
3
4
.....
..
𝑥
....
5
Problema 8 Determinar a equação da hipérbole acima.
𝑃 (𝑥, 𝑦) será um ponto da hipérbole se, e somente se, ∣𝑃 𝐹 1 − 𝑃 𝐹 2∣ = 2. Observe que,
emfunção do módulo é indiferente usarmos ∣𝑃 𝐹 1 − 𝑃 𝐹 2∣ = 2 ou ∣𝑃 𝐹 2 − 𝑃 𝐹 1∣ = 2. Logo,
teremos:
√
√
√
√
∣ (𝑥 − 1)2 + (𝑦 − 2)2 − (𝑥 − 4)2 − (𝑦 − 3)2 ∣ = 2 ⇔ (𝑥 − 1)2 + (𝑦 − 2)2 − (𝑥 − 4)2 + (𝑦 − 3)2 =
±2 ⇔
√
√
⇔ ( (𝑥 − 1)2 + (𝑦 − 2)2 )2 = ( (𝑥 − 4)2 + (𝑦 − 3)2 ± 2)2 ⇔
√
⇔ (𝑥 − 1)2 + (𝑦 − 2)2 = (𝑥 − 4)2 + (𝑦 − 3)2 ± 4 (𝑥 − 4)2 + (𝑦 − 3)2 + 4 ⇔
√
√
⇔ ±2 (𝑥 − 4)2 + (𝑦 − 3)2 = 3𝑥+𝑦 −12 ⇔ (±2 (𝑥 − 4)2 + (𝑦 − 3)2 )2 = (3𝑥+𝑦 −12)2 ⇔
⇔ −5𝑥2 + 3𝑦 2 − 6𝑥𝑦 + 40𝑥 − 44 = 0.
Tal como na elipse, identificamos certos elementos na hipérbole. Usamos a hipérbole acima
para identificar tais elementos. Observe.
𝐹 𝑖𝑔𝑢𝑟𝑎7.5
𝑦
..
..........
.....
..
.....
..
.....
..
.....
..
.....
..
.....
.
.....
.
.....
..
.....
..
.....
..
.....
...
..
.....
..
.....
.. ........∙
....
. .... .
....
............
....
.......... ....
.
...
.
.
.
.
.
.
.
.
...
...
...
...∙
.
.
.
.
.
.
.
.
....
.
.. .............
....
.
....
...........
....
∙....... .....
.....
..
.....
..
.....
.....
...
.....
...
.....
...
...
...
...
.
..
..
.....
..
.
..
...
.....
..
..
.
.
...
.
..
..
..
..
...
.
..
..
..
..
...
..
..
..
..
..
.
..
..
..
..
..
...
..
..
..
..
..
.
..
4
3
2
𝐴1
𝐹1
𝐴2 𝐹 2
1
−4 −3 −2 −1
−1
1
2
3
4
𝑥
5
−2
−3
−4
Focos: F1 e F2
Distância Focal: Distância 2𝑐 entre os focos
Vértices: Pontos A1 e A2
Centro: Ponto médio do segmento F1F2
Eixo real ou transverso: Segmento A1A2
Eixo imaginário ou conjugado: Segmento perpendicular ao eixo tranverso passando pelo
centro medindo 2𝑏 onde 𝑐2 = 𝑎2 + 𝑏2 .
Excentricidade: 𝑒 =
𝑐
𝑎
Uma hipérbole será dita equilátera se os eixos real e imaginário são iguais.
Novamente temos o teorema:
Teorema 9 1) Um hipérbole possui eixo real horizontal ( paralelo ao eixo 𝑥 ) se, e somente
se, sua equação pode ser escrita na forma
(𝑥 − 𝑥𝑐 )2 (𝑦 − 𝑦𝑐 )2
−
=1
𝑎2
𝑏2
4
onde 2𝑎 é o seu eixo real, 2𝑏 seu eixo imaginário e (𝑥𝑐 , 𝑦𝑐 ) seu centro.
2) Um hipérbole possui eixo real vertical ( paralelo ao eixo 𝑦 ) se, e somente se, sua equação
pode ser escrita na forma
(𝑦 − 𝑦𝑐 )2 (𝑥 − 𝑥𝑐 )2
+
=1
𝑎2
𝑏2
onde 2𝑎 é o seu eixo real, 2𝑏 seu eixo imagnário e (𝑥𝑐 , 𝑦𝑐 ) seu centro.
As equações acima são conhecidas como equações reduzidas da hipérbole!!
Problema 10 (a) Determine a equação reduzida da hipérbole 3𝑥2 − 𝑦 2 − 6𝑥 − 4𝑦 + 2 = 0
(b) Determine os eixos real e imaginário
(c) Faça o esboço da hipébole.
5