Lógica
Proposicional
Relações semânticas
entre conectivos e
formas normais
Conjunto de conectivos
completo


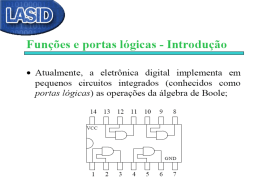
Um conjunto de conectivos é qualquer
conjunto cujos elementos sejam
conectivos (^, v, , , )
Num conjunto completo C, dada uma
fórmula H do tipo (P), (PvQ), (P^Q),
(PQ) ou (PQ), então é possível
determinar uma fórmula G, equivalente,
usando apenas os conectivos de C e os
símbolos proposicionais de H.
Exemplo de conjunto de
conectivos completo




{,v}
As fórmulas com conectivos {^,,} são
trocadas por equivalências com {,v}
Achar tautologias do tipo
(P*Q)  F, sendo



* € {^,,}
F expressa com {,v}
Equivalência entre ^ e {,v}


(P^Q)  (Pv  Q) é uma tautologia
(P^Q) e (Pv  Q) são equivalentes
Equivalência entre  e {,v}



(PQ)  (PvQ) é uma tautologia
(PQ) e (PvQ) são equivalentes
Resultado importante

Olha  sob o ponto de vista de
interpretação (valoração)
Equivalência entre  e {,v}


(P  Q)  ((P  Q)^(Q  P))
Substituindo  por seu equivalente


Substituindo ^ por seu equivalente


(P  Q)  ((P v Q)^(Q v P))
(P  Q)  ((P v Q)v(Q v P))
Está provada a completude de {,v}
Regra de substituição de
subfórmulas

Dadas as fórmulas da lógica proposicional
Eg, Eh, G e H onde




G é subfórmula de Eg
H é subfórmula de Eh e
Eh é obtida de Eg substituindo as ocorrências
de G em Eg por H
então se G equivale a H, Eg equivale a Eh
Transformação para o
conjunto {,v}

Dada uma fórmula E, como obter G
contendo apenas {,v}


Substituir PQ por
((P v Q)v(Q v P))


E=((P v Q)v(Q v P))v(R  S)
Substituir PQ por (Q v P)


e.g. E=(P  Q)v(R  S)
G=((P v Q)v(Q v P))v(RvS)
G equivale a E!
Conjunto {nand}



(P nand Q) = ((P^Q))
{nand} é completo!
Demonstração



Se {nand} puder expressar {,v}
P equivale a (P nand P) (1)
(PvQ) equivale a (P nand Q)

Lei de Morgan: (P ^ Q) equivale a (P v Q)
Transformação para o
conectivo nand



H=P^(RS)
Primeiro, transformar para {,v}
Depois transformar para nand, usando
as equivalências
P equivale a (P nand P)
 (PvQ) equivale a
((P nand P) nand (Q nand Q))
 (PvQ) equivale a
((P nand P) nand (Q nand Q))

Possível Redefinição da Linguagem
da Lógica Proposicional

Alfabeto


Símbolos de pontuação: (,)
Símbolos de verdade: false



true = false
Símbolos proposicionais: P, Q, R, S, P1, Q1, P2,
Q2...
Conectivos proposicionais: ,v
Formas normais e {,v,^}



Um literal é um símbolo proposicional
ou sua negação
Um bom conjunto completo é {,v,^}
Formas normais são obtidas a partir
desse conjunto de conectivos
Forma normal disjuntiva


Uma fórmula está na forma normal
disjuntiva (fnd ou DNF, em inglês) se é
uma disjunção de conjunções de literais
F é da forma F1 v F2 v ... v Fn, onde



Fi é uma conjunção (da forma
A1 ^ A2 ^ ... ^ An ) e
Ai é um literal
Ex: H=(P^Q) v (R^Q^P) v (P^S)
Forma normal conjuntiva


Uma fórmula está na forma normal
conjuntiva (fnc ou CNF, em inglês) se é
uma conjunção de disjunções de literais
F é da forma F1 ^ F2 ^ ... ^ Fn, onde



Fi é uma disjunção (da forma
A1 v A2 v ... v An ) e
Ai é um literal
Ex: G=(PvQ) ^ (RvQvP) ^ (PvS)
Obtenção de formas normais

Observe que H e G são parecidos



H=(P^Q) v (R^Q^P) v (P^S), DNF
G=(PvQ) ^ (RvQ vP) ^ (PvS), CNF
Para obtê-las a partir de fórmulas
quaisquer usam-se algoritmos duais

Tabela verdade: DNF usa o T e CNF usa o
F
Obtenção de formas normais a
partir de tabelas-verdade
H=(PQ) ^ R
 Pegam-se as linhas em que H=T
PQR H
T T T T L1
F T T T L2
F F T T L3
 L1=P^Q^R
 L2=P^Q^R
 L3=P^Q^R
 H=L1 v L2 v L3, DNF
 H=(P^Q^R) v (P^Q^R) v (P^Q^R)

PQR
TTT
TTF
TFT
TFF
FTT
FTF
FFT
FFF
H
T
F
F
F
T
F
T
F
Obtenção de formas normais
conjuntivas
H=(PQ) ^ R
 Pegam-se as linhas em que H=F
PQR H
TTF F
TFT F
TFF F
FTF F
FFF F
 H=L1 ^ L2 ^ L3 ^ L4 ^ L5, DNF
 H=(PvQvR) ^ (PvQvR) ^ (PvQvR)
^ (PvQvR) ^ (PvQvR)

PQR
TTT
TTF
TFT
TFF
FTT
FTF
FFT
FFF
H
T
F
F
F
T
F
T
F
Exercícios de obtenção de
formas normais


Obter DNF de (P ^Q) R
Obter CNF de (P ^Q) R
Algoritmos usando leis
(repetidamente)

1 -Leis de eliminação



2 -Lei da negação


(H)  H
2 -Leis de De Morgan



PQ = (PvQ)
P  Q = (P  Q)^(Q  P)
(PvQ) = P ^ Q
(P^Q) = P v Q
3 -Leis distributivas:


F v (G^H) = (FvG) ^ (FvH)
F ^ (GvH) = (F^G) v (F^H)
Exercícios

Obter DNF de (P v Q) R




= (PvQ) v R (eliminação de )
= (P ^ (Q)) v R (De Morgan)
= (P ^ Q) v R (negação)
Obter CNF de (P^(QR))S