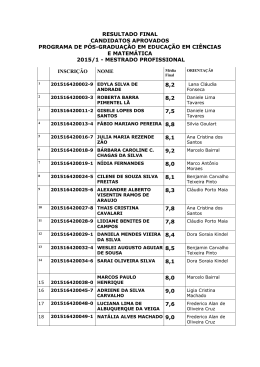
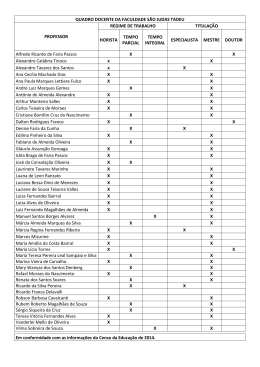
BAIRRAL, M.A.
1
APRENDER MATEMÁTICA NA CIBERCULTURA1
2
MARCELO ALMEIDA BAIRRAL
1. Pesquisa vinculada ao GEPETICEM/NEPPE. www.gepeticem.ufrrj.br;
2. Professor do Instituto de Educação, DTPE/ UFualJ, [email protected].
RESUMO: BAIRRAL, M.A. Aprender matemática na cibercultura. Revista Universidade Rural: Série
Ciências Humanas, Seropédica, RJ: EDUR, v. 27, n. 1-2, p. 91-97, jan.-dez., 2005. O desenvolvimento
e a construção da identidade do professor tem sido aspectos ressaltados da pesquisa educacional
contemporânea. E, os processos (meta) cognitivos na aprendizagem da matemática devem ser valorizados
pelas pesquisas interessadas na construção do conhecimento através da diversidade de práticas e do
trabalho colaborativo, por exemplo. Pode a tecnologia contribuir com a formação em matemática? Qual a
contribuição da Internet no ensino-aprendizagem de geometria? Nossas investigações tem como objetivo
analisar a importância da mediação tecnológica para o desenvolvimento profissional em geometria e apresentar
singularidades dos cenários virtuais à aprendizagem docente em matemática e aos princípios da eqüidade
na formação profissional do professor.
Palavras-chave: Desenvolvimento Profissional – Geometry – Educação a Distância - Internet.
ABSTRACT: BAIRRAL, M. A. Learning mathematics in the cyber culture. Revista Universidade
Rural: Série Ciências Humanas, Seropédica, RJ: EDUR, v. 27, n. 1-2, p. xx-xx, jan.-dez., 2005.
Professional development and the building of a teaching identity have been highlighted aspects of the
contemporary educational research. The cognitive and metacognitive processes in the mathematics learning
have to be encouraged by researches which are interested in building knowledge through a variety of
teaching practices and collaborative work. Is technology able to contribute with mathematics education?
What is the role of the internet in fostering geometry teaching and learning? Thus, we want to analyse the
importance of the technological mediation for a professional development in geometry, and show how
virtual communities are singularly able to help in it.
Key words: Professional development, geometry, distance learning and internet.
INTRODUÇÃO
Com as transformações sociais, o
grande avanço da tecnologia e a
repercussão desta nos meios educacionais,
novas formas de ensinar e de aprender
deverão ser reavaliadas, já que o professor,
elemento fundamental no processo ensinoaprendizagem, necessitará de um constante
aperfeiçoamento profissional e atualização,
garantindo assim a qualidade da ação
educativa. Nesta perspectiva, um grande
desafio da pesquisa sobre a prática
pedagógica é a relação teoria-prática e a
análise do trabalho de formação de um
professor reflexivo e crítico nas práticas de
auto-formação como aspectos do
desenvolvimento profissional (ANDRÉ,
1998).
No Brasil, embora a necessidade de um
trabalho de formação integradora para atuar
na Educação Básica em Matemática tenha
sido ressaltada pelas Diretrizes Curriculares
para a Formação de Professores (BRASIL,
1999), a importância de implementarmos
projetos de pesquisa que analisem o
desenvolvimento profissional nos processos
de formação e analisar a evolução do saber
docente dos professores em matemática,
ainda é incontestável (A Educação
Matemática em Revista, número especial
2002).
O professor é um profissional que deve
constantemente aprender a aprender
(PONTE, 1994). Umas das finalidades do
desenvolvimento profissional é tornar os
professores cada vez mais aptos a conduzir
um ensino de Matemática adaptado às
necessidades e interesses de cada aluno e
a contribuir para a melhoria das instituições
educativas (D‘AMBRÓSIO, 1999),
realizando-se, pessoal e profissionalmente.
Rev. Univ. Rural, Sér. Ci. Humanas. Seropédica, RJ, EDUR, v. 27, n. 1-2, jan.-dez., 2005. p. 91-97.
2
Para isso, a formação continuada, enquanto
dever do Estado (BRASIL, 1996, LDB, art.13,
inciso II), deve propiciar ao professor o uso
de ferramentas para enfrentar situações de
aprendizagem novas de tipos diferentes.
Uma dessas ferramentas é o desafio
tecnológico, que deve contribuir, entre outros
aspectos, para a transformação da escola
pública atual.
Conforme enfatizado no documento do
MEC, ¨a formação de professores à
distância justifica-se antes de mais nada
pelas dificuldades que muitos professores
enfrentam para participar de programas de
formação em decorrência da distância entre
os lugares em que vivem e os polos urbanos
onde se dão as ações de formação¨. No
entanto, no contexto educacional brasileiro,
as experiências de formação ‘a distância
ainda estão pautadas em dinâmicas de
trabalho presencial (Pátio Revista
Pedagógica, 2001) e, em matemática,
poucas (BORBA & PENTEADO, 2001)
estão promovendo a construção de cenários
que preconizem novas formas de aprender
também a distância ou na semipresencialidade.
Na Educação Matemática, diversas
pesquisas têm ressaltado a importância dos
conceitos geométricos tanto para contribuir
na formação integral dos alunos (BRASIL,
1997-1998), bem como para contribuir na
superação da insegurança ainda sentida
pelos professores no trabalho com os
mesmos (PIRES, 2001), uma vez que tais
conteúdos curriculares não foram objeto de
atenção no currículo de sua formação inicial.
Tradicionalmente, o ensino de geometria
tem se pautado em técnicas ultrapassadas.
Nos diferentes espaços de formação
profissional que atuamos, ainda temos
percebido a insegurança e medo de
professores e futuros professores quando
são colocados em situação de ensino em
geometria. No Brasil, as poucas pesquisas
em geometria focalizaram-se em três
Aprender matemática na cibercultura.
pontos: (a) o estabelecimento de níveis de
aprendizagem, (b) o uso do computador no
ensino e, (c) o desenvolvimento cognitivo dos
professores num processo de utilização das
novas tecnologias em situações
presenciais. Neste sentido, ampliar as
pesquisas e os projetos de atuação sobre
as influências do uso do computador como
instrumento de mediação (professorprofessor, professor-computador, professoratividade matemática) também na formação
continuada em geometria através da Internet,
irá trazer novas perspectivas para o processo
de desenvolvimento profissional docente e
na constituição de comunidades de
aprendizagem que contribuam com os
princípios de eqüidade (SECADA et al.,
1997) na Educação Publica Brasileira.
Assim, na perspectiva da formação
continuada de professores, considerando a
falta de atuações integradoras de pesquisa
e extensão no Brasil, nossos projetos
objetivam implementar e acompanhar
experiências formativas com atenção: (1) ao
desenvolvimento do conteúdo do
conhecimento profissional em matemática,
(2) à formação inicial e continuada à
distância/semi-presencial, (3) à criação de
ambientes virtuais de aprendizagem para a
geometria do Ensino Fundamental e, (4) as
interações profissionais que são
resignificadas com a mediação através das
ferramentas da Internet.
MATERIAL E MÉTODOS
Nossas investigações fazem parte de um
grande projeto para formação inicial e
continuada docente em matemática, que
está sendo desenvolvido desde agosto de
2000 no campus virtual da UFRuralRJ. A
seguir apresentaremos elementos
metodológicos estratégicos dos cenários
virtuais que constituem objeto de estudo de
cada pesquisa.
Rev. Univ. Rural, Sér. Ci. Humanas. Seropédica, RJ, EDUR, v. 27, n. 1-2, jan.-dez., 2005. p. 91-97.
BAIRRAL, M.A.
Estruturação do Conteúdo e Integração
Curricular
Apesar de centrarmos atenção à
geometria, as atividades propostas ao longo
da pesquisa têm uma perspectiva
integradora com outras áreas da
matemática. Além do mais, buscando
despertar os participantes para a
necessidade de inserir em suas aulas
temas que perpassam as diferentes áreas
curriculares e que são fortemente
importantes na formação de um cidadão
comprometido com mudanças sociais
significativas, a transversalidade é um
elemento curricular integrador preconizado
pelas tarefas formativas e que está em
constante discussão em todo o
desenvolvimento das teleinterações no
ambiente de aprendizagem. Nesta
perspectiva, geometria, arte, linguagem e
ciência fazem parte de nossa proposta para
o desenvolvimento de um conhecimento
profissional integrador.
Considerando o (futuro) professor como
autor do seu próprio conhecimento e que
este está em constante desenvolvimento e
processo de apropriação de significados,
nossos ambientes virtuais são estruturados
em 6 eixos hipertextuais: (a) atividade que
objetiva uma revisão dos próprios
conhecimentos geométricos e das distintas
ações profissionais dos professores, (b)
observação do papel que assume o cotidiano
nas distintas atividades geométricas, (c)
reconstrução de processos cognitivos dos
alunos em classe, (d) reconhecimento e
atenção para o uso de recursos em cada
tema estudado, (e) síntese organizada do
conteúdo e, (f) atenção à importância da
avaliação continuada. Após a seleção das
tarefas, os participantes podem traçar o
caminho hipertextual que desejarem.
Assim, pensamos que além de propormos
ferramentas de valor cognitivo que ajudem
o professor na realização e comunicação
das tarefas, estamos dando autonomia de
trabalho ao professor.
3
Material e Acessibilidade ao Ambiente
Virtual Formativo
Reconhecendo a importância da
motivação, da auto-aprendizagem e da
teleinteratividade, nossos ambientes
possuem variados componentes
motivacionais, tais como: fotos de professor
em sala com seus alunos, fotos de alunos
em ação, quadro diálogo (que se abre
quando é acessada a página e aparece uma
fala, constantemente mudada, de um dos
professores), imagens com movimentos,
vínculos para eventos diversos e outras
novidades educacionais. Os pontos de
interatividade são outras ferramentas que
também propiciarão o caminhar hipertextual
pelo ambiente (e fora dele) e a teleinteração
contínua entre todos os participantes do
curso. Cada um deles possui uma função
importante no desenvolvimento hipertextual
da dinâmica de trabalho virtual, tais como:
livros e demais trabalhos disponíveis na
rede; enlace à página do MEC, na qual o
professor pode acessar os Parâmetros
Curriculares Nacionais e outros
documentos oficiais; artigos e links a
leituras inerentes a temática de cada
unidade.
O acesso a cada ambiente, que poderá
ser feito de qualquer computador conectado
à Internet, se dá através de uma senha
pessoal, recebida pelo docente no ato de
sua inscrição. Visando reduzir ao máximo
para o professor o custo com o curso, todo
o material está disponível em rede e ele
pode, como e quando lhe convier, imprimílo, salvá-lo em disquete, etc. Todas as
tarefas de formação são disponibilizadas em
arquivos do word e o participante poderá
realizá-las sem estar conectato e, caso
esteja, poderá acessar aos diferentes links
opcionais que são sugeridos para o
desenvolver das mesmas. No entanto ter a
possibilidade de imprimir as atividades, lêlas e discutí-las, inclusive com os seus
colegas de trabalho, outros atores
importantes
na
construção
do
conhecimento, é um componente
motivacional importante ao desenvolvimento
profissional do professor.
Rev. Univ. Rural, Sér. Ci. Humanas. Seropédica, RJ, EDUR, v. 27, n. 1-2, jan.-dez., 2005. p. 91-97.
4
Formas de Interação
No desenvolvimento das pesquisas as
teleinterações são distintas e de diferentes
níveis. Enquanto o e-mail permite um contato
mais personificado, a lista de discussão é
uma ferramenta comunicativa à qual todos
poderão acessar, ver o que está sendo
discutido e participar da discussão, com um
tempo próprio para reflexão e resposta.
Todas as atividades desenvolvidas pelos
cursistas são enviadas por e-mail ao
formador e algumas também são enviadas
para a lista de discussão, para que se
possam enriquecer e aprofundar aspectos
de cada unidade didática considerados
relevantes pelo coletivo profissional.
Além de algumas tarefas que
necessitam realizar coletivamente, os
integrantes do cenário virtual podem
comunicar-se continuamente também entre
si e com o formador em tempo real ou
diferido e, também, com o técnico que
acompanha todo o curso para assessorar
em problemas de informática. Assim,
distintas são as teleinterações que são
estabelecidas entre os professores
(realização conjunta de tarefas, intervenções
no fórum de discussão ou participação nos
chats), entre cada professor e o formador
(troca de mensagens eletrônicas, envio de
arquivos e tarefas, auto-avaliação ao final
de cada unidade didática, etc.). Enfim,
todas as formas de interação são
incentivadas e valorizadas. Também são
previstas interações por telefone com a
equipe coordenadora, cujo número e horário
de atendimento são divulgados na ocasião
do início do curso.
Coleta de Dados e Avaliação
A coleta de dados é realizada a partir de
diversas fontes de informação, ou seja,
interações docentes em tempo real ou
diferido. Em tempo real utilizamos chats
(opcionais e obrigatórios), entrevista,
filmagem e mensagem do ICQ ou MSN. Em
tempo diferido temos: e-mails (autoavaliação, ficha de inscrição, contrato de
trabalho, planejamentos e relatos de aula,
Aprender matemática na cibercultura.
realização e envio de tarefas), fórum de
discussão e questionários semiestruturados. A informação proveniente
dessas distintas teleinterações, juntamente
com as observações e análise do
investigador em seu diário de campo,
constituem a triangulação dos dados na
pesquisa.
Além das especificidades dos conceitos
geométricos trabalhados, dos diferentes
tipos de mensagens eletrônicas trocadas,
cada integrante também será avaliado
considerando sua participação na lista de
discussão e nos chats obrigatórios, o envio
das tarefas no prazo estabelecido e demais
contribuições e produções ao longo do
curso. Assim, a avaliação tem caráter
processual para o qual a policemia de
instrumentos anteriormente apresentada,
constitui uma rica prática comunicativoavaliativa (BAIRRAL, 2001, 2002, 2003b).
PESQUISAS EM DESENVOLVIMENTO
O GEPETICEM (Grupo de Estudos e
Pesquidas das Tecnologias da Informação
e Comunicação em Educação Matemática:
www.gepeticem.ufrrj.br), fundado em outubro
de 1999, está vinculado ao NEPPE (Núcleo
de Estudos e Pesquisas em Política
Educacional, cadastrado no CNPq) do
Instituto de Educação da UFRuralRJ/DTPE.
O GEPETICEM tem desenvolvido pesquisas
em colaboração com a Universidade de
Barcelona (Espanha). Obteve financiamento
da CAPES e, atualmente, conta com apoio
do CNPq (PIBIC-UFRuralRJ) e da SESu/
MEC (Dext/UFRuralRJ). A seguir
apresentamos os objetivos das pesquisas
que estamos desenvolvendo: (1) identificar
e analisar significados produzidos por alunos
do ensino médio para elementos da
geometria espacial (mestrado); (2) analisar
elementos do discurso do tutor-formador no
processo teleinterativo (mestrado); (3)
inventariar ambientes que estão sendo
implementados no Brasil via Internet (PIBIC/
CNPq-UFRuralRJ); (4) elaborar, implementar
Rev. Univ. Rural, Sér. Ci. Humanas. Seropédica, RJ, EDUR, v. 27, n. 1-2, jan.-dez., 2005. p. 91-97.
BAIRRAL, M.A.
5
e avaliar um cenário virtual geométrico como
disciplina da graduação em matemática da
UFRuralRJ (PIBIC); (5) analisar processos
cognitivos de estudantes na construção dos
diferentes espaços geométricos; (6) analisar
impactos da graduação em matemática à
distância do CEDERJ na região de
Paracambi; (7) verificar a influência de uma
sequência de atividades com APPLETS na
aprendizagem de geometria; e (8) estudar
implicações da multimodalidade num
ambiente virtual para a formação continuada
em geometria (MEC/SESu).
DISCUSSÃO
A base principal das práticas de
qualidade nos projetos e processos de
educação é garantir continuamente
melhorias na criação, aperfeiçoamento,
divulgação de conhecimentos culturais,
científicos, tecnológicos e profissionais que
contribuam para superar os problemas
regionais, nacionais e internacionais e para
o desenvolvimento sustentável dos seres
humanos, sem exclusões, nas
comunidades e ambientes em que vivem
(MEC/SEED, 2000). Assim, para o
estabelecimento de programas eficientes de
educação a distância em geral e,
especialmente em matemática, STEPHEN
et al. (1996) ressaltaram a necessidade de
considerarmos
como
princípios
fundamentais: o da cooperação (diferentes
e valiosas formas de colaboração, em todos
os
estágios
do
planejamento,
desenvolvimento, implementação e
avaliação dos programas), o princípio da
cultura e linguagem (necessidade de
considerar as variações lingüísticas e
culturais), e o princípio da eqüidade (garantir
formação que responda às expectativas e
necessidades dos diferentes indivíduos ou
grupos sociais).
No processo interativo são relevantes as
contribuições de cada espaço comunicativo
e suas especificidades (BAIRRAL, 2001).
Não se trata de valorizar um instrumento
em detrimento do outro, pois é na utilização
diferenciada dos mesmos que o processo
comunicativo
se
enriquece
e,
conseqüentemente, o formador tem mais
elementos sobre o desenvolvimento
profissional dos participantes. Além da
integração de cada espaço na atividade
virtual
formativa
(tarefa+interação+colaboração),
é
importante que haja um equilíbrio entre a
quantidade de espaços de interação em
tempo real com os mediadores em tempo
diferido (BAIRRAL, 2003a).
Visando a construção de uma sociedade
mais justa e tecnodemocrata (LÉVY, 1998)
e a ruptura dos espaços e tempos na busca
de intercâmbio de informação e, desta
forma, construir novas metáforas de espaço
social para facilitar os processos interativos,
autônomos e críticos, seguimos investindo
na formação a distância como uma das
estratégias de formação profissional,
principalmente num país de grande extensão
territorial e com dificuldade de acesso ao
conhecimento oficial, como é o caso do
Brasil. No entanto, considerando as
especificidades educacionais brasileiras,
gostaríamos de concluir ressaltando
algumas dificuldades ainda vigentes e que
devemos superá-las no campo da formação
via Internet (BAIRRAL et al., 2001).
A primeira se refere à necessidade de
aumentarmos as formas de comunicação
entre os professores participantes que
contemplem mais interação em vídeo
conferências, por exemplo. Como segundo
desafio, não basta apenas aumentarmos a
comunicação docente se não propiciarmos
ao professor oportunidades concretas de
discutir sua prática (meta)cognitivamente,
a partir de análise de situações concretas
do que faz o docente em sala de aula
(análise de vídeos, incidentes críticos, etc.).
Neste sentido a tipologia das tarefas de
formação assumem papel primordial.
O terceiro desafio é dotar a instituição
proponente de uma infra-estrutura (telefone,
fax, equipamentos de informática em geral),
não apenas para elaboração e
Rev. Univ. Rural, Sér. Ci. Humanas. Seropédica, RJ, EDUR, v. 27, n. 1-2, jan.-dez., 2005. p. 91-97.
6
implementação de cursos, mas para
subsidiar o acompanhamento ao longo de
todo o processo formativo, visando auxiliar
o participante em todas as suas
dificuldades, incluindo as técnicas. A
composição de uma equipe multidisciplinar
é outro desafio a ser vencido, ou seja, além
dos professores especialistas, devemos ter
profissionais das demais áreas do
conhecimento, inclusive a participação de
profissionais das tecnologias da informação
e comunicação (STEPHEN et al., 1996;
MEC/SEED, 2000). Estes dois desafios já
estão sendo minimizados através da
inserção de suporte informático em
colaboração com a COINFO/UFRuralRJ e
dos graduandos em matemática da
UFRuralRJ.
O real envolvimento e a co-participação
das secretarias (estaduais, municipais) de
educação e demais organizações
governamentais ou não, se fazem
importantes no tocante a atenção especial
para realidades curriculares locais e, como
enfatizaram STEPHEN et al. (1996), para o
mais importante, que é tornar o processo
de formação a distância também como
objeto de pesquisa.
Como um último desafio, é
imprescindível que o (futuro) professor tenha
reais condições econômicas (i) para uma
infra-estrutura informática, seja em sua
própria residência ou em sua escola, de
maneira que possa acessar e ter disponível,
incluso impresso, todo o material
necessário para o acompanhamento no
curso, e (ii) para que disponha de tempo
suficiente para investir seriamente em seu
desenvolvimento profissional. Finalizando,
cursos a distância, por Internet ou não,
devem pautar-se para colaborar com uma
formação de qualidade, não massificadora
e de reais possibilidades de acesso e
continuidade de formação para todos os
nossos profissionais (BAIRRAL, 2001).
Aprender matemática na cibercultura.
REFERÊNCIAS BIBLIOGRÁFICAS
A Educação Matemática em Revista.
Publicação Semestral da Sociedade
Brasileira de Educação Matemática
(SBEM). São Paulo, n. 11A, abril/2002.
ANDRÉ, M. Desafios da Pesquisa Sobre a
Prática Pedagógica. In Anais II (1/1) do IX
ENDIPE. Águas de Lindóia/SP, 1998, p.
257-266.
BAIRRAL, M. Dimensões de Interação na
Formação à Distância em Matemática.
Erechim-RS, Revista Perspectiva, v. 27, n.
98, p. 33-42, jul./2003a.
BAIRRAL, M. Debate Virtual y Desarrollo
Profesional. Una Metodología para el
Análisis del Discurso Docente. Madrid,
Revista de Educación, 2003b. No prelo.
BAIRRAL, M.A. Aprender a Aprender
Matemática no ¨CiberEspaçoFormação¨.
Pátio Revista Pedagógica, Porto Alegre, n.
26, ano VII, mai./jul. 2003c, p. 32-35.
BAIRRAL, M.A. Desarrollo Profesional
Docente en Geometría: Análisis de un
Processo de Formación a Distancia.
Universidade de Barcelona. Tese de
Doutorado publicada eletronicamente em 08/
10/2002 (http://www.tdcat.cesca.es/TDCat1008102-120710.
BAIRRAL, M.A. Comunicação Docente:
Perspectivas para o Desenvolvimento
Profissional pela Internet. Pátio Revista
Pedagógica. Porto Alegre, n. 18, p. 37-39,
ago./out. 2001.
BAIRRAL, M.A.; GIMÉNEZ, J. & TOGASHI,
E. Desenvolvimento profissional docente
baseado na WEB: perspectivas para a
Educação Geométrica. Rio de Janeiro,
Boletim GEPEM nº 39, p. 25-36, set./2001.
Rev. Univ. Rural, Sér. Ci. Humanas. Seropédica, RJ, EDUR, v. 27, n. 1-2, jan.-dez., 2005. p. 91-97.
BAIRRAL, M.A.
BRASIL: Ministério da Educação –
Indicadores de qualidade para cursos de
graduação a distância. SEED-Secretaria de
Educação a Distância, 2000.
BRASIL: Ministério da Educação
Referencial para Formação de Professores.
Brasilia, Secretaria de Educação
Fundamental, 1999.
BRASIL: Ministério da Educação
Parâmetros Curriculares Nacionais. Brasilia,
Secretaria de Educação Fundamental,
1997-1998.
BRASIL, Congresso Nacional. Lei de
Diretrizes e Bases da Educação Brasileira.
Nº 9394/1996. In: Diário Oficial da União,
Ano CXXXIV, nº 248, 23. 12.12.1996,
(p.27.833-27.841).
BORBA, M. & PENTEADO, M. Informática
e Educação Matemática. Belo Horizonte:
Autêntica, 2001.
D‘AMBRÓSIO, U. Entrevista concedida para
A Educação Matemática em Revista, n. 7,
p. 5-10, 1999.
7
LÉVY, P. As tecnologias da inteligência. Rio
de Janeiro: Editora 34, 1998, 6. ed.
Pátio Revista Pedagógica. Educação a
Distância. Porto Alegre: ARTMED, n. 18,
ago./out. 2001.
PIRES, C.M.C. et al. Espaço e forma: a
construção de noções geométricas pelas
crianças das quatro séries iniciais do Ensino
Fundamental. São Paulo: PROEM, 2001.
PONTE, J.P. da. Mathematics Teachers
Professional Knowledge. In Proceedings of
the Eighteenth International Conference
PME. Lisboa, v. 1, p. 195-210, 1994.
SECADA,
ADAJIAN,
enseñanza
tendencias.
W.G.; FENNEMA, E. &
L.B. (comps.) Equidad y
de las matemáticas: nuevas
Madrid: MEC/MORATA, 1997.
STEPHEN, A.; SHIU, C. & ELLERTON, N.
Critical Issues in the Distance Teaching of
Mathematics and Mathematics Education.
In: BISHOP et al. (eds.) International
Handbook of Mathematics Education, 701753, 1996.
Rev. Univ. Rural, Sér. Ci. Humanas. Seropédica, RJ, EDUR, v. 27, n. 1-2, jan.-dez., 2005. p. 91-97.