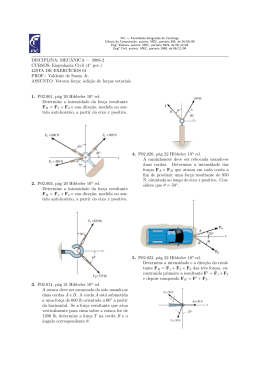
Capı́tulo 4
O Tensor das tensões
As forças que as moléculas exercem umas sobre as outras são geralmente forças de
alcance muito curto em comparação com as dimensões dos corpos de que essas moléculas
fazem parte e que se apresentam à nossa experiência macroscópica. Assim, essas forças
podem mesmo considerar-se de alcance nulo. Isto é, as forças que as partı́culas dos
corpos macroscópicos exercem entre si apresentam-se como forças de contacto. Os
corpos existentes exercem acções mútuas somente através das partes que se tocam.
4.1
O vector tensão
Consideremos uma superfı́cie infinitésimal no seio dum meio contı́nuo (ou separando
dois meios distintos). Seja dS a área dessa superfı́cie. A resultante df das forças que
as partı́culas situadas dum dos lados da referida superfı́cie exercem sobre as partı́culas
situadas do outro lado é, evidentemente, proporcional a dS (se dS duplicar, duplica
df , se dS triplicar, triplica df ). Temos pois
df = tdS.
(4.1)
A tensão t é constante em cada ponto, independente de dS, desde que a orientação
da superfı́cie não varie. Para outra superfı́cie elementar, na vizinhança da anterior,
mas com orientação diferente, já o coeficiente entre a força que se exerce através da
superfı́cie e a área da superfı́cie toma um valor diferente. Isto é, a tensão t é função
da orientação da superfı́cie a que se refere. Essa orientação é definida pela normal n̂ à
superfı́cie. É costume considerar a tensão t que as partı́culas que estão do lado para o
qual aponta a normal n̂ exercem sobre as partı́culas que estão do outro lado e designar
essa tensão por t(n̂),
df = t(n̂)dS
(4.2)
Pergunta-se: como é que t(n̂) varia com n̂? Para encontrarmos a resposta a esta pergunta consideremos um tetraedro elementar, constituı́do por uma superfı́cie arbitrária
que intersepte um triedo de referência com origem no ponto que se deseje considerar
e definido por três eixos ortogonais, de versores ê1 , ê2 e ê3 . Seja dS a área da face
do tetraedro que intersepta os três eixos. Seja dSi a área da face normal ao versor
êi . O elemento de superfı́cie dS1 é, evidentemente, a projecção de dS sobre o plano
42
coordenado definido pelos versores ê2 , ê3 , e analogamente para dS2 e dS3 . Designando
por n̂ a normal exterior a dS, o ângulo de dS com dS1 é evidentemente igual ao ângulo
das respectivas normais, n̂ e ê1 .
x3
^n
^ e ^
3
e
2
^
e
1
x2
x1
Figura 4.1: Tetraédro em equilı́brio
Isto é,
dSi = (n̂ · êi )dS
(4.3)
Estando o tetraedro elementar em equilı́brio, a resultante das forças que o meio exterior
exerce sobre o meio interior é evidentemente nulo. Pode haver forças de volume, mas
sendo proporcionais ao volume, são infinitesimais de ordem superior e devem desprezarse em comparação com as forças de superfı́cie, que são proporcionais à superfı́cie (o
coeficiente entre o volume e a superfı́cie dum poliedro tende para zero com as dimensões
do poliedro).
Sobre o tetraedro exercem-se as seguintes forças: t(n̂)dS sobre dS, e t(−êi )dSi sobre
dSi . Escrevemos t(−êi ) e não t(êi ) porque se trata da tensão que a parte de fora exerce
sobre a parte de dentro e é −êi o versor que aponta para fora. Visto que a resultante
das forças é nula, podemos escrever
t(n̂)dS +
3
X
t(−êi )dSi = 0
(4.4)
t(−êi )(n̂ · êi )dS = 0
(4.5)
i=1
e, visto que dSi = n̂ · êi dS, vem
t(n̂)dS +
X
i
43
dividindo por dS,
t(n̂) = −
X
t(−êi )(n̂ · êi ).
(4.6)
i
Daqui se segue que t(n̂) = −t(−n̂), o que está de acordo com o princı́pio da igualdade
da acção e da reacção e que nos permite escrever
X
t(n̂) =
t(êi )(n̂ · êi ).
(4.7)
i
Esta equação resolve a questão posta: para conhecermos t(n̂) para um n̂ arbitrário
basta-nos conhecer 3 valores particulares de t(n̂), as quantidades t(ê1 ), t(ê2 ) e t(ê3 ).
Este resultado é muito importante. Seja n̂ · êi = ni então
t(n̂) =
3
X
t(êi )ni .
i=1
Este resultado é uma consequência do teorema da quantidade de movimento: se o
tetraedro elementar está em equilı́brio a resultante das forças que actuam sobre ele é
nula.
4.2
Construção do tensor das tensões
Decompondo o vector t(êi ),
3
X
σij êj
(4.8)
3
X
tj (n̂)êj
(4.9)
3
X
σij ni
t(êi ) =
j=1
e o vector t(n̂)
t(n̂) =
j=1
temos de (4.7)
tj =
(4.10)
j=1
Note-se o significado de σij : é a componente segundo êj de t(êi ). As quantidades σij
são em número de nove e constituem um tensor.
Problema:
Provar que as quantidades σij constituem um tensor.
44
Resolução:
a) Método indicial
No sistema S temos
tj =
X
σij ni .
(4.11)
X
0
σkm
n0k .
(4.12)
i
No sistema S temos
0
t0m =
k
Note-se que as quantidades tj ou são componentes dum vector e as quantidades
ni ou n0k são componentes dum vector de orientação arbitrária (t é a tensão através
duma superfı́cie de orientação arbitrária definida pela normal n̂)
t0m
Então temos
t0m =
X
αmj tj
n0k =
j
X
αki ni ,
(4.13)
i
ou seja,
X
0
σkm
n0k =
onde usámos tj =
i
αmj tj =
j
k
P
X
XX
j
αmj σij ni ,
i
σij ni , ou ainda
XX
XX
0
σkm
αki ni =
αmj σij ni
i
k
j
(4.14)
(4.15)
i
Esta igualdade tem de verificar-se qualquer que seja a orientação de n̂. Fazendo
n1 = 1, n2 = 0, n3 = 0, vem
X
X
0
σkm
αk1 =
αmj σ1j .
(4.16)
j
k
Fazendo n1 = 0, n2 = 1, n3 = 0, vem
X
X
0
σkm
αk2 =
αmj σ2j .
(4.17)
Fazendo n1 = 0, n2 = 0, n3 = 1, vem
X
X
0
σkm
αk3 =
αmj σ3j .
(4.18)
j
k
j
k
Portanto ,
X
0
σkm
αki =
X
αmj σij
(4.19)
j
k
qualquer que seja i. Multiplicando ambos os membros por αgi e somando em
ordem a i vem
XX
XX
0
σkm
αki αgi =
αmj σij αgi .
(4.20)
i
i
k
45
j
Usando a condição de ortogonalidade
X
αki αgi = δkg
(4.21)
i
temos finalmente
X
0
0
σkm
δkg = σgm
=
XX
i
k
αgi αmj σij .
(4.22)
j
Portanto, as quantidades σij são componentes dum tensor.
b) Método matricial
Sejam t, n, T as matrizes (matrizes colunas ou matrizes quadradas, conforme os
casos) que representam os vectores t e n e o tensor σij no sistema S. Sejam t0 , n0 , T 0
as matrizes que representam as mesmas quantidades no sistema S 0 . Então
t̃ = ñ T,
t̃0 = ñ0 T 0
(4.23)
t0 = αt,
n0 = αn,
(4.24)
t̃0 = t̃α̃,
ñ0 = ñα̃.
(4.25)
Ora
logo,
Portanto,
t̃0 = t̃α̃ = ñ0 T 0 = ñα̃ T 0 = ñ T α̃,
(4.26)
ñ T α̃ = ñα̃ T 0 .
(4.27)
isto é
Sendo n arbitrário podemos escrever
T α̃ = α̃ T 0 .
(4.28)
Multiplicando à esquerda por α e usando a condição de ortogonalidade αα̃ = I,
vem
T 0 = αT α̃.
(4.29)
que corresponde à lei de transformação de um tensor.
4.3
Expressão da força de tensão por unidade de
volume
Consideremos uma superfı́cie fechada, com a forma de um paralelepı́pedo rectângulo de
faces paralelas aos eixos x1 , x2 e x3 , situada num meio contı́nuo. Queremos determinar
a resultante das forças que o meio exterior exerce sobre o meio interior. Comecemos
por considerar as forças exercidas segundo a direccção do eixo dos x1 , primeiro nas
faces perpendiculares a x1
46
x2
σ11( x1
)
σ11 ( x 1 +dx 1 )
dx1
x1
x
x1
x 1 +dx 1
3
Figura 4.2: Cubo em equilı́brio
dF1 (1) = σ11 (x1 + dx1 ) dx2 dx3 − σ11 (x1 ) dx2 dx3 =
∂σ11
dx1 dx2 dx3
∂x1
Sobre as faces perpendiculares a x2 , temos
dF1 (2) = σ21 (x2 + dx2 ) dx1 dx3 − σ21 (x2 ) dx1 dx3 =
∂σ21
dx1 dx2 dx3 ,
∂x2
e sobre as faces perpendiculares a x3
∂σ31
dx1 dx2 dx3 .
∂x3
Somando a três contribuições, e dividindo por dV = dx1 dx2 dx3 obtemos para a força
por unidade de volume na direcção do eixo x1
dF1 (3) = σ31 (x3 + dx3 ) dx1 dx2 − σ31 (x3 ) dx1 dx2 =
3
∂σ11 ∂σ21 ∂σ31 X ∂σi1
dF1
=
+
+
=
.
f1 =
dV
∂x1
∂x2
∂x3
∂x
i
i=1
Procedendo de um modo semelhante para as outras componentes, obtemos
∂σ12 ∂σ22 ∂σ32
dF2
f2 =
=
+
+
dV
∂x1
∂x2
∂x3
dF3
∂σ13 ∂σ23 ∂σ33
f3 =
=
+
+
,
dV
∂x1
∂x2
∂x3
ou ainda
3
X
∂σij
.
fj =
∂xi
i=1
Vectorialmente poderia escrever-se
f=
3
X
∂t(êi )
i=1
47
∂xi
.
(4.30)
4.4
4.4.1
Condições de Equilı́brio
Condições de equilı́brio local
Consideremos um dado meio material em equilı́brio. Seja dV = dx1 dx2 dx3 um volume
elementar no seio desse meio. Sobre dV actuam além das forças de tensão, forças
volúmicas tais como a força da gravidade. Representemos as forças volúmicas que
actuam na unidade de massa por F e por ρ a densidade do meio material. A condição
de equilı́brio local, a resultante das forças que actuam sobre dV é nula, pode ser
expressa através da equação
∂σij
+ ρFj dV = 0
(4.31)
∂xi
ou, visto que dV é arbitrário,
∂σij
+ ρFj = 0.
∂xi
4.4.2
(4.32)
Condições de equilı́brio dos momentos das forças
Além do equilı́brio de forças, é também necessário impor que o momento resultante
das forças aplicadas seja nulo. Devemos tomar em conta a contribuição das tensões e
das forças volúmicas, como a força da gravidade. Consideremos primeiro o momento
das forças de tensão sobre um cubo de material de arestas dx1 , dx2 , dx3 e volume
dV = dx1 dx2 dx3 . Os binários que contribuem para para a componente do momento
das forças na direcção do eixo x3 , são os indicados na figura.
x2
σ
21
dx1
σ
12
σ
12
dx2
x1
σ
21
x3
Figura 4.3: Tensões que contribuem para M3
48
Temos, assim
M3 = (σ12 dx2 dx3 ) dx1 − (σ21 dx1 dx3 ) dx2 = (σ12 − σ21 ) dx1 dx2 dx3 .
De um modo semelhante obtemos para as outras componentes da resultante dos momento das forças de tensão aplicadas
M1 = (σ23 dx1 dx3 ) dx2 − (σ32 dx1 dx2 ) dx3 = (σ23 − σ32 ) dx1 dx2 dx3 .
M2 = (σ31 dx2 dx3 ) dx1 − (σ13 dx1 dx2 ) dx3 = (σ31 − σ13 ) dx1 dx2 dx3 .
~ v | ∼ ρF dx1 dx2 dx3 d`
O momento correspondente à força de volume é da ordem |M
onde d` é o braço da força e é da ordem de grandeza de dxi . Os comprimentos dxi são
infinitesimais e, por isso, o momento das forças volúmicas é uma ordem de grandeza
inferior ao momento das forças de tensão e por isso podemos desprezá-lo em relação a
esta últimas. Concluı́mos que
~ = 0 → M1 = 0,
M
ou ainda σ12 = σ21 ,
4.4.3
, M2 = 0,
M3 = 0.
σ13 = σ31 , σ32 = σ23 . O tensor das tensões é simétrico.
Condições de Fronteira
As forças de tensão num dado material são de um modo geral resultantes da aplicação
de forças exteriores sobre a sua superfı́cie. Representamos por P a força exterior por
unidade de área sobre a superfı́cie. Por outro lado sobre a superfı́cie actuam também
as forças de tensão t(−n̂) onde n̂ é a normal à superfı́cie exterior. A fronteira está em
equilı́brio se a resultante das forças que actuam sobre ela se anularem i.e. se
PdS + t(−n̂)dS = 0
(4.33)
P = t(n̂).
(4.34)
ou
Projectando segundo os diferentes eixos obtemos
Pi =
3
X
σji nj .
(4.35)
j=1
Se sobre a fronteira não actuarem forças exteriores a condição de equilı́brio reduz-se a
3
X
σji nj = 0.
(4.36)
j=1
Se impusermos as condições de equilı́brio a uma superfı́cie de separação de dois meios
materiais temos
3
3
X
X
(2)
(1)
(4.37)
nj σji ,
nj σji =
j=1
j=1
(1)
σji ,
(2)
σji
representam as componentes do tensor das tensões sobre a superfı́cie,
onde
respectivamente, nos meios 1 e 2.
49