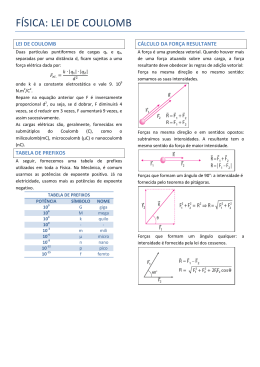
Calcule a intensidade da resultante das forças elétricas q atuam na partícula “C”(a
partícula C localiza-se no encontro das diagonais do quadrado).Obs: A figura é um
quadrado de lado: √2 cm(raiz quadrada de 2 cm)
A
B
E
D
Dados: Qa=Qb= 2mC
Qc= - 2mC
Qd=Qe= -2mC
K= 9.10^9 Nm²/C²
Note que cargas de mesmo sinal se repelem e que cargas de sinal oposto se atraem,
assim as forças sobre a carga C são:
Fec é a força da carga E sobre a carga C –> é força de repulsão.
Fac é a força da carga A sobre a carga C –> é força de atração.
Fdc é a força da carga D sobre a carga C –> é força de repulsão
Fbc é a força da carga B sobre a carga C –> é força de atração.
Note que todas essas forças têm o mesmo módulo. Basta calcular uma delas portanto. E
∣Q1∣.∣Q2∣
para isso você vai usar a lei de Coulumb. F = k.Q1.Q2 / d² F =k.
d²
Sendo d a distância entre as cargas, que é igual, pelo que se pode ver na figura, metade
do diâmetro.
Bem, trata-se de um quadrado de lado
 2 logo a diagonal mede:



D =  2 ² 2 ²= 4=2 .
Como a distância d é a metade do diâmetro: d = 2 cm = 2.10-2 m
Assim você já pode determinar o valor das forças.
A força resultante é a soma vetorial Você pode calcular primeiro a soma vetorial de Fac
com Fbc lembrando que formam entre si 90°, basta usar o Teorema de Pitágoras ( o
mesmo teorema que usei para achar a diagonal do quadrado).
A soma de Fec com Fdc é igual, em módulo, direção e sentido à soma de Fac com Fbc,
de forma que você não vai precisar calcular de novo.
Assim você ter as duas forças que eu marquei na figura como F1 e F2 , iguais e com a
mesma orientação. A resultante final vai ser a soma simples Fr = F1 + F2 .
Cuide apenas com o valor da carga. Você escreveu a unidade assim “mC” que é o
símbolo de “mili coulomb” , 1 mili coulomb é igual a 1.10-3 coulombs.
Mas verifique em seu livro (ou onde for) se o correto não seria “μC” que é o “micro
coulomb”, veja que 1 micro coulomb é igual a 1.10-6 coulombs.
Qualquer dúvida torne a entrar em contato.
Att
Sandro