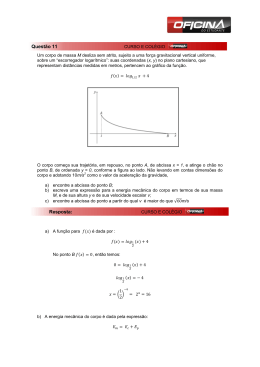
CONJUNTOS NUMÉRICOS
CONJUNTOS NUMÉRICOS
O conceito de número foi evoluindo ao
longo dos tempos, tendo-se criado novos
números para responder a problemas
entretanto surgidos.
CONJUNTOS NUMÉRICOS
NATURAIS
INTEIROS
RACIONAIS
REAIS
CONJUNTOS NUMÉRICOS
7
NÚMEROS NATURAIS
Estes números foram criados pela
necessidade prática de contar as
coisas da natureza, por isso são
chamados de números naturais.
1
2
3
6
5
4
CONJUNTOS NUMÉRICOS
NÚMEROS NATURAIS
A representação matemática deste conjunto é:
IN = {1, 2, 3, 4, 5, ... }
NÚMEROS INTEIROS
•  Os números naturais não permitiam a resolução de
todas as operações. A subtracção de 3 - 4 era impossível.
•  A ideia do número negativo, aparece na Índia,
associada a problemas comerciais que envolviam
dívidas.
•  A ideia do número zero surgiu também nesta altura,
para representar o nada.
NÚMEROS INTEIROS
A representação matemática deste conjunto é:
Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
NÚMEROS RACIONAIS
Entretanto...surgiu outro tipo de problema:
Como dividir 3 vacas por 2 herdeiros?
Para resolver este tipo de problemas foram criados os
números fracionários. Estes números juntamente com
os números inteiros formam os racionais.
NÚMEROS REAIS
Os pitagóricos ao determinar a medida do
comprimento da diagonal de um quadrado
de lado unitário, não conseguiram encontrar
um número racional para essa medida,
surgindo dessa forma os números reais.
Quando andas de elevador utilizas os
números para subir e descer indicando o
andar a que pretendes chegar, ou seja,
estás a usar alguns elementos do
conjunto dos números inteiros
Apartamento
4
Escritórios
3
Cabeleireiro
2
Restaurante
1
Boutique
0
Ginásio
?
Garagem
?
Lavagem
Automática
?
A senhora que vai ao
cabeleireiro carrega no botão ...
Apartamento
4
Escritórios
3
Cabeleireiro
?2
Restaurante
1
Boutique
0
Ginásio
?
Garagem
?
Lavagem
Automática
?
Qual te parece ser
o andar do ginásio?
Apartamento
4
Escritórios
3
Cabeleireiro
2
Restaurante
1
Boutique
0
Ginásio
-1
?
Garagem
?
Lavagem
Automática
?
E o andar da garagem?
13
Apartamento
4
Escritórios
3
Cabeleireiro
2
Restaurante
1
Boutique
0
Ginásio
-1
Garagem
-2
?
Lavagem
Automática
?
February 6, 2015
E o andar das
lavagens automáticas?
Apartamento
4
Escritórios
3
Cabeleireiro
2
Restaurante
1
Boutique
0
Ginásio
-1
Garagem
-2
Lavagem
Automática
-3
?
REPRESENTAÇÃO NA RETA NUMÉRICA
•  Os números relativos – positivos, negativos ou o zero – podem
ser representados numa recta por meio de pontos.
•  Consideremos uma recta r e marquemos sobre ela um ponto O, a
que chamamos origem.
•  Escolhemos uma unidade de medida e um sentido positivo
(por exemplo da esquerda para a direita).
Desta maneira obtemos um eixo ou reta numérica.
O
-
1
r
+
REPRESENTAÇÃO NA RETA
Se quisermos marcar o ponto A correspondente ao número +5,
contamos 5 unidades para a direita de O.
-
O
+1
+5
+
A
Se quisermos marcar o ponto B correspondente ao número
contamos 3 unidades para a esquerda de O.
-
-3
B
O
+1
-3,
+
REPRESENTAÇÃO NA RETA
O número que corresponde a um ponto do eixo chamamos abcissa
desse ponto.
-
-3
O
+1
+5
A
B
A abcissa de B é -3
A abcissa de A é +5
A origem tem abcissa zero.
+
ORDENAÇÃO
• Quando dispostos sobre um eixo, os números relativos encontram-se
ordenados.
• Se o eixo é horizontal e orientado da esquerda para a direita, um
número é tanto maior quanto mais para a direita se encontrar.
-3
-2
-1
0
1
Cada vez maior
2
3
4
5
ORDENAÇÃO
Vemos, por exemplo, que +5 é maior que +2 e para indicar este facto
escrevemos:
+5>+2
Também se pode dizer que + 2 é menor que + 5 e escrever:
+2<+5
Isto é, se
-3
-2
então
a>b
-1
0
1
b<a
2
•
3
4
5
•
ORDENAÇÃO
Da observação da posição relativa de dois números num eixo resultam
algumas regras para comparar dois números diferentes:
• Qualquer número positivo é maior do que zero.
+ 0,012 > 0
• Zero é maior que qualquer número negativo.
0 > - 35
• Qualquer número positivo é maior do que qualquer negativo.
+1 > - 35
+ 0,5 >; - 100
VALOR ABSOLUTO (OU MÓDULO)
Consideremos agora os pontos A e B, sendo que A tem abcissa + 3 e B
tem abcissa – 2.
-3
-2
-1
0
1
2
B
3
4
5
A
2
3
A distância do ponto A à origem é 3.
A distância do ponto B à origem é 2.
A essa distância chamamos valor absoluto ou módulo.
VALOR ABSOLUTO (OU MÓDULO)
Assim dizemos que o valor absoluto (ou módulo) de +3 é igual a 3 e
escrevemos:
+3 = 3
Portanto, temos ainda que
-2 = 2
Valor absoluto (ou módulo) de um número é a distância à origem do
ponto que representa esse número.
Naturalmente, temos que o valor absoluto de zero é igual a zero:
0 =0
NÚMEROS SIMÉTRICOS
Relativamente à origem da reta, é sempre possível encontrar dois pontos
que se encontram à mesma distância.
-4
-3
-2
-1
0
1
2
3
4
Por exemplo, os pontos de abcissas – 4 e 4 têm a mesma distância à
origem, ou seja,
-4 =
4
Dizemos então que – 4 e 4 são números simétricos.
NÚMEROS SIMÉTRICOS
• Dois números dizem-se simétricos se tiverem sinais contrários
e o mesmo valor absoluto.
Exemplos de números simétricos:
- 0,3 e 0,3
porque
- 0,3 = 0,3
1e -1
porque
1 = -1
Nota que o simétrico do número zero é o próprio número zero:
0 = 0
NÚMEROS SIMÉTRICOS
• Observação
1. De dois números positivos o maior é o que tem maior valor
absoluto (está mais longe da origem).
Exemplos:
+ 0,5 > + 0,1
+ 100 > + 40
2. De dois números negativos o maior é o que tem menor valor
absoluto (está mais perto da origem).
Exemplos:
- 3 > - 50
- 0,01 > - 10
Números Simétricos
Simplificação da escrita
Na reta também se escreve 1, 2, 3,..., em vez de +1,+2,+3,...
-4
-3
-2
-1
0
1
2
3
Também:
+ (+ 8) = + 8
+ (- 8) = - 8
Não é obrigatório escrever o sinal +
4
NÚMEROS SIMÉTRICOS
Na reta numérica o maior dos números encontra-se à direita do menor.
-4
-3
-2
-1
0
-2 é maior que - 4
2 é maior que - 1
1
2
3
-2>-4
ou
- 1 é menor que 2
2>-1
-1<2
> maior
4
< menor